1.4.4. Зрівноваження висот нівелірних мереж методом еквівалентної заміни

Методом еквівалентної заміни можна зрівноважувати не тільки переви­щення, але й висоти точок, числові величини яких називають відмітками.

Нехай маємо мережу з п'яти ходів із двома вузловими точками (рис. 1.4.4).

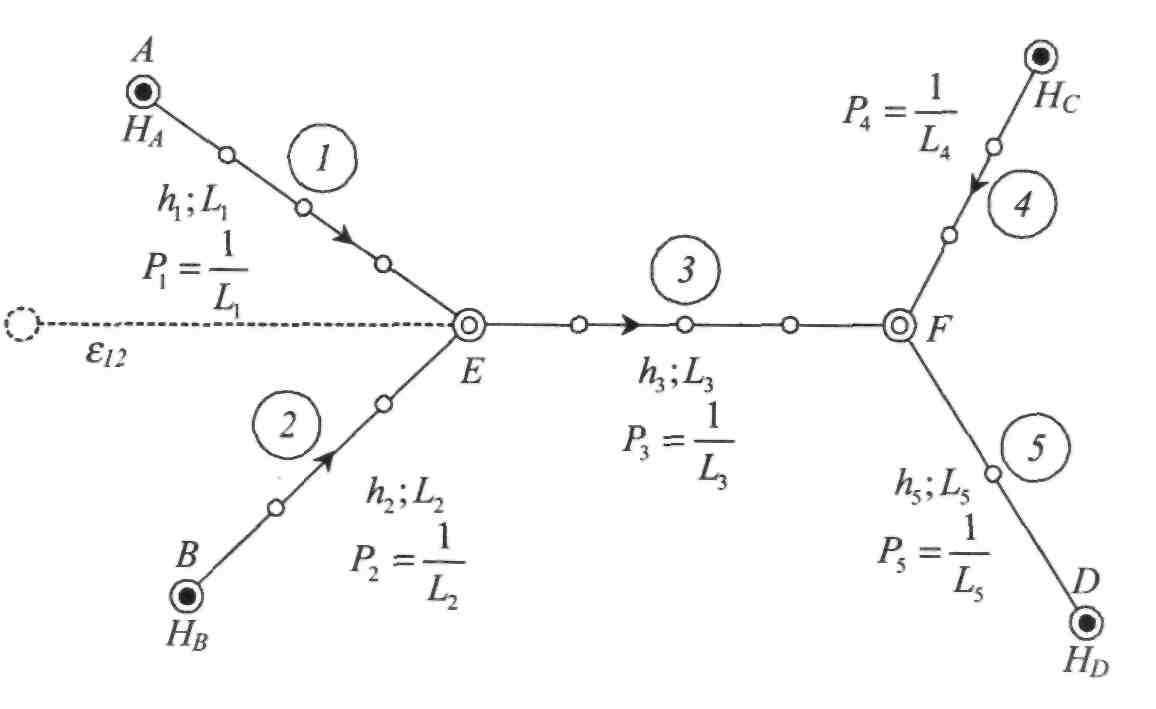
С h,;L₄

Рис. 1.4.4. Нівелірна мережа із двома вузловими точками

Відомі висоти чотирьох реперів, які прийнято називати твердими, оскільки ці репери під час зрівноваження не отримують поправок; відомі також перевищення та ваги ходів. Розглянемо послідовність зрівноваження.

1. Замінимо ходи 1 та 2 еквівалентним ходом є₁₂ і знайдемо висоту вузлової точки Е з двох ходів, точніше, з еквівалентного ходу:

{H_A+h_x)P_l+(H_B+h₂)P₂

(1.4.24)

(1.4.25) (1.4.26)

//іт — -

p_l+p₂

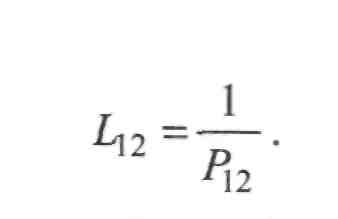
2. Знайдемо вагу та довжину еквівалентного ходу є₁₂:

Р_п=Р_х+Р₂,

3. Визначимо висоту точки F з еквівалентного ходу є_І2 та ходу 3:

Н_пз=Н_п+И₃. (1.4.27)

92

Висотні геодезичні мережі

Тепер, по суті, ми маємо мережу з однією вузловою точкою - F. Знай­демо найімовірніше значення висоти цієї точки:

(1.4.28)

де

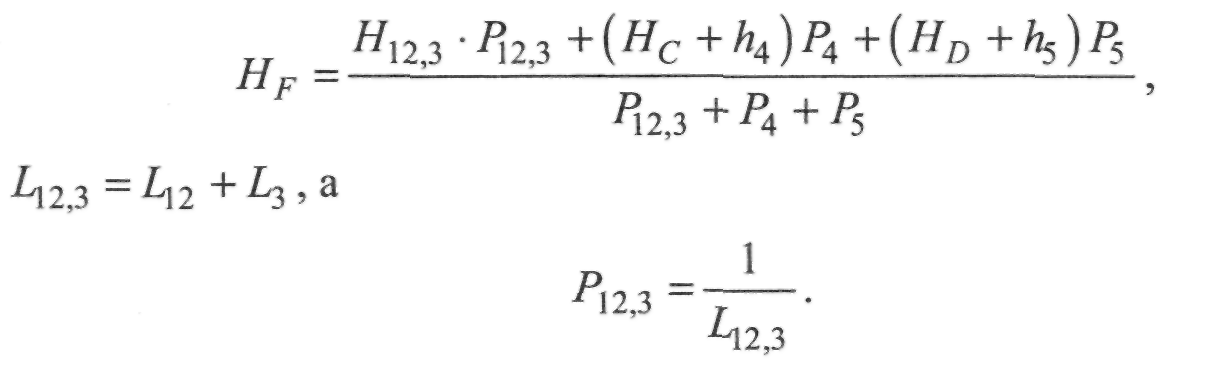(1.4.29)

4. Знаючи зрівноважене значення висоти точки F, знайдемо нев'язки ходів, що сходяться у цій точці:

(1.4.30)

(1.4.31) (1.4.32)

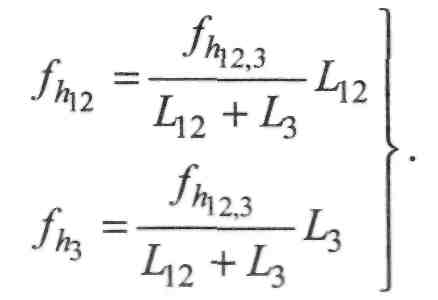
(1.4.33)

5. Розділимо нев'язку /і -і- на нев'язки еквівалентного ходу є₁₂ та ходу З, враховуючи довжини цих ходів:

6. Тепер є можливість розрахувати зрівноважену висоту точки Е - Н_Е з контролем:

(1.4.34)

(1.4.35)

(1.4.36)

7. Залишається знайти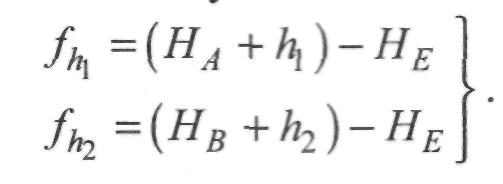 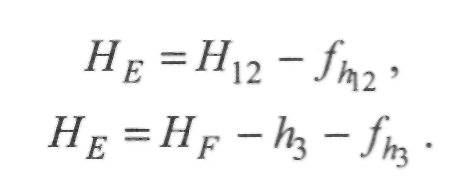нев'язку початкових ходів 1 та 2:

Оцінку точності виконують, як звичайно.

1.4.5. Зрівноваження нівелірних мереж способом послідовних наближень (спосіб вузлів)

Розглянемо застосування цього способу для мережі, що складається із шести ходів, які створюють три вузлові точки (рис. 1.4.5). Відомі перевищення та довжини ходів, висоти трьох реперів, обчислені ваги ходів.

93

Розділ І

Рис. 1.4.5. Нівелірна мережа з трьома вузловими точками

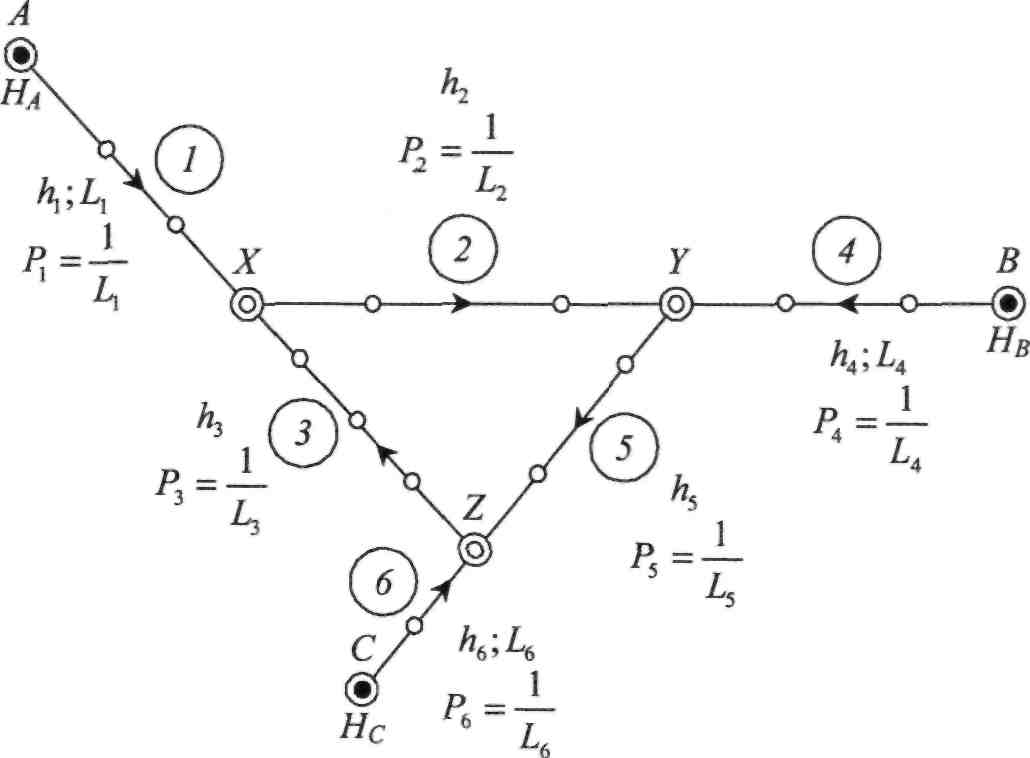
Припустимо, що у якийсь спосіб знайдено висоти вузлових точок X, Y, Z. Але, якщо визначено висоти цих точок, то для кожного ходу можна скласти рівняння похибок.

Врахуємо, що кожен хід має певну вагу. Тому припишемо цим рівнян­ням ваги ходів - Р_і:

(1.4.37)

Як відомо з методу найменших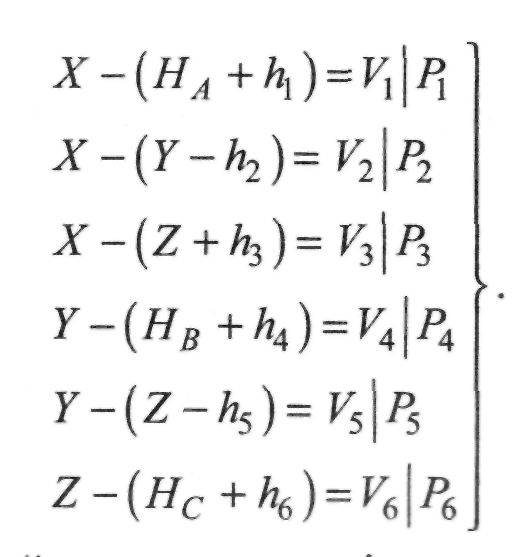 квадратів, якщо рівняння похибок розв'я­зувати згідно з умовою [PW] = min, то приходимо до нормальних рівнянь,

(1.4.38)

яких буде стільки, скільки невідомих. Невідомими фактично є висоти вузлових точок X, Y, Z. Загалом нормальні рівняння для нашої мережі запишуться так:

94

Висотні геодезичні мережі

У нормальних рівняннях прийнято позначати: а,- - коефіцієнти у рів­няннях похибок при першому невідомому (перше невідоме-X), ^-відповідні коефіцієнти при другому невідомому - Y ;c_t- при третьому невідомому - Z. Як видно з (1.4.37), коефіцієнти при X, Y , Z - одиниці, тобто:

а. = 6. = с,- = 1;

/₍- - вільні члени, відомі частини рівнянь:

Перше нормальне рівняння системи (1.4.38) у розгорнутому вигляді запишеться так:

(1.4.39) Розв'яжемо це рівняння відносно невідомого X:

{H_A+h_l)P_l+{Y-h_i)P₂+{Z + h_i)P₃

(1.4.40)

Р_х + Р₂ + Р₃

Аналізуючи (1.4.40), зауважимо, що невідоме X визначається як середнє вагове з трьох ходів, що сходяться у вузлову точку. Тепер, не записуючи інші два нормальні рівняння в розгорнутому вигляді, можемо, за аналогією з (1.4.40), записати формули для знаходження невідомих Y та Z :

_v {X + h_l)P₂+{H_B+h_A)P,+{Z-h₅)P₅

(1.4.41)

(1.4.42)

Оскільки у (1.4.40), (1.4.41), (1.4.42) є невідомі, як у лівій, так і в правій частині, то безпосереднє розв'язання цих рівнянь неможливе. Справді, наприклад, у (1.4.40), в лівій частині невідоме - X, а в правій - невідомі Y та Z. Те саме у двох інших рівняннях. Але ці рівняння можна розв'язувати способом послідовних наближень, тобто способом ітерацій. Для цього спочатку знайдемо наближені значення невідомих висот вузлових точок, викорис­товуючи відомі репери, що розташовані найближче до шуканих:

У рівняння (1.4.40) підставимо наближені значення Y та Z . Знайдемо Х_х із першого наближення. Далі, під час розв'язування рівняння (1.4.41), підставляємо не X , а значення Х_х - із першого наближення. Знайдемо Y_x. Визначаючи Z з (1.4.42), будемо підставляти неХ_пр, Y_np, а Х_х та Y_x. Тоді знайдемо з першого наближення Z_f.

95

Розділ І

Переходимо до другого наближення: визнаючи X, підставляємо у (1.4.40) значення lj, Z( і так далі.

Зазвичай достатньо 3-4 наближень. Ітерацію закінчують, якщо в ос­танньому й передостанньому наближенні значення невідомих однакові. Зрозуміло, що такий метод придатний для мережі зі значною кількістю ходів та вузлових точок. Рівняння для визначення невідомих висот реперів складають безпосередньо зі схеми нівелірної мережі. Тому цей спосіб широко застосо­вується у виробництві. Обчислення виконують на персональних комп'ютерах.