7. Прохождение частицы через потенциальный барьер. Туннельный эффект.

Рассмотрим простейший потенциальный барьер прямоугольной формы (рис. 298, а) для одномерного (по оси х) движения частицы. Для потенциального барьера прямо­угольной формы высоты U и ширины l можем записать

Уравнение Шредингера (217.5) для стационарных состояний для каждой из выде­ленных на рис. 298, а области имеет вид

                                   (221.1)

Общие решения этих дифференциальных уравнений:

                                          (221.2)

                                          

                                          (221.3)

В частности, для области 1 полная волновая функция, согласно (217.4), будет иметь вид

                                 (221.4)

В области 2 решение зависит от соотношений Е>U или Е<U. Физический интерес представляет случай, когда полная энергия частицы меньше высоты потенциального барьера, поскольку при Е<U законы классической физика однозначно не разрешают частице проникнуть сквозь барьер. В данном случае, согласно (221.1), q=i — мнимое число, где

Учитывая значение q и B₃=0, получим решения уравнения Шредингера для трех областей в следующем виде:

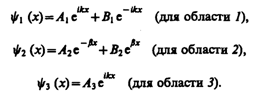                                          (221.5)

Для описания туннельного эффекта используют понятие коэффициента прозрач­ности D потенциального барьера, определяемого как отношение плотности потока прошедших частиц к плотности потока падающих. Можно показать, что

Для того чтобы найти отношение |А₃/А₁|², необходимо воспользоваться условиями непрерывности  и ' на границах барьера х=0 и х=l (рис. 298):

                                                     (221.6)

Эти четыре условия дают возможность выразить коэффициенты A₂, A₃, В₁ и В₂ через А₁. Совместное решение уравнений (221.6) для прямоугольного потенциального барьера дает (в предположении, что коэффициент прозрачности мал по сравнению с единицей)

                                           (221.7)

где U — высота потенциального барьера, Е — энергия частицы, l — ширина барьера, D₀ — постоянный множитель, который можно приравнять единице. Из выражения (221.7) следует, что D сильно зависит от массы т частицы, ширины l барьера и от (U—E); чем шире барьер, тем меньше вероятность прохождения сквозь него частицы.

Для потенциального барьера произвольной формы (рис. 299), удовлетворяющей условиям так называемого квазиклассического приближения (достаточно гладкая форма кривой), имеем

где U=U(x).

8. Квантовый гармонический осциллятор. Уравнение Шредингера. Собственные значения энергии. Основное и возбужденные состояния.

Линейный гармонический осциллятор — система, совершающая одномерное движение под действием квазиупругой силы, — является моделью, используемой во многих задачах классической и квантовой теории. Пружинный, физический и мате­матический маятники — примеры классических гармонических осцилляторов. Потенциальная энергия гармонического осциллятора (см. (141.5)) равна

                                                             (222.1)

где ₀ — собственная частота колебаний осциллятора, т — масса частицы. Зависи­мость (222.1) имеет вид параболы (рис. 300), т. е. «потенциальная яма» в данном случае является параболической.

армонический осциллятор в квантовой механике — квантовый осциллятор — описывается уравнением Шредингера (217.5), учитывающим выражение (222.1) для потенциальной энергии. Тогда стационарные состояния квантового осциллятора определяются уравнением Шредингера вида

                                             (222.2)

 

где Е — полная энергия осциллятора. В теории дифференциальных уравнений до­казывается, что уравнение (222.2) решается только при собственных значениях энергии

                                                     (222.3)

Собственные значения энергии. Рассмотрим систему, состоящую из электрона е, который движется в кулоновском поле неподвижного ядра с зарядом Ze (водородоподобная система). Потенциальная энергия взаимодействия электрона с ядром в такой системе равна

(13.1)

где r — расстояние между электроном и ядром, которое в первом приближении будем считать точечным. Графически функция U(r) изображена жирной кривой на рис. 13.1 а. U(r) с уменьшением r (при приближении электрона к ядру) неограниченно убывает. Уравнение Шрёдингера в этом случае имеет вид

(13.2)

Поле (13.1), в котором движется электрон, является центрально-симметричным, т. е. зависит только от r. Поэтому решение уравнения (13.2) наиболее целесообразно проводить в сферической системе координат r,θ,φ, где оператор Лапласа имеет следующий вид:

Первый случай соответствует свободному электрону (заштрихованная область на рис. 13.1 б), второй — получаемым из уравнения Шредингера собственным значениям энергии

n = 1, 2, 3, …

(13.4)

Таким образом, решение уравнения Шредингера приводит для атома водорода к появлению дискретных энергетических уровней Е₁, Е₂, ..., Е_п, показанных на рис. 13.1 б в виде горизонтальных прямых. 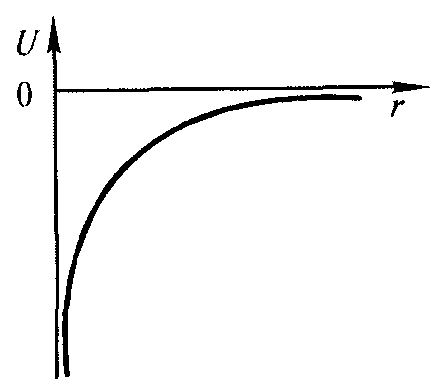а) б) Рис. 13.1 . а - потенциальная энергия U(r) и б - собственные значения энергии Е электрона в атоме водорода. Самый нижний уровень Е₁, отвечающий минимальной возможной энергии, — основной, все остальные (Е_п > Е₁ , п = 2, 3, ...) — возбужденные. При Е < 0 движение электрона является связанным — он находится внутри гиперболической потенциальной ямы. Из рисунка следует, что по мере роста главного квантового числа п энергетические уровни располагаются теснее и при п → ∞ Е_∞ → 0.

9. Атом водорода. Уравнение Шредингера. Собственные значения энергии. Квантовые числа. Вырожденные состояния (состояния с одной энергией и разными другими квантовыми числами, в частности, спиновыми).

Единственный электрон атома водорода находится в состоянии 1s, характеризу­емом квантовыми числами п=1 , l=0, m_l=0 и m_s= ½; (ориентация его спина произвольна).

Собственные функции уравнения (13.2), т. е. ψ-функции, содержат, как выяснилось, три целочисленных параметра — п, ℓ, т:

ψ = ψnℓ m(r θ,φ),

(13.5)

где п называют главным квантовым числом (это то же п, что и в выражении для Е_п). Параметры же ℓ и m — это орбитальное (азимутальное) и магнитное квантовые числа, определяющие по формулам (12.58) и (12.59) модуль момента импульса М и его проекцию М_г. В процессе решения выясняется, что решения, удовлетворяющие естественным условиям, получаются лишь при значениях ℓ, не превышающих (п – 1). Таким образом, при данном п квантовое число ℓ может принимать п значений:

ℓ = 0, 1, 2, …, n – 1.

(13.6)

В свою очередь, при данном ℓ квантовое число т согласно (12.59) может принимать 2ℓ + 1 различных значений:

т = 0, ±1, ±2, ...,± ℓ

(13.7)

Энергия Е_п электрона (13.4) зависит только от главного квантового числа п. Отсюда следует, что каждому собственному значению Е_п (кроме случая п = 1) соответствует несколько собственных функций ψ_{nℓ m}, отличающихся значениями квантовых чисел ℓ и т. Это означает, что электрон может иметь одно и то же значение энергии, находясь в нескольких различных состояниях. Например, энергией Е₂ (п = 2) обладают четыре состояния: ψ₂₀₀, ψ_21-1, ψ₂₁₀, ψ_21+1. Состояния с одинаковой энергией называют вырожденными, а число различных состояний с определенным значением энергии Е_п - кратностью вырождения данного энергетического уровня. Кратность вырождения n-го уровня водородоподобной системы можно определить, учитывая число возможных значений ℓ и т. Каждому из п значений квантового числа ℓ соответствует 2ℓ + 1 значений т. Поэтому полное число N различных состояний для данного п равно

N = = 1 + 3 + 5 + ... + (2п - 1) = п2.

(13.8)

Как будет показано в дальнейшем, это число надо удвоить из-за наличия собственного момента (спина) у электрона. Таким образом, кратность вырождения n-го энергетического уровня

N = 2п2.

(13.9)