39. Под релятиви́стским замедле́нием вре́мени обычно подразумевают кинематический эффект специальной теории относительности, заключающийся в том, что в движущемся телевсе физические процессы проходят медленнее, чем следовало бы для неподвижного тела по отсчётам времени неподвижной (лабораторной) системы отсчёта.
Релятивистское замедление времени проявляется[1], например, при наблюдении короткоживущих элементарных частиц, образующихся в верхних слоях атмосферы под действиемкосмических лучей и успевающих благодаря ему достичь поверхности Земли.
Данный эффект, наряду с гравитационным замедлением времени учитывается в спутниковых системах навигации, например, в GPS ход времени часов спутников скорректирован на разницу с поверхностью Земли[2], составляющую суммарно 38 микросекунд в день
Замедление времени и инвариантность скорости света
Наиболее
наглядно эффект замедления времени
проявляется на примере световых часов,
в которых импульс света периодически
отражается от двух зеркал, расстояние
между которыми равно 
.
Время движения импульса от зеркала к
зеркалу в системе отсчёта, связанной с
часами, равно 
.
Пусть относительно неподвижного
наблюдателя часы двигаются со скоростью 
в
направлении, перпендикулярном траектории
светового импульса. Для этого наблюдателя
время движения импульса от зеркала к
зеркалу будет уже больше.
Световой
импульс проходит в неподвижной системе
отсчёта вдоль гипотенузы треугольника
с катетами 
и 
.
Импульс распространяется с той
же скоростью 
,
что и в системе, связанной с часами.
Поэтому по теореме
Пифагора:
Выражая 
через 
,
получаем формулу замедления времени.
42. Интервал – это расстояние между двумя событиями в пространстве – времени, являющиеся обобщением Евклидова расстояния между точками.
СОБСТВЕННОЕ ВРЕМЯ - время, измеряемое часами, движущимися вместе с рассматриваемым телом, т. е. время в СОБСТВЕННАЯ СИСТЕМА ОТСЧЁТА - система отсчёта, связанная с рассматриваемым телом так, что все точки этого тела покоятся относительно неё. Таким образом, С. с. о. движется вместе с рассматриваемым телом и в общем случае произвольного движения не инерциальна и вращается.
|
Переменим теперь «основную» систему отсчета. Тог да из формул преобразований Лоренца вытекает
|
.Относительность
одновременности событий
является ключевым эффектом СТО,
проявляющимся, в частности, в «парадоксе
близнецов».
Рассмотрим несколько синхронизированных
часов, расположенных вдоль оси 
в
каждой из систем отсчёта. В преобразованиях
Лоренца предполагается, что в момент
времени 
начала
систем отсчёта совпадают: 
.
Ниже изображена такая синхронизация
отсчёта времени (на «центральных» часах)
с точки зрения системы отсчёта 
(левый
рисунок) и с точки зрения наблюдателей
в 
(правый
рисунок):
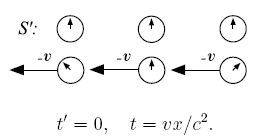
Предположим,
что рядом с каждыми часами в обеих
системах отсчёта находятся наблюдатели.
Положив в преобразованиях Лоренца 
,
получаем 
.
Это означает, что наблюдатели в
системе
, одновременно с
совпадением времени на центральных
часах, регистрируют различные показания
на часах в системе
.
Для наблюдателей, расположенных справа
от точки 
,
с координатами 
,
в момент времени
часы
неподвижной системы отсчёта показывают
«будущее» время: 
.
Наблюдатели
,
находящиеся слева от
,
наоборот, фиксируют «прошлое» время
часов
: 
.
На рисунках выше положение стрелок
символизирует подобную разницу показаний
часов двух систем отсчёта.
Единое «настоящее», то есть часы, синхронно идущие в различных точках пространства, можно ввести только в рамках конкретной инерциальной системы отсчёта. Однако, этого нельзя сделать одновременно для двух различных систем отсчёта.
45. преобразования Галилея - принцип относительности Галилея.
Уравнения, остающиеся неизменными при переходе от одной системы отсчета к другой, называются инвариантными.
Пусть
есть инерциальная система S и движущаяся
относительно ее с постоянной
скоростью
система
S’. Предположим, что известен закон
движения материальной точки в системе
S. Задача нахождения движения этой точки
в системе S’ решается с помощью преобразования
Галилея.
В момент времени
точки
начала координат Ои О’ совпадают
и оси координат (X,Y,Z и X’,Y’,Z’) параллельны
друг другу. Система S’ движется вдоль
оси Z. В момент времени t точка М и системы
координат S и S’ расположены так, как
показано на рисунке.
.
.
.
.
.
В проекциях примет вид
,
,
,
.
В обратной форме
.
А в проекциях
,
,
,
-
эти формулы и являютсяпреобразованием
Галилея.
Преобразование Галилея справедливо в
случае
.
Дифференцируем по времени и получаем нерелятивистский закон сложения скоростей
.
Дифференцируем второй раз по времени и получаем
,
т.е.
.
-
ускорение в системе S;
-
ускорение в системе S’.
Ускорение инвариантно относительно преобразования Галилея.
Принцип относительности Эйнштейна
Законы природы, по которым изменятся состояния физических систем, не зависят от того, к какой из инерциальных систем отсчета относятся эти изменения. Или все физические процессы в инерциальных системах отсчёта протекают одинаково, независимо от того, неподвижна ли система или она находится в состоянии равномерного и прямолинейного движения.
Более общее определение принципа относительности Галилея. Включает в себя не только законы Ньютона, а все физические явления.