
- •Частные производные первого порядка
- •Операции над векторами
- •Линейные операции над матрицами
- •Уравнение прямой с угловым коэффициентом
- •Уравнение прямой в отрезках
- •Уравнение прямой, проходящей через две заданные несовпадающие точки
- •Метод множителей Лагранжа, метод нахождения условного экстремума функции f(X), где , относительно m ограничений , I меняется от единицы до m. Описание метода
- •Обоснование
- •Двумерный случай
- •20.2. Алгоритм решения задач
- •Классическое определение вероятности
- •Полная группа событий
- •Противоположные события
1. Понятия множества, подмножества. Множества конечные и бесконечные. Пустое множество. Мощность множества.
Множество – понимается как определенная совокупность объектов. Объекты – элементы множества. Множество А является подмножеством В, если каждый элемент А является элементом В. Множество называют конечным, если оно содержит конечное число элементов, а если содержит бесконечное число элементов – бесконечное. Пустое – конечное множество с числом элементов=0. Пустое множество – множество не содержащее элементов. Пустое множество – подмножество любого множества. Мощность конечного множества А = количеству его элементов. Два множества равномощны , если между их элементами можно установить взаимооднозначные соответствия.
2. Числовые множества. Операции над множествами (объединение, пересечение, дополнение, декартово произведение) и их свойства.
Множество равнозначное множеству натуральных чисел – счетные или числовые. Операции над множествами: Объединение (сложение) А и В – это множество состоящее из элементов А и В. АUВ. Пересечение (умножение) А и В – это множество, кот. Принадлежит как А так и В. (общие элементы). А В. Разность А и В – это множество состоящее из элементов А, не явл. Элементами В. А\В. Симметрическая разность (дизьюнкция) А и В – множество элементов А и В (ноне обоим вместе, т.е.без общей части).
3. Понятие последовательности. Числовые последовательности и их свойства. Операции над последовательностями.
Числовая последовательность – это числовая функция натурального аргумента. Т.е. функция, область определения которой – множество натуральных чисел, область значения – множество действительных чисел. Последовательность {yn} называют возрастающей, если каждый ее член (кроме первого) больше предыдущего:y1 < y2 < y3 < … < yn < yn+1 < …. Последовательность {yn} называют убывающей, если каждый ее член (кроме первого) меньше предыдущего:y1 > y2 > y3 > … > yn > yn+1 > … .Возрастающие и убывающие последовательности объединяют общим термином – монотонные последовательности. Способы задания последовательности: индуктивный (указывается выражение), геометрический. Операции над последовательностями: {an}±{bn}= {an±bn}=a1±b1,a2±b2,… an±bn
. {an}*{bn}= {an*bn}=a1*b1,a2*b2,… an*bn, {an}:{bn}= {an:bn}=a1:b1,a2:b2,… an:bn
{an}λ= {an λ }=a1 λ,a2 λ,… an λ
4. Ограниченность и монотонность числовой последовательности.
Последовательность аn называется ограниченной снизу, если существует число m для любого n, что аn≥m. Т.е. все члены последовательности неменьше указанного числа. Последовательность ограничена сверху, если есть число М, такое, что для любого аn выполняется аn ≤M. Т.е. М – верхняя граница. Последовательность называют ограниченной, если она ограничена и сверху и снизу. К монотонным последовательностям относятся убывающие, возрастающие, не убывающие, невозрастающие. Последовательность убывающая, если каждый ее член меньше предыдущего. Последовательность – невозрастающая, если ее последующий член не меньше предыдущего. Последовательность называют возрастающей, если каждый ее последующий член больше предыдущего, и не возрастающей, если – не больше предыдущего.
5. Предел числовой последовательности. Теоремы о пределах суммы, произведения, частного последовательностей. С увеличением номера n члены последовательности стремятся к а – пределу последовательности. Число а – предел последовательности {an}, если все члены последовательности отличаются от а сколь угодно мало, когда их номера выше. Последовательность, имеющая предел – сходящаяся, а не имеющая предел – расходящаяся. Если последовательности аn и вn сходятся, то последовательность {an+bn} также сходится. Lim (аn)+lim (bn)= lim (an+bn ). Если последовательности а и в сходятся, то {an*bn} также сходится. Lim (аn)*lim (bn)= lim (an*bn ). Если а и в сходятся, то {an-bn} – сходится. Если а и в сходятся и в≠0, то an/bn – сходится.
6 Предел числовой последовательности. Сходимость последовательности. Необходимое условие сходимости последовательности.
С увеличением номера n члены последовательности стремятся к а – пределу последовательности. Число а – предел последовательности {an}, если все члены последовательности отличаются от а сколь угодно мало, когда их номера выше. Последовательность, имеющая предел – сходящаяся, а не имеющая предел – расходящаяся. Необходимое условие сходимости последовательности:
Если последовательность сходима, то она ограничена. Если последовательность расходится, то она неограниченна.
7. Достаточное условие сходимости последовательности (теорема Вейерштрасса). Теорема о единственности предела сходящейся последовательности.
Теорема Вейерштрасса. Всякая монотонная ограниченная последовательность имеет предел (сходится). Если последовательность возрастает (не убывает), и ограничена сверху, то она имеет предел. Если последовательность убывает (или не возрастает) и ограниченна снизу, то она имеет предел. Если последовательность сходится, то она имеет 1 предел.
8. Числовая последовательность. Примеры числовых последовательностей — арифметическая и геометрическая прогрессии. Определение общего члена и суммы n–первых членов прогрессий.
Числовая последовательность – это числовая функция натурального аргумента. Т.е. функция, область определения которой – множество натуральных чисел, область значения – множество действительных чисел. Примерами числовых последовательностей являются арифметическая и геометрическая прогрессии. Арифметическая прогрессия: d= an+1 –an, an=a1=d(n-1), Sn=(a1+an)/2 *n. Геометрическая прогрессия : q=bn+1/bn , bn=b1*qn+¹, Sn=(bn*g-b1)/q-1.
9. Понятие функции одной переменной. Область определения и область значений функции. Числовые функции.
Если каждому элементу х€Х по какому-то правилу f поставлен в соответствие элемент y€ Y, то говорят, что задано отображение множества Х в множество Y. В том случае, если Х Y – числовые множества, Y – называют функцией.. Отображение числового множества Х в числовое множество Y называется функцией и обозначается y=f(x). Множество Х называют областью определения функции, а множество Y – множеством ее значений ; х называют независимой переменной или аргументом, Y – зависимой переменной или функцией.
10. Элементарные функции, их свойства и графики. Способы задания функции.
Функция
считается заданной, если известно
правило f,
по которому каждому значению аргумента
х можно найти соответствующее значение
y.
Способы задания функции: аналитический
(формулой), графический, табличный,
алгоритмический. Основные виды функций:
Показательные функции: - 3 -
Степенные
функции, Логарифмические функции,
Тригонометрические функции, Обратные
тригонометрические функции. Показательные
функции:
Определение. Функция, заданная
формулой у=ах
(где а>0, а≠1), называется показательной
функцией с основанием а. Область
определения — множество (R) всех
действительных чисел. Область значений
— множество (R+) всех положительных
действительных чисел. При а > 1 функция
возрастает на всей числовой прямой; при
0<а<1 функция убывает. Является функцией
общего вида.
![]() Степенная
функция у=х²
D(x)=R –
функция определена на все числовой оси;
функция принимает положительные значения
на всей области определения; - функция
проходит через начало координат O(0;0).
Функция убывает на промежутке (-∞;0] и
возрастает на промежутке [0;∞). Функция
является четной (симметрична относительно
оси Оу). В зависимости от числового
множителя, стоящего перед х², функция
может быть уже/шире и направлена
вверх/вниз.
Степенная
функция у=х²
D(x)=R –
функция определена на все числовой оси;
функция принимает положительные значения
на всей области определения; - функция
проходит через начало координат O(0;0).
Функция убывает на промежутке (-∞;0] и
возрастает на промежутке [0;∞). Функция
является четной (симметрична относительно
оси Оу). В зависимости от числового
множителя, стоящего перед х², функция
может быть уже/шире и направлена
вверх/вниз.
![]() Логарифмическая
функция у = loga
x обладает следующими свойствами :
Область определения D(x) Î (0; + ∞). Область
значений ( - ∞; + ∞) Функция ни четная,
ни нечетная (общего вида). Функция
возрастает на промежутке (0; + ∞) при a >
1, убывает на (0; + ∞) при 0 < а < 1.
График
функции у = loga
x может быть получен из графика функции
у = ах
с помощью преобразования симметрии
относительно прямой у = х.
Логарифмическая
функция у = loga
x обладает следующими свойствами :
Область определения D(x) Î (0; + ∞). Область
значений ( - ∞; + ∞) Функция ни четная,
ни нечетная (общего вида). Функция
возрастает на промежутке (0; + ∞) при a >
1, убывает на (0; + ∞) при 0 < а < 1.
График
функции у = loga
x может быть получен из графика функции
у = ах
с помощью преобразования симметрии
относительно прямой у = х.
![]()
Тригонометрические функции: Функции y = sin х, у = cos х, у = tg х, у = ctg х называют тригонометрическими функциями.
Функции
у = sin х, у = tg х, у = ctg х нечетные, а функция
у = соs х четная.
Функция
y = sin (х). Область
определения D(x) Î R. Область значений
[ - 1; 1]. Функция периодическая; основной
период равен 2π. Функция нечетная .
Функция возрастает на промежутках [
-π/2 + 2πn; π/2 + 2πn] и убывает на промежутках
[ π/2 + 2πn; 3π/2 + 2πn], n Î Z.
График
функции у = sin (х) изображен на рисунке
11.
![]()
Обратные
тригонометрические функции:
Функции
y = arcsin (х), у = arccos (х), у = arctg (х), у = arcctg (х)
называют обратными тригонометрическими
функциями. Свойства функции y = arcsin (x):
Область определения [−1;1]
Область
значения [−π/2;π/2] . y=arcsin(x)- непрерывная
строго возрастающая функция на D
![]()
![]()
11. Ограниченность и монотонность функций.
Ф ункция f (x) называется возрастающей на промежутке D, если для любых чисел x1 и x2 из промежутка D таких, что x1 < x2, выполняется неравенство f (x1) < f (x2).
Функция f (x) называется убывающей на промежутке D, если для любых чисел x1 и x2 из промежутка D таких, что x1 < x2, выполняется неравенство f (x1) > f (x2). Если существует число C такое, что для любого выполняется неравенство f (x) ≤ C, то функция f называется ограниченной сверху на множестве D. Если существует число c такое, что для любого выполняется неравенство f (x) ≥ c, то функция f называется ограниченной снизу на множестве D.
Функция, ограниченная и сверху, и снизу, называется ограниченной на множестве D. Геометрически ограниченность функции f на множестве D означает, что график функции y = f (x), лежит в полосе c ≤ y ≤ C.
Если функция не является ограниченной на множестве, то говорят, что она не ограничена.
П![]() римером
функции, ограниченной снизу на всей
числовой оси, является функция y = x2.
Примером функции, ограниченной сверху
на множестве (–∞; 0) является функция
y = 1/x.
Примером функции, ограниченной на всей
числовой оси, является функция y = sin x.
римером
функции, ограниченной снизу на всей
числовой оси, является функция y = x2.
Примером функции, ограниченной сверху
на множестве (–∞; 0) является функция
y = 1/x.
Примером функции, ограниченной на всей
числовой оси, является функция y = sin x.
12. Предел функции на бесконечности и в точке. Правила вычисления пределов.
Число
![]() называется
пределом функции
называется
пределом функции
![]() при
при
![]() стремящемся
к бесконечности, если для любого, даже
сколь угодно малого положительного
числа
стремящемся
к бесконечности, если для любого, даже
сколь угодно малого положительного
числа
![]() ,
найдется такое положительное число
,
найдется такое положительное число
![]() (зависящее
от
(зависящее
от
![]() ),
что для всех
таких
что
),
что для всех
таких
что
![]() ,
верно неравенство:
,
верно неравенство:
![]() .
.
Это
предел функции обозначается:
![]() или
или
![]() при
при
![]() .
.
Можно
сформулировать понятие предела при
стремлении
к
бесконечности определенного знака,
т.е. при
![]() и
при
и
при
![]() .
В первом случае основное неравенство:
.
В первом случае основное неравенство:
![]() должно
выполнятся для всех
таких,
что
должно
выполнятся для всех
таких,
что
![]() ,
а во втором – для всех
таких,
что
,
а во втором – для всех
таких,
что
![]() .
.
Предел
функции в точке: Пусть
функция
задана
в некоторой окрестности точки
![]() ,
кроме, быть может, самой точки
.
Определение.
Число
называется
пределом функции
,
кроме, быть может, самой точки
.
Определение.
Число
называется
пределом функции
![]() при
стремящемся
к
(или
в точке
),
если для любого, даже сколько угодно
малого положительного числа
при
стремящемся
к
(или
в точке
),
если для любого, даже сколько угодно
малого положительного числа
![]() ,
найдется такое положительное число
,
найдется такое положительное число
![]() (зависящее
от
),
что для всех
,
не равных
и
удовлетворяющих условию
(зависящее
от
),
что для всех
,
не равных
и
удовлетворяющих условию
![]() ,
выполняется неравенство
,
выполняется неравенство
![]() .
.
Это
предел функции обозначается:
![]() или
при
или
при
![]() .Если
при стремлении
к
переменная
принимает
лишь значения, меньшие
,
или наоборот, лишь значения большие
,
и при этом функция
.Если
при стремлении
к
переменная
принимает
лишь значения, меньшие
,
или наоборот, лишь значения большие
,
и при этом функция
![]() стремится
к некоторому числу
,
то говорят об односторонних
пределах
функции
соответственно
слева
стремится
к некоторому числу
,
то говорят об односторонних
пределах
функции
соответственно
слева
![]() и
справа
и
справа
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
13. Непрерывность функции в точке и на множестве. Непрерывность суммы, произведения и частного непрерывных функций; непрерывность сложной функции.
Функция y=f(x) непрерывная в х0 , если она удовлетворяет условиям: определена в точке х0 (т.е.) существует f(x0) , имеет конечный предел функции при х-х0 , предел равен значению функции в точке х0. Если функции f(x) и q(x) непрерывны в х0, то их сумма f(x)+q(x), произведение, частное являются функциями непрерывными. Если y=f(u) непрерывна в u0 , а u=y(x), то y=f(u(x)) непрерывна в x0.
14. Точка разрыва функции; классификация точек разрыва.
Точка, в которой нарушается непрерывность функции, называется точкой разрыва. Если можно изменить или дополнительно определить f(x) в х0 (т.е.) выбрать число f(x0) так, что измененная или дополненная функция будет непрерывной при х- х0, то эта точка называется устраненной точкой разрыва функции, в противном случае, т.е. когда f(x) разрывная при х=х0 , при любом выборе числа f(x0), значение x0 называется неустраненной точкой разрыва. Точки разрыва функции можно разбить на два типа.
Точка
разрыва x0
функции f(x)
называется точкой
разрыва первого рода,
если существуют оба односторонних
конечных предела
![]() и
и
![]() ,
но они не равны между собой или не равны
значению функции в точке x0,
т.е. f(x0).
Точка разрыва, не являющаяся точкой
разрыва первого рода, называется точкой
разрыва второго рода.
,
но они не равны между собой или не равны
значению функции в точке x0,
т.е. f(x0).
Точка разрыва, не являющаяся точкой
разрыва первого рода, называется точкой
разрыва второго рода.
![]()
![]()
15. Основные свойства непрерывных функций на отрезке: теорема Вейерштрасса о наибольшем и наименьшем значениях функции; теорема о существовании корня; теорема о промежуточном значении функции, теорема об ограниченности функции.
Свойства непрерывных функций.
Сумма, разность и произведение непрерывных в точке х0 функций – есть функция, непрерывная в точке х0.
Частное двух
непрерывных функций
![]() –
есть непрерывная функция при условии,
что g(x)
не равна нулю в точке х0.
–
есть непрерывная функция при условии,
что g(x)
не равна нулю в точке х0.
Суперпозиция непрерывных функций – есть непрерывная функция.
Это свойство может быть записано следующим образом:
Если u = f(x), v = g(x) – непрерывные функции в точке х = х0, то функция v = g(f(x)) – тоже непрерывная функция в этой точке.
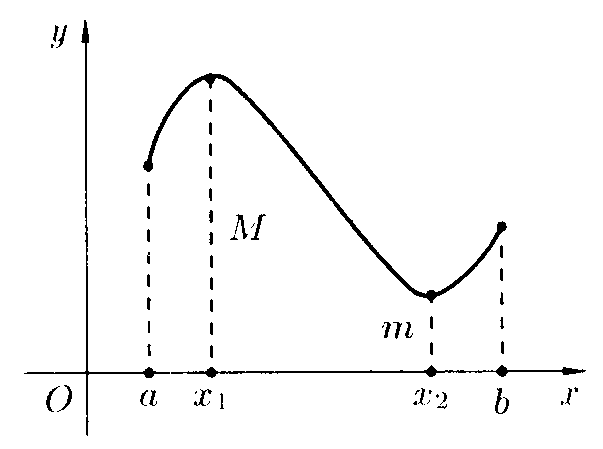 Теорема
Вейерштрасса: Если функция непрерывна
на отрезке, то она достигает на этом
отрезке своего наибольшего и наименьшего
значений.
Теорема
Вейерштрасса: Если функция непрерывна
на отрезке, то она достигает на этом
отрезке своего наибольшего и наименьшего
значений.
Изображенная
на рисунке функция
![]() непрерывна
на отрезке
непрерывна
на отрезке
![]() и
принимает свое наибольшее значение M
в точке
и
принимает свое наибольшее значение M
в точке
![]() ,
а наименьшее m
– в
точке
,
а наименьшее m
– в
точке![]() .
Для любого
.
Для любого
![]() имеет
справедливо неравенство:
имеет
справедливо неравенство:
![]() .
.
Теорема
о промежуточных значениях: Если функция
непрерывна
на отрезке
и
принимает на его концах неравные значения
![]() и
и
![]() ,
то на этом отрезке она принимает все
промежуточные значения между A
и B.
,
то на этом отрезке она принимает все
промежуточные значения между A
и B.
Г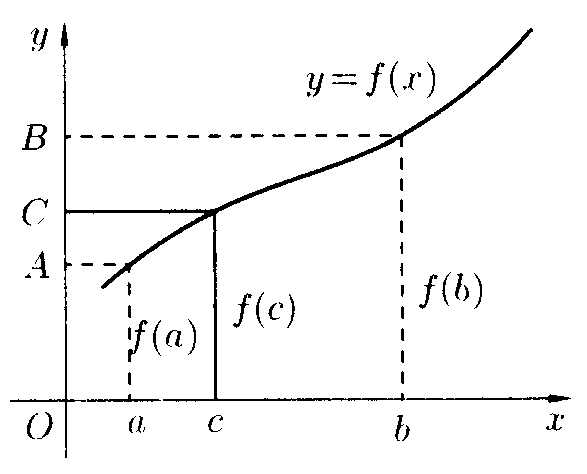 еометрически
теорема показана на рисунке.
еометрически
теорема показана на рисунке.
Для
любого числа С, заключенного между A
и B,
найдется точка с внутри этого отрезка
такая, что
![]() .
Прямая y=C
пересечет график функции по крайней
мере в одной точке.
.
Прямая y=C
пересечет график функции по крайней
мере в одной точке.
Конец формы
![]()
16. Определение производной функции одной переменной. Геометрический, механический и экономический смысл производной.
Производной
функции
называется предел отношения приращения
функции к приращению аргумента.
Пусть функция y=f(x)
определена в точке x
и в некоторой ее окрестности. Дадим
аргументу x
приращение x,
такое, чтобы не выйти из указанной
окрестности. Найдем соответствующее
приращение функции y
и составим отношение. Если существует
предел этого отношения при x0,
то указанный предел называют производной
функции y=f(x)
в точке x
и обозначают f
`(x).
![]()
Производная функции f в точке x0 есть скорость изменения функции в этой точке.. геометрическое толкование производной. Производная функции f в точке x0 определяется тангенсом угла наклона касательной, проведенной к графику функции f в точке х=x0. экономический смысл производной. Производительность труда есть производная от объема произведенной продукции по времени. Производная выступает как интенсивность изменения некоторого экономического объекта (процесса) по времени или относительно другого исследуемого фактора.
17. Связь между свойствами непрерывности и дифференцируемости функции.
Если функция дифференцируема в некоторой точке, то в этой точке функция непрерывна. Обратное утверждение не верно.
![]() - непрерывна, но не
является дифференцируемой в точке х=0
т.к. к ней нет касательной.
- непрерывна, но не
является дифференцируемой в точке х=0
т.к. к ней нет касательной.
18. Производные элементарных функций. Основные правила дифференцирования. Производная второго порядка.
Если следовать определению, то производная функции в точке — это предел отношения приращения функции Δy к приращению аргумента Δx:
![]()
Но попробуйте посчитать по этой формуле, скажем, производную функции f(x) = x2 + (2x + 3) · ex · sin x. Если все делать по определению, то через пару страниц вычислений вы просто уснете. Поэтому существуют более простые и эффективные способы.Для начала заметим, что из всего многообразия функций можно выделить так называемые элементарные функции. Это относительно простые выражения, производные которых давно вычислены и занесены в таблицу. Такие функции достаточно просто запомнить — вместе с их производными.Производные элементарных функций
Элементарные функции — это все, что перечислено ниже. Производные этих функций надо знать наизусть. Тем более что заучить их совсем несложно — на то они и элементарные.
Итак, производные элементарных функций:
Название |
Функция |
Производная |
Константа |
f(x) = C, C ∈ R |
0 |
Степень с рациональным показателем |
f(x) = xn |
n · xn − 1 |
Синус |
f(x) = sin x |
cos x |
Косинус |
f(x) = cos x |
− sin x (минус синус) |
Тангенс |
f(x) = tg x |
1/cos2 x |
Котангенс |
f(x) = ctg x |
− 1/sin2 x |
Натуральный логарифм |
f(x) = ln x |
1/x |
Произвольный логарифм |
f(x) = loga x |
1/(x · ln a) |
Показательная функция |
f(x) = ex |
ex |
Применяя общий способ нахождения производной с помощью предела можно получить простейшие формулы дифференцирования. Пусть u=u(x),v=v(x) – две дифференцируемые функции от переменной x.
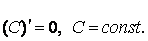
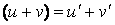 (справедлива
для любого конечного числа слагаемых).
(справедлива
для любого конечного числа слагаемых).
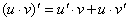 .
.
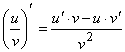 .
.
а)
![]() .
.
б)
![]() .
.
Когда мы дифференцируем функцию, каждой точке этой функции мы ставим в соответствие некоторое число – ее производную в данной точке. Таким образом, производная функции также является функцией.
Если
функция
![]() дифференцируема,
то ее производную называют второй
производной от
f и
обозначают
дифференцируема,
то ее производную называют второй
производной от
f и
обозначают
![]() :
:
![]()
Вторая
производная от параметрической функции
x =
x (
t )
и y =
y (
t )
задается формулой:
![]()
19. Правило Лопиталя; раскрытие неопределенностей различных видов.
метод нахождения
пределов
функций,
раскрывающий
неопределённости
вида 0 / 0
и
![]() .
Обосновывающая метод теорема утверждает,
что при некоторых условиях предел
отношения функций
равен пределу отношения их производных.
.
Обосновывающая метод теорема утверждает,
что при некоторых условиях предел
отношения функций
равен пределу отношения их производных.
Если существует
![]() ,
,
тогда
существует
![]() .
.
20. Необходимый и достаточный признаки возрастания (убывания) функции.
Необходимые признаки: если дифференцируемая функция возрастает на некотором промежутке, то производная этой функции неотрицательна. Если дифференцируемая функция убывает на некотором промежутке, то производная этой функции не положительна.
Достаточный признак возрастания: Если производная дифференцируемой функции «+» внутри некоторого промежутка, то функция возрастает на этом промежутке. Если производная дифференцируемой функции «-» внутри некоторого промежутка, то функция убывает на этом промежутке.
21. Необходимое и достаточные условия экстремума функции.
Наличие max и min в отдельной точке промежутка Х не означает, что в этой точке функция приобретает наибольшее или наименьшее значение, т.е. глобальный max и min. Необходимые условия существования экстремума: Теорема Ферма: если точка х0 является точкой экстремума функции и в этой точке существует производная, то эта производная =0. Первое достаточное условие экстремума: если функция непрерывна, имеет производную в окрестностях точки х0 и при переходе через точку х0 меняет знак с «+» на «-», то х0 - точка max. Если при переходе черех точку производная меняет знак с «-» на «+», то х0 – min. Если производная при переходе через точку не меняет знак, то в этой точке нет экстремума.
22. Выпуклость и вогнутость графика функции. Достаточное условие выпуклости (вогнутости) графика функции.
Функция называется выпуклой вниз (вогнутой) на промежутке, если для любых 2-х точек Х1 и Х2 выполняется неравенство f(x1+x2)≤(f(x1)+f(x2))/2. Функция называется выпуклой вверз на промежутке, если для любых x1иx2 выполняется условие f(x1+x2)≥(f(x1)+f(x2))/2. График функции y=f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале.
График функции y=f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале. Функция выпукла вниз (вверх)тогда и только тогда, когда ее первая производная на этом промежутке монотонно возрастает.
23. Точки перегиба функции. Необходимое и достаточное условия перегиба графика функции. Асимптоты графика функции.
Точкой перегиба графика непрерывной функции называется точка, разделяющая интервалы, в которых функция выпукла вниз, вверх. Необходимое условие перегиба: f’’(x) дважды дифференцируемая функция в точке перегибе х0 =0. Достаточное условие перегиба: если f’’(x) дважды дифференцируемая функция при переходе через некоторую точку меняет свой знак, то х0 - есть точка перегиба. Асимптомой графика функции называется прямая, обладающая тем свойством, что расстояние от точки (x; f(x)) до этой прямой стремится к 0 при неограниченном удалении. Асимптому нужно искать в точках разрыва или на концах ее области определения.
24. Определение дифференциала функции. Теорема о единственности дифференциала функции.
Дифференциал
– величина, пропорциональная приращению
независимой переменной и отличающаяся
от приращения функции на бесконечно
малую функцию высшего порядка.
∆y=f(x+∆x)-f(x)
(приращение функции). Дифференциалом
функции
![]() (обозначается
через
(обозначается
через
![]() )
называется следующее выражение:
)
называется следующее выражение:
![]()
где dx -- дифференциал x при условии, что функция имеет производную.
Теорема о единстве дифференциала: Данная функция может иметь только 1 дифференциал.
25. Связь дифференциала функции с производной. Свойства дифференциала.
Если функция имеет дифференциал, то она имеет и производную. Следствие: если функция имеет производную, то она имеет и дифференциал. Дифференциал функции = произведению производной на приращение независимой переменной. dy= y’ ∆x. Дифференциал функции обладает свойствами, аналогичными свойствам производной.
Дифференциал постоянной равен нулю: dc = 0, с = const.
Дифференциал суммы дифференцируемых функций равен сумме дифференциалов слагаемых: d(u+v)=du + dv Следствие. Если две дифференцируемые функции отличаются постоянным слагаемым, то их дифференциалы равны d(u+c) = du (c= const).
Дифференциал произведения двух дифференцируемых функций равен произведению первой функции на дифференциал второй плюс произведение второй на дифференциал первой: d(uv) = udv + vdu. Следствие. Постоянный множитель можно выносить за знак дифференциала d(cu) = cdu (с = const).
Дифференциал частного u/v двух дифференцируемых функций и = и(х) и v = v(x) определяется формулой
![]()
26. Понятие производственной функции одной или нескольких переменных. Факторные модели производственно-экономических систем.
Производная функции – это функция, независимая переменная которой принимает значение использованного ресурса (фактора производства), ее независимая переменная – значение объемов выпускаемой продукции. Производная функции называется одноресурсной или однофакторной, ее область определения – множество неотрицательных чисел. Производные могут иметь разные области использования. Принцип – «затраты-выпуск» может быть реализован как микро-, так и на макро-экономическом уровне. производная может быть использована для описания отношений между годовыми затратами труда в масштабе региона или страны и годовым конечным выпуском продукции.
27. Средние, приростные и предельные показатели использования факторов производства в однофакторной модели.
Функция предложения заключается в общем виде в том, чтобы связать производство с потреблением, продажу товаров с их покупкой. Реагируя на возникающий спрос, производство начинает увеличивать выпуск товаров, улучшать их качество и уменьшать издержки, а тем самым увеличивать общий объем предложений на рынке. При изучении спроса различают реализованный (удовлетворенный), неудовлетворенный и формирующийся спрос. Функции полезности: одномерные и многомерные, аудитивные, порядковые и качественные, мультикативные, монотонные и немонотонные, линейные и нелинейные, одночисленные и поличисленные.
28. Приростная и предельная эластичности по его фактору
ПРЕДЕЛЬНЫЕ И ПРИРОСТНЫЕ ВЕЛИЧИНЫ В ЭКОНОМИКЕ [differential values in economics] — предельная величина характеризует не состояние (как суммарная или средняя величины), а процесс, изменение. Поскольку в экономике большинство процессов, рассматриваемых как непрерывные (напр., рост производства или изменение его эффективности), являются функциями ряда аргументов (факторов), то предельные величины здесь обычно выступают как частные производные результативных показателей процесса по каждому из факторов.
Экономический смысл предельных величин состоит в том, что их можно использовать для принятия оптимальных решений с помощью методов дифференциального исчисления. Тогда, в частности, нахождение оптимума основывается на элементарных правилах: если при анализе функции первая производная равна нулю, это означает экстремум функции и, следовательно, возможный ее оптимум.
29. Показатели эффективности и эластичности для линейной и степенной производственной функции.
Способность спроса и предложения адаптироваться к изменившимся условиям рынка называется эластичностью (с точки зрения математики – эластичность – это отношение относительного прироста функции к относительному приросту независимой переменной). Зависимость объема спроса на товар от изменения цены на него называют эластичностью спроса по цене. Наиболее общее определение эластичности — отношение относительного приращения функции к относительному приросту независимой переменной.
![]()
Для рассматриваемых нами функций спроса и предложения такими независимыми переменными могут быть цены данного или других товаров, уровень доходов, издержек и т.д.
30. Функции полезности, спроса, предложения и их показатели эффективности и эластичности.
Наиболее общее определение эластичности — отношение относительного приращения функции к относительному приросту независимой переменной.
Для рассматриваемых нами функций спроса и предложения такими независимыми переменными могут быть цены данного или других товаров, уровень доходов, издержек и т.д.
Коэффициент эластичности показывает степень количественного изменения одного фактора (например, объема спроса или предложения) при изменении другого (цены, доходов или издержек) на1%.
Эластичность спроса или предложения вычисляется как отношение процентного изменения величины спроса (предложения) к процентному изменению какой-либо детерминанты.
Детерминанты — это факторы оказывающие воздействие на спрос или предложение.
31. Первообразная и неопределенный интеграл. Основные свойства неопределенного интеграла.
Пусть функция f(x) задана на некотором интервале R. Если найдется функция F(x), что при всех x€R, имеет место равенство F’(x)= f(x), то функция F(x)называется первообразной для функции f(x). Нахождение первообразной – это операция, обратная к операции вычисления производной. Неопределенный интеграл – множество первообразных функций. f(x) (ʃ f(x)dx). Свойства неопр интеграла: dʃ f(x)dx= f(x)dx, ʃF’(x)dx=F(x)+c.
32. Таблица простейших неопределенных интегралов. Основные методы интегрирования: замена переменной и интегрирование по частям.
Пользуясь тем, что интегрирование есть операция, обратная дифференцированию, нетрудно получить таблицу простейших интегралов.
Обращая формулы дифференцирования, получим:

Для вычисления неопределенного интеграла мы должны, если это возможно, привести его к табличным интегралам. Рассмотрим основные приемы интегрирования.
I. Метод
разложения.
Пусть
![]() .
Тогда на основании свойства неопределенного
интеграла имеем
.
Тогда на основании свойства неопределенного
интеграла имеем
![]() ,
,
причем
слагаемые
![]() и
и
![]() стараются
подобрать так, чтобы интегралы от них
находились непосредственно.
стараются
подобрать так, чтобы интегралы от них
находились непосредственно.
II. Метод
подстановки (метод введения новой
переменной).
Данный метод состоит в том, что в интеграле
![]() ,
нахождение которого затруднительно,
вводят новую переменную t,
связанную с переменной x
соотношением
,
нахождение которого затруднительно,
вводят новую переменную t,
связанную с переменной x
соотношением
![]() ,
,
где
![]() –
непрерывная строго монотонная функция,
имеющая непрерывную производную
–
непрерывная строго монотонная функция,
имеющая непрерывную производную
![]() на
некотором интервале изменения
на
некотором интервале изменения
![]() ,
после чего получают
,
после чего получают
![]() .
.
При
этом стремятся подобрать такую подстановку
,
чтобы интеграл в правой части этого
равенства был табличным или путь его
нахождения был ясен. После того как этот
интеграл найден возвращаются к
первоначальной переменной с помощью
обратной подстановки
![]() .
.
Заметим, что на практике часто встречаются интегралы вида
![]() (57)
(57)
или
интегралы, которые сводятся к такому
виду. Подведем в этом интеграле множитель
![]() под
знак дифференциала, а затем произведем
подстановку
под
знак дифференциала, а затем произведем
подстановку
![]() .
В результате получим формулу подстановки
в неопределенном интеграле
.
В результате получим формулу подстановки
в неопределенном интеграле
![]() ,
,
которая упрощает подынтегральное выражение и во многих случаях способствует быстрому получению окончательного результата.
Частым случаем интеграла вида (57) является интеграл
![]() .
.
Если
![]() –
первообразная функции
–
первообразная функции
![]() на
некотором интервале
на
некотором интервале
![]() ,
то, пользуясь подстановкой
,
то, пользуясь подстановкой
![]() ,
получаем
,
получаем
![]() .
(58)
.
(58)
III.
Метод интегрирования по частям.
Пусть
![]() и
и
![]() –
непрерывно дифференцируемые функции
аргумента
–
непрерывно дифференцируемые функции
аргумента
![]() .
На основании формулы дифференциала
произведения имеем
.
На основании формулы дифференциала
произведения имеем
![]() .
.
Отсюда
![]() .
.
Интегрируя
обе части данного равенства, получим
![]() или
окончательно (так как
или
окончательно (так как
![]() )
)
![]() .
(59)
.
(59)
Эта
формула называется формулой интегрирования
по частям. Она показывает, что интеграл
![]() приводится
к интегралу
приводится
к интегралу
![]() ,
который может оказаться более простым,
чем исходный, или даже табличным.
,
который может оказаться более простым,
чем исходный, или даже табличным.
К интегралам, которые находятся по формуле (59) относятся, например, интегралы вида
![]() ,
,
где
![]() –
многочлен;
–
многочлен;
![]() –
одна из следующих функций:
–
одна из следующих функций:
![]()
![]() .
Чтобы свести в этом случае интеграл к
табличному, надо последовательно
применять формулу (59) столько раз, какова
степень многочлена
,
причем в первый раз за
выбрать
и
за
.
Чтобы свести в этом случае интеграл к
табличному, надо последовательно
применять формулу (59) столько раз, какова
степень многочлена
,
причем в первый раз за
выбрать
и
за
![]() выбрать
выбрать
![]() .
.
33. Определенный интеграл. Формула Ньютона–Лейбница. Связь определенного и неопределенного интегралов.
Пусть
функция f(x)
непрерывна на отрезке [a,b]
, F(x)
– ее первообразная при x€[a,b].
Под определенным интегралом ʃaͩ
f(x)dx
от данной непрерывной функции на данном
отрезке [a,b]
понимается соответствующее приращение
ее первообразной F(b)-F(a).
Формальная разница между определенным
и неопределенным интегралом – определенный
интеграл – это число, а неопределенный
– это свойство функции. Значение
определенного интеграла может быть
вычислено по формуле Ньютона-Лейбница
![]() =
=![]() ,
здесь символ
,
здесь символ
![]() означает,
что из значения
означает,
что из значения
![]() при
верхнем пределе b нужно вычесть значение
при нижнем пределе a ,
—
первообразная
функция для
при
верхнем пределе b нужно вычесть значение
при нижнем пределе a ,
—
первообразная
функция для
![]() .
.
34. Основные свойства определенного интеграла (общие свойства, свойства аддитивности, линейности, монотонности).
Общие свойства: величина определенного интеграла не зависит от обозначения переменной интегрирования ʃaͩ f(x)dx = ʃaͩ f(t)dt . Определенный интеграл с одинаковыми пределами интегрирования =0 ʃaͣ f(x)dx = F(a)-F(a)=0. при перестановке пределов интегрирования определенный интеграл меняет знак. ʃaͩ f(x)dx =- ʃdͣͩ f(x)dx .
Свойство
аддитивности если промежуток интеграла
разбит на конечное число промежутков,
то определенный интеграл равен сумме
опр. интегралов взятых по его частичным
промежуткам.
![]()
Свойство линейности. Постоянный множитель можно выносить за знак определенного интеграла. . ʃaͩ Аf(x)dx=А. ʃaͩ f(x)dx, Определенный интеграл от алгебраической суммы равен той же алгебраической сумме определенных интегралов. . ʃaͩ f(x) +q(x) –h(x)dx= ʃaͩ f(x)dx+ ʃaͩ q(x)dx- ʃaͩ h(x)dx.
Свойство монотонности. Если подинтегральная функция определенного интеграла непрерывна и неотрицательна, а верхний предел > нижнего и не равен ему, то определенный интеграл тоже неотрицателен.
35. Приложения определенного интеграла: вычисление площадей плоских фигур, объёма тела вращения. Приложения определенного интеграла в экономических задачах.
С точки зрения геометрии определенный интеграл – это ПЛОЩАДЬ. То есть, определенному интегралу (если он существует) геометрически соответствует площадь некоторой фигуры.
Рассмотрим на плоскости Оху фигуру, ограниченную графиком непрерывной и положительной функции f(x) на отрезке [а, b], отрезком [а, b] и вертикальными прямыми х = а и х = b (рис. 7.2). Эту фигуру будем называть криволинейной трапецией.
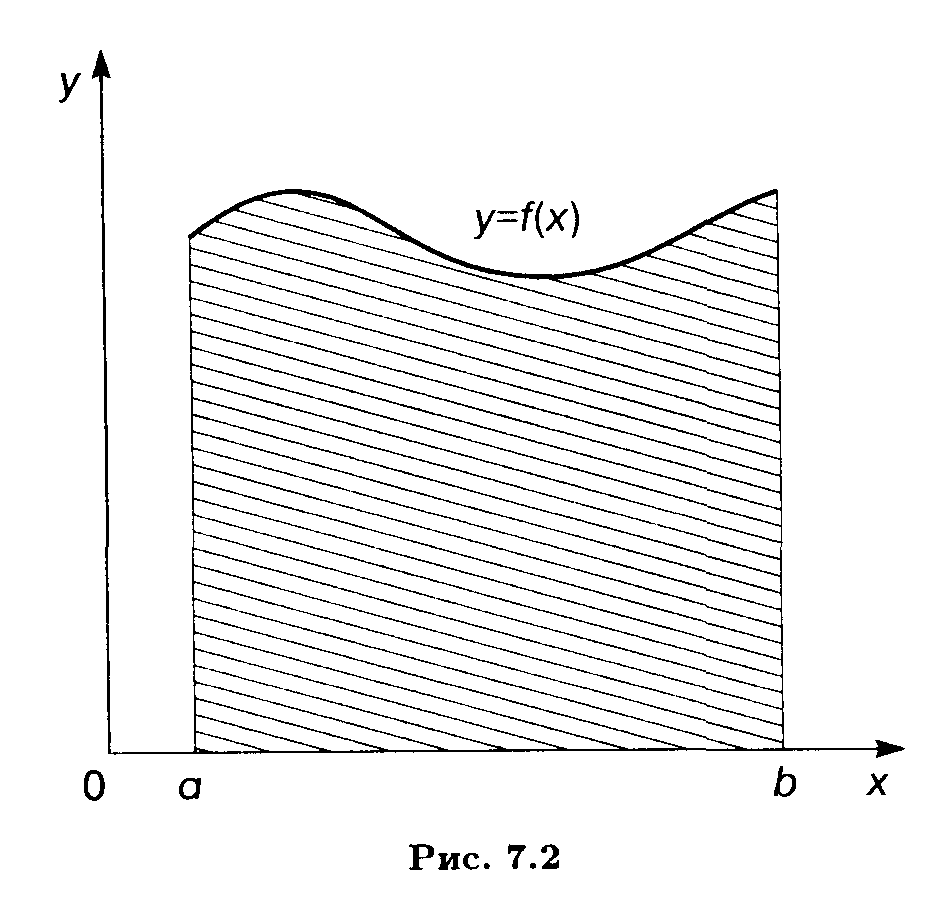
Величина площади криволинейной трапеции равна определенному интегралу от функции f(x) на отрезке [а, b]:
![]()
Пусть вокруг оси Ох вращается криволинейная трапеция, ограниченная непрерывной линией у = ƒ(х) 0, отрезком а ≤ x ≤ b и прямыми х = а и х = b (см. рис. 190). Полученная от вращения фигура называется телом вращения. Сечение этого тела плоскостью, перпендикулярной оси Ох, проведенной через произвольную точку х оси Ох (х [а; b]), есть круг с радиусом у= ƒ(х). Следовательно, S(x)=πy2.
П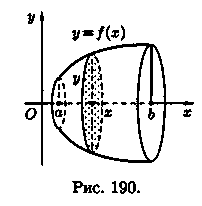 рименяя
формулу (41.6) объема тела по площади
параллельных сечений, получаем
рименяя
формулу (41.6) объема тела по площади
параллельных сечений, получаем
![]()
Если криволинейная трапеция ограничена графиком не прерывной функции х=φ(у) ≥ 0 и прямыми х = 0, у = с,
у = d (с < d), то объем тела, образованного вращением этой трапеции вокруг оси Оу, по аналогии с формулой (41.7), равен
![]()
36. Понятие функции нескольких переменных. График функции двух переменных. Линии уровня функции двух переменных.
Пусть каждой точке М из множества точек {М} по какому-либо закону ставится в соответствие некоторое число и из числового множества U. Тогда будем говорить, что на множестве {М} задана функция и = f(M). При этом множества {М} и U называются соответственно областью определения (задания) и областью изменения функции f(M).
Как известно, функция одной переменной у = f(x) изображается на плоскости в виде линии. В случае двух переменных область определения {Мп} функции z = f(x, y) представляет собой некоторое множество точек на координатной плоскости Оху (рис. 8.1). Координата z называется аппликатой, и тогда сама функция изображается в виде некоторой поверхности в пространстве E3. Аналогичным образом функция от т переменных
![]()
Понятие линии уровня широко используется прежде всего в геодезии, картографии, при составлении синоптических карт, а также при описании различных физических полей (температура, давление и пр.).
Определение 2. Линией уровня функции двух переменных z = f(x, y) называется плоская кривая, получаемая при пересечении графика этой функции плоскостью z = С, где С — постоянная величина, параллельной координатной плоскости Оху. Таким образом, можно сказать, что линии уровня функции z = f(x, у) — это семейство кривых на координатной плоскости Оху, описываемое уравнениями вида
![]()
37. Полное и частные приращения функции нескольких переменных. Предел и непрерывность функции.
Пусть дана функция Z=f(x,y), совокупность значений x,y будем называть точкой. Дадим приращение ∆х переменной х, а y оставим без изменения. ∆f(x,y)=f(x+∆x,y)-f(x,y) –частное приращение функции по переменной х. ∆y f(x,y)=f(x,y+∆y)-f(x,y) – частное приращение по y.
∆f(x,y)=f(x+∆x,y+∆y)-f(x,y) – полное приращение.
Функция называется неприращенной в точке, если функция определена в данной точке и эта точка является предельной для области существования функции. И если бесконечно малым приращение переменных соответствует бесконечно малые приращения функции.
38. Частные производные первого и второго порядка функции нескольких переменных, их определения и правила вычисления.
Частные производные первого порядка
Пусть функция двух переменных z = f(x, у) определена в некоторой окрестности точки М(x, у) евклидова пространства Е2. Частная производная функции z = f(x, у) по аргументу x является обыкновенной производной функции одной переменной х при фиксированном значении переменной у и обозначается как
![]()
Аналогичным образом определяется частная производная функции f(x, у) по переменной у в точке М, обозначаемая как
![]()
Функция, имеющая частные производные, называется дифференцируемой.
Совершенно аналогично определяются частные производные функций трех и более переменных. Частная производная функции нескольких переменных характеризует скорость ее изменения по данной координате при фиксированных значениях других координат.
39. Дифференциал функции нескольких переменных. Достаточное условие дифференцируемости функции.
Пусть функция z =ƒ (х; у) определена в некоторой окрестности точки М(х;у). Составим полное приращение функции в точке М:
![]()
Функция z = ƒ (х; у) называется дифференцируемой в точке М(х; у), если ее полное приращение в этой точке можно представить в виде
![]()
где а = а(Δх, Δу)→0 и β=β(Δх,Δу)→0 при Δх→0, Δу→0. Сумма первых двух слагаемых в равенстве (44.1) представляет собой главную часть приращения функции.
Главная часть приращение функции z=ƒ(х;у), линейная относительно Δх и Δу, называется полным дифференциалом этой функции и обозначается символом dz:
dz=A*Δx+B*Δy. (44.2)
Выражения А•Δх и В•Δу называют частными дифференциалами. Для независимых переменных х и у полагают Δх=dx и Δу=dy. Поэтому равенство (44.2) можно переписать в виде
dz=Adx+Bdy. (44.3)
(достаточное условие дифференцируемости функции). Если функция z = ƒ(х;у) имеет непрерывные частные производные z'x и z'y в точке М(х;у), то она дифференцируема в этой точке и ее полный дифференциал выражается формулой (44.5).
40. Необходимое условие существования полного дифференциала функции двух переменных
(необходимое условие дифференцируемости функции). Если функция z = ƒ(х;у) дифференцируема в точке М(х;у), то она непрерывна в этой точке, имеет в ней частные производные dz/dx и dz/dy, причем dz/dx = А, dz/dy = В.
41. Экстремум функции двух переменных. Необходимое и достаточные условия экстремума функции двух переменных.
Пусть функция z = f(x, y) определена на множестве {М}, а М0 (x0, у0) — некоторая точка этого множества.
Определение. Функция z = f(x, у) имеет в точке М0 локальный максимум (минимум), если существует такая окрестность точки M0, принадлежащая {М}, что для любой точки М(х, у) из этой окрестности выполняется неравенство f(M) ≤ f(M0) (f(М) ≥ f(М0)); для случая функции трех и более переменных локальный экстремум определяется аналогично.
Согласно данному определению локального экстремума (минимума или максимума) полное приращение функции z = f(M) — f(М0) удовлетворяет одному из условий в окрестности точки M0:
Δz ≤ 0, если M0 — точка локального максимума;
Δz ≥ 0, если M0 — точка локального минимума.
. Если функция z = f(x, у) имеет в точке M0 (x0, y0) локальный экстремум и частные производные первого порядка, то все эти частные производные равны нулю:
![]()
Пусть в точке М0(х0, у0) возможного экстремума функции и = f(x, у) и в некоторой ее окрестности все вторые частные производные этой функции непрерывны. Тогда если
![]()
то функция и = f(x, y) имеет в точке М0 локальный экстремум: минимум при а11 < 0 и максимум при а11 > 0. Если же а11а22 — a122 ≤ 0, то данная функция не имеет локального экстремума в точке M0.
42. Глобальный экстремум функции; теорема Вейерштрасса.
43. Метод наименьших квадратов; построение эмпирических формул способом наименьших квадратов (линейная зависимость).
Пусть S зависит от t: S=f(t), причем функция, описывающая зависимость, точно неизвестна, известны только значения этой функции в отдельных точках, т.е. данные заданы в таблице. Задача состоит в том, чтобы вывести аналитическое отношение, которое описывает зависимость S=f(t).,такая зависимость называется трендом. Простейший подход к решению этой задачи состоит в том, что : заранее предполагается, что функция g, описывающая зависимость S=f(t), имеет какой то определенный вид, будем рассматривать функцию линейную, т.е. решим задачу об отыскивании линейного тренда. S≈g(t)=a+bt, где a b -неизвестные постоянные коэффициенты. A и b находятся исходя из следующего условия: сумма квадратов отклонений трендовых значений в точке t от соответствующих заданных значений переменной S должна быть минимальной. F(a,b)= ∑(a+bt-S)² >0
ϑф =2∑(a+bt-S)=0 ϑф =2∑(a+bt-S)=0
ϑа ϑb
44. Средние, приростные и предельные показатели использования факторов производства в двухфакторной модели.
Рассмотрим процесс производства, в котором ресурсы преобразуются в определенный результат производства. В потребляемых ресурсах выделим 2 основных фактора производства: труд и капитал. Предположим, что факторы производства и его результат обладают однородностью, делимостью и поддаются количественному изменению х – труд, у – капитал. Результат производства зависит от его факторов. Z – результат. Зависимость Z= Z(х,у) – называется производством. Показатели эффективности использования факторов производства: показатель эффективности использования затрат труда называют производительностью труда, показатель эффективности использования капитала – фондом отдачи. Средняя производительность труда – это средняя величина результата, приходящаяся на каждую единицу затрат труда: Pa(x,y)=Z(x,y)/x .
Средняя фондоотдача – это средняя величина результата, приходящаяся на каждую единицу основных производственных фондов. Fa(x,y)=Z(x,y)/y.
Приростная производительность труда – это средняя величина дополнительного результата, приходящаяся на каждую дополнительную единицу дополнительно использованных единиц затрат труда. Fa(x,y)= ∆Z(x,y)/∆x=Z(x+∆x,y)-Z(x,y)/∆x
Приростная фондоотдача – это средняя величина дополнительного результата, приходящаяся на каждую дополнительно использованную единицу основных производственных фондов:
Fa(x,y)= ∆Z(x,y)/∆у=Z(x,у+∆y)-Z(x,y)/∆у
Предельная производительность труда – это предел приростной производительности труда при условии, что дополнительная величина затрат труда стремится к 0.
P(x,y)=lim P∆(x,y)= lim( ∆Z(x,y)-Z(x,y))/∆x
Предельная фондоотдача – это предел приростной фондоотдачи при условии, что величина дополнительно используемых основных производственных фондов стремится к 0.
f(x,y)=lim f∆(x,y)= lim( ∆Z(x,y)-Z(x,y))/∆y/
45. Производственная функция Кобба-Дугласа. Экономический смысл ее параметров, показатели эффективности и предельной эластичности по каждому фактору.
Производственная функция Кобба-Дугласа - зависимость объема производства (Q) от создающих его труда (L) и капитала (K). Общий вид функции:
![]()
Где А — технологический коэффициент, α — коэффициент эластичности по труду, а β — коэффициент эластичности по капиталу.
46. Понятие п-мерного вектора. Линейные операции над векторами. Свойства линейных операций.
.
Любой упорядоченный набор из п
действительных чисел a1,
a2,
..., ап
называется п-мерным
вектором
![]() ;
при этом числа, составляющие упомянутый
набор, называются координатами
(компонентами) вектора
.
;
при этом числа, составляющие упомянутый
набор, называются координатами
(компонентами) вектора
.
Определение 2. Совокупность всех n-мерных векторов называется n-мерным векторным пространством Rn.
Координаты n-мерного вектора можно расположить либо в строку:
![]()
либо в столбец:
![]()
Определение 3. Два вектора с одним и тем же числом координат
![]()
называются равными, если их соответствующие координаты равны, т.е.
![]()
Определение 4. Вектор, все координаты которого равны нулю, называется нулевым вектором
![]()
