
- •Элементы комбинаторики: перестановки, размещения сочетания. Примеры
- •Совместные и несовместные события. Теорема сложения вероятностей (док-во). Примеры.
- •4. Зависимые и независимые события. Теорема умножения вероятностей (док-во). Примеры.
- •Доказательство
- •5. Условная вероятность. Теорема о формуле полной вероятности, формулы Бейеса. Пример.
- •6. Понятие распределения вероятностей случайных событий. Схема независимых испытаний. Формула Бернулли. Повторные независимые испытания. Формула Бернулли с выводом.
- •Свойства математического ожидания:
- •12. Непрерывные случайные величины. Вычисление математического ожидания и дисперсии для равномерно и нормально распределенных случайных величин.
- •26. Статистические гипотезы, постановка задачи построения критерия проверки статистической гипотезы. Уровень значимости и мощность критерия.
- •Доверит. Интервал для a при известном параметре σ.
- •Доверит. Интервал для a при неизвестном параметре σ.
Доверит. Интервал для a при известном параметре σ.
Пусть x1, x2,…,xn — выборка из N(a, σ), причем a неизвестно, а σ известно.
Построить доверительный интервал для a при заданной доверительной вероятности (1- a).
Для решения задачи воспользуемся следующим фактом.
Пусть
X1,
X2,
Xn,
— независимые случайные величины,
распределение которых нормально с
параметрами a
и σ.
Тогда
случайная величина
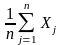 нормальна
с параметрами a
и
нормальна
с параметрами a
и
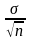 .
Для
обоснования этого утверждения достаточно
вычислить плотность распределения
.
.
Для
обоснования этого утверждения достаточно
вычислить плотность распределения
.
Статистика
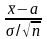 имеет нормальное распределение с
параметрами (0,1)(стандартное нормальное
распределение). Пусть
имеет нормальное распределение с
параметрами (0,1)(стандартное нормальное
распределение). Пусть
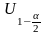 —
квантиль
порядка
—
квантиль
порядка
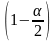 стандартного нормального распределения.
Тогда
стандартного нормального распределения.
Тогда
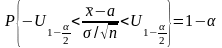 ,
следовательно
,
следовательно
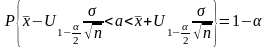 .
Таким образом статистики
.
Таким образом статистики
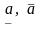 задаются
равенствами
задаются
равенствами
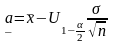 ,
,
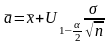 ,
и доверит. интервал для a
построен.
,
и доверит. интервал для a
построен.
Доверит. Интервал для a при неизвестном параметре σ.
Пусть x1, x2,…,xn — выборка из N(a, σ), причем a и σ неизвестны.
Построить доверительный интервал для a при заданной доверительной вероятности (1- a).
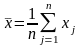 ,
,
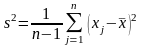
Для
решения воспользуемся теоремой:
Пусть x1,
x2,…,xn
— выборка из N(a,
σ),
Статистика
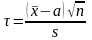 имеет
распределение Стьюдента с (n
- 1)
степенью свободы. (Без доказательства)
имеет
распределение Стьюдента с (n
- 1)
степенью свободы. (Без доказательства)
Построим,
пользуясь этой теоремой, доверительный
интервал для a.
Для этого прежде всего заметим, что
плотность вероятности распределения
Стьюдента с (n
- 1)
степенью свободы является четной и
положительной функцией x.
Поэтому,
если
—
квантиль
распределения Стьюдента с (n
- 1)
степенью свободы порядка
(то есть корень уравнения F(U)
=
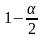 ,
где F(U)
— функция распределения Стьюдента с
(n
- 1)
степенью свободы), то
,
где F(U)
— функция распределения Стьюдента с
(n
- 1)
степенью свободы), то
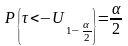 ,
следовательно,
,
следовательно,
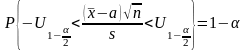 ,
,
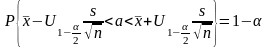 .
.
Итак,
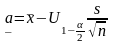 ,
,
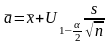 ,
и задача решена
,
и задача решена
