Вопрос 8 Непрерывные случайные величины. Функция плотности вероятности и ее свойства.

Определение. Случайная величина Х называется непрерывной, если ее функция распределения непрерывна в любой точке и дифференцируема всюду, кроме, быть может, отдельных точек.

На рисунке показана функция распределения непрерывной случайной величины Х, дифференцируемая во всех точках, кроме трех точек излома.

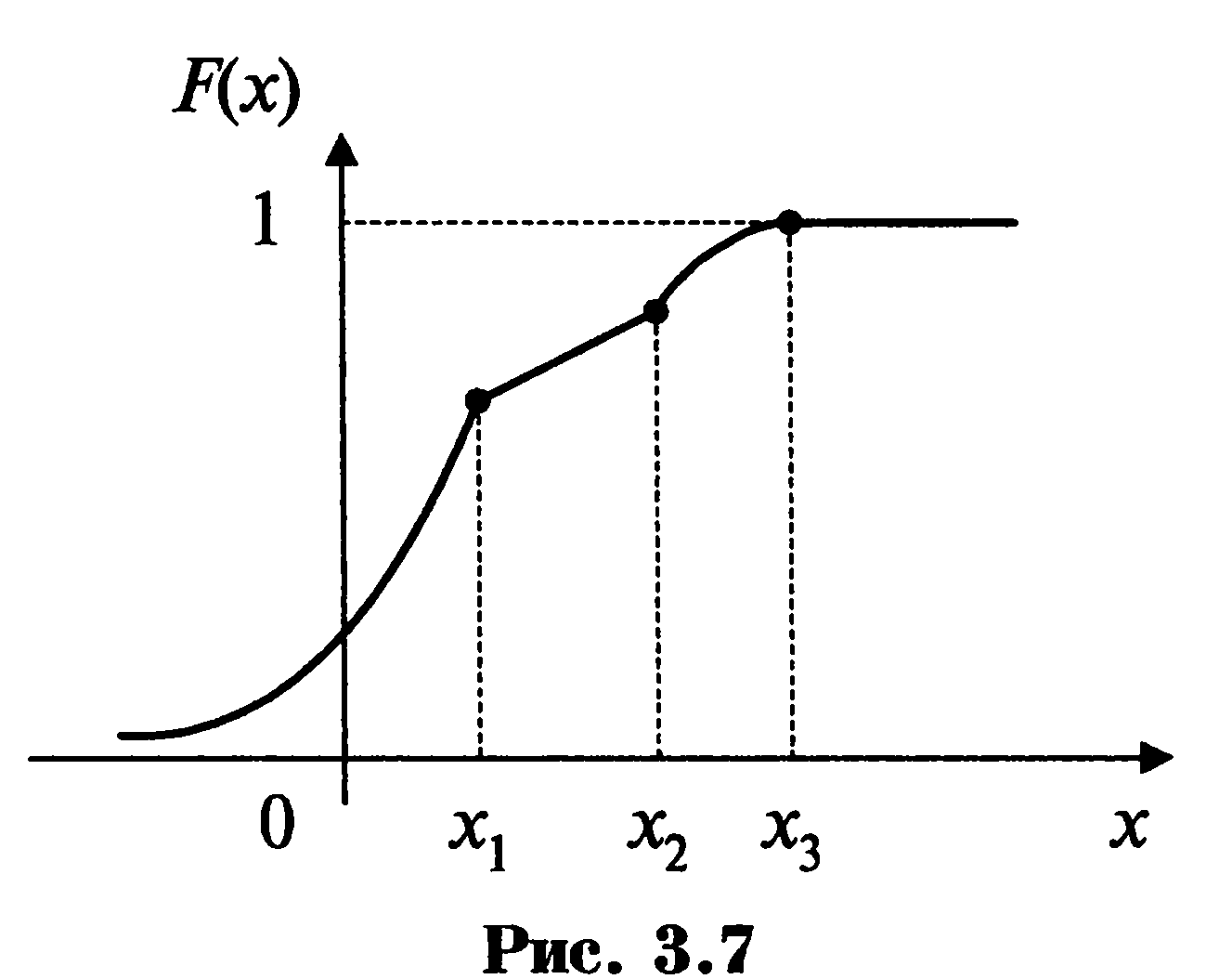
Т еорема. Вероятность любого отдельно взятого значения непрерывной случайной величины равна нулю. ( Поэтому непрерывную случайную величину можно было определить и иначе: случайная величина непрерывна, если вероятность любого отдельно взятого ее значения равна 0)

Доказательство: Покажем, что для любого значения x₁ случайной величины Х вероятность Р(Х=х₁)=0. Представим Р(Х=х₁) в виде

применяя свойство функции распределения случайной величины Х ( свойство: вероятность попадания случайной величины в интервал [x1, x2) (включая х1) равна приращению ее функции распределения на этом интервале, т. е. ) и учитывая непрерывность F(x), получим Т. доказана

Следствие. Если X — непрерывная случайная величина, то

вероятность попадания случайной величины в интервал (xi,X2) не

зависит от того, является этот интервал открытым или закрытым,

т.е.

Определение. Плотностью вероятности (плотностью

распределения или просто плотностью) (x) непрерывной

случайной величины X называется производная ее функции распределения.

Про случайную величину X говорят, что она имеет

распределение (распределена) с плотностью на определенном

участке оси абсцисс.

Плотность вероятности , как и функция распределения

F(x), является одной из форм закона распределения, но в

отличие от функции распределения она существует только для

непрерывных случайных величин.

Плотность вероятности иногда называют дифференциальной

функцией или дифференциальным законом распределения.

График плотности вероятности называется кривой

распределения.

Свойства плотности вероятности

непрерывной случайной величины.

1. Плотность вероятности—неотрицательная функция, т.е.

0.

Док-во: как производная монотонно неубывающей

функции F(x).

2. Вероятность попадания непрерывной случайной величины в

интервал [а,b] равна определенному интегралу от ее плотности

вероятности в пределах от а до b, т.е.

Р{а ≤ X ≤b) =

Док-во: Согласно свойству функции распределения

Р(а X ) = F(b) - F(a).

Так как F(x) есть первообразная для плотности вероятности

(ибо F’(x) = ), то по формуле Ньютона—Лейбница

приращение первообразной на отрезке [а, b] есть определенный

интеграл , т.е. формула верна.

Геометрически полученная вероятность равна площади

фигуры, ограниченной сверху кривой распределения и

опирающейся на отрезок [a,b]

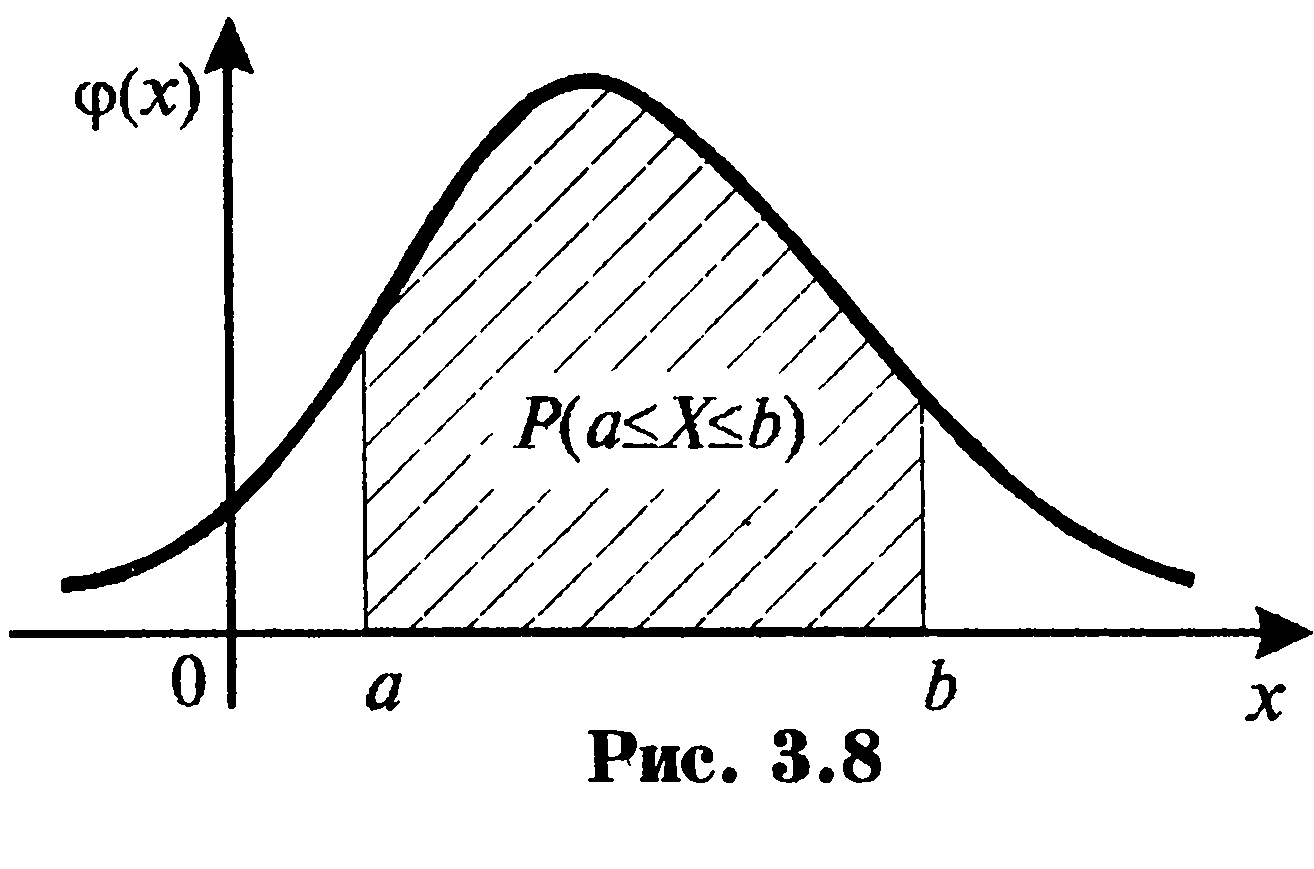
3. Функция распределения непрерывной случайной величины

может быть выражена через плотность вероятности по формуле:

Док-во: Формула получается из свойства 2 при если верхний предел b заменить на переменный предел х.

Геометрически функция распределения равна площади

фигуры, ограниченной сверху кривой распределения и лежащей

левее точки х .

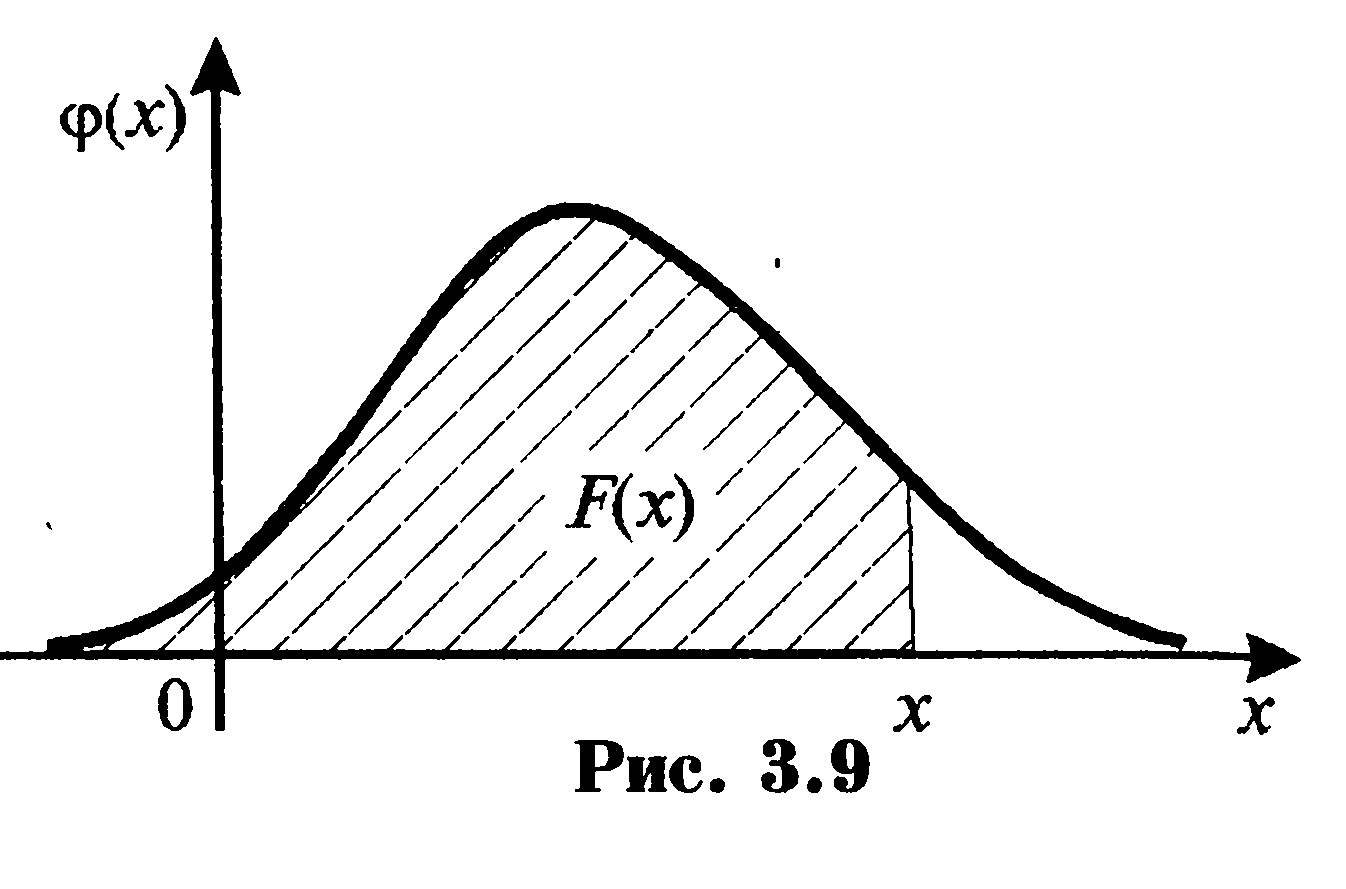
4. Несобственный интеграл в бесконечных пределах от

плотности вероятности непрерывной случайной величины равен единице:

По формуле т. е. свойство верно.

Геометрически свойства 1 и 4 плотности вероятности

означают, что ее график — кривая распределения — лежит не ниже

оси абсцисс, и полная площадь фигуры, ограниченной кривой

распределения и осью абсцисс, равна единице.