Вопрос 4. Условная вероятность . Зависимые и независимые события. Теорема умножения. Совместные и несовместные события. Теорема сложения.

•Пусть событие А и В рассматриваются в некотором опыте. Наступление одного (А) может влиять на наступление другого (В). Для характер-ки зависимости 1-ого события на 2-ое и вводится понятие условной вер-ти.

Опред. Условной вер-ю соб. В при условии , что соб.А произошло, наз-ся отношение вероятности произведения этих событий к вер-ти соб.А , причём обязательно вер-ть. соб. А должна быть не равно нулю.

Р(В/А)= , (1) где Р(А) не равно нулю

Вероятность с.В в отличие от условной тогда наз. безусловной.

Условн. вер-ть удовл-ет аксиомам:

1. Р(В/А)=

2. Р(

3. Р((В+С)/А)=Р(В/А)+Р(С/А)

•Из формулы (1) вытекает след. соотношение Р(А*В)=Р(А)*Р(В/А)=Р(В)*Р(А/В) (2)

Ф.(2) называют теоремой или правилом умножения

Опред. Соб.А наз-ем не зависимым от соб.В, если его условная вер. равно безусловной, а именно Р(А/В)=Р(А) (3)

Лемма о взаимной независимости событий. Если соб.А не зависит от В то и В не зависит от А. Док-во: из ф.(2) с учетом (3) следует в независимости от А

Опред.(др. опред. независимости событий) Соб. А1, А2,…,Аn наз. независим. (в совокупности) если каждое соб. Аi не завис. от произвед. любого числа остальных соб. и от каждого в отдельности, в противном случае соб. А1,А2,…,Аn наз. завис-ми.

Если с.А и В , где А*В , то справ-во Р(А+В) = Р(А)+Р(В) только для несовместных соб.

• Теорема сложения. P(A)+P(B)-P(A*B)

Док-во: представим соб. А+В и с.В в виде суммы 2-ух несовмест. соб. А+В=А+В*

В=А*В+В* Р(А+В)=Р(А) + Р(В) – Р(А*В)

Для того чтобы найти вероятность суммы нескольких совместимых событий проще использовать рав-во Р(S)*Р( , где

Вывод: P(S)=1-P( ) или P(A1+A2+An)=1-P

Опред. Два события на-ся несовместными, если наступление одного исключает наступление другого. Иначе событие наз. совместными. Набор событий А1,А2,..Аn называют попарно несовместными, если любые два из них несовместны.

А1,А2,…Аn образуют полную группу если выполняют два условия:

1. Попарно несовместны (Аi*Aj 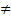0)

2. В условиях опыта происходят одно и только одно из них (Ai+…*An=Ω)

Несколько событий в условиях опыта назовём равновозможными, если ни одно из них не является объективно более возможным чем другие.

Вопрос 6.Схема Бернулли. Формула бернулли, свойства вероятностей бернулли

Если вероятность наступления события А в каждом испыта­нии не меняется в зависимости от исходов других, то такие ис­пытания называются независимыми относительно события А. Если независимые повторные испытания проводятся при одном и том же комплексе условий, то вероятность наступления события А в каждом испытании одна и та же. Описанная последовательность независимых испытаний получила название схемы Бернулли.

Схема Бернулли- вероятностная схема повторений независимых испытаний.

Определение: Последовательность n-независимых испытаний, в каждой из которых может произойти некоторое событие А (его называют “успехом”) c вероятностью P(A)=p или не произойти с вероятностью P( )=1-P(A)=1-p=q ; ( называют “неуспехом”), называется схемой Бернулли.

Например: При стрельбе по мишени А-“успех”, - “промах”.

В любой такой схеме пространство элементарных событий состоит из 2-х элементов, т. е. Ω= ; -успех, -не успех; A= ; = ; P(A)=p; P( )=q=1-p

Для n=3(опыт повторяется 3 раза)

Ω= ; Ω= ; Ω= ; Ω= ; Ω= ; Ω= ; Ω= ; Ω=

Вероятность каждого определяется однозначно по т. умножения P( )= =qqp= ;

Если , , то каждый элемент исходящий из n испытаний будет соответствовать последовательность из 0 и 1.

Свойства Вероятностей Бернулли

1). F(x) огранич. ,0 ≤F(x) ≤1

2). F(x) неубывающая каждая x принадлежит R, т. е. если следовательно F( ) ≤F( )

3). F(- )=0 ; F(+ )=1

4). P =F(b)-F(a)

5). F(x) непрерывна слева, т. е.

Формула Бернулли

Теорема: Если производится n независимых испытаний в каждом из которых вероятность события Аp и события A(1-p), то вероятность что события А произойдет ровно m раз, определяется формулой Бернулли: ; m=0,1,2,…,n

Док-во: Рассмотрим вероятность сложных событий, состоящих в том, что интереснастоящего события А произойдет в 1х испытаниях, а не произойдет в n-m испытаниях.

ААА…

mp n-mp

по теореме умножения:

Вероятность другого сложного события, в котором событие А наблюдается m раз, но в другом порядке, будет той же

Число таких сложных событий, в которых событие А появляется m раз равно числу сочетаний , так как все эти сложные события несовместны, то по теореме сложения искомая вероятность сумме вероятности всех таких сложных событий, т. е. можно заметить, что в вероятность является коэффициентом в разложении генома +pⁿxⁿ

–биноминальный закон распределения.

(x)= - производящая функция для последовательности независимых испытаний.

Если в каждом отдельном испытании вероятности наступления события А разные, то вероятность, что событие А наступит m раз равно коэффициенту при степени m многочлена .

)( )+…( )- производящая функция для последовательности испытаний с разными вероятностями успеха.

Если в n независимых, в каждом из которых может происходить событие с соответствующими вероятностями , то вероятность того, что в n опытах событие равна: где (палиоминальное распределение вероятности). 0≤m≤n