24) Непараметрические критерии. Критерий согласия Пирсона.
Статистические гипотезы делятся на
- о значениях параметров известного распределения генеральной совокупности ГС (параметрические); параметрический критерий ( их распределение должно быть известно)
- о виде неизвестного распределения ГС (непараметрический критерий, критерий согласия)
Постановка задачи:
Дано: выборочные данные ( x1,….xn), любое xi - случайная величина (СВ) с неизвестной функцией распределения.
Утверждение: xi имеют
некоторое известное распределение
(
).
Проверить, что распределение xi именно то, которое указано в утверждении.
:
xi имеют другое распределение.
Обычно, параметры распределения из не известны. Поэтому их приходится оценивать по выборочным данным. Если обозначить r – количество оцениваемых по выборочным данным параметрам, то при r=0 - все параметры известны (критерий Колмогорова). При r>0 – имеются неизвестные параметры. (критерий согласия)
Определение: Критериями согласия называются статистические критерии для проверки гипотезы о предполагаемом виде неизвестного распределения. Он используется для проверки согласования предполагаемого вида распределения с выборочными данными.
Существуют различные критерии согласия:
- Пирсона
- Фишера
- Колмогорова
- Смирнова
Общая идея при выборе критерия согласия:
использовать в качестве меры расхождения
наблюдаемой плотности вероятности и
гипотетической плотности вероятности
некоторую статистику, имеющую распределение
(Пирсона).
По теореме Фишера такой статистикой
служит )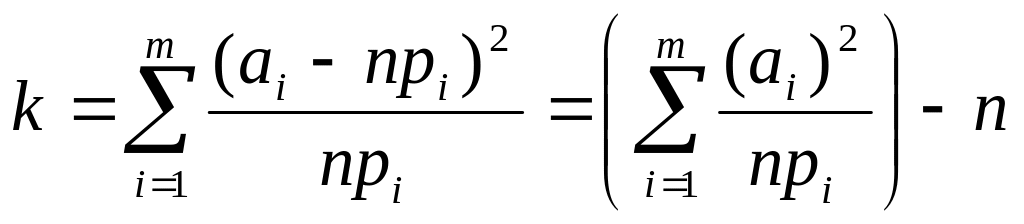
(1)
m - количество не пересекаемых интервалов, содержащие выборочные значения
ai – число наблюдаемых выборочных значений, попавших в интервал с номером i
– наблюдаемые частоты
pi – вероятности того, что
СВ с гипотетическим распределением
(
(попадет) примет значения в интервале
с i.
n*pi - математическое ожидание числа наблюдений, попавших в интервал с i (гипотетическая частота).
n= a1+…..+am
Теорема Фишера Если проверочная гипотеза о виде неизвестного распределения верна, то при большом объеме выборки n, критерий (1) имеет приблизительное - распределения с числом степеней свободы m-r-1, где m - количество интервалов разбиения, r – количество оценивания по выборочным параметрам.
Замечание 1. Чем ближе к 0 значения
критерия 1, тем правдоподобней выдвигаемая
гипотеза. Поэтому критическая область
данного критерия выглядит (k”,+∞),
k”= 
а
область принятия гипотезы для уровня
значимости α[0; 
]
Необходимое условие применимости критерия Пирсона (в реальных заданиях) является требование, чтобы в каждом интервале разбиения попадало не менее 5 выборочных значений.
Замечание 2. Если существуют
неизвестные параметры гипотетического
распределения, то вероятности 
неизвестно
тоже, поэтому неизвестный параметр θ
оценивается по выборке 
и затем оценим неизвестные вероятности
, 
принадлежит i-му интервалу,
где 
функция
предполагаемого распределения ( из
)
, тогда
{n
– оценка для гипотетических частот
k = 
(2)
Правила применения 
критерий
(1) или (2)
Вся область возможных значений СВ X разбиваем на интервалы Δ1, Δ2,….., Δm – не пересекаемые интервалы (либо равной, либо нет длины).
По формулам 2 вычисляют К наблюдаемое значение критерия.
По заданному уровню значимости α находят критическую точку К” =
К набл. ≤ К”
не противоречит опытным данным. К
набл. >К”
- отвергаем.
Замечание. Если
:
выборка из нормального распределения
N(a;
),
то длину интервальной группировки
выбирают h
0,4S;
или требуют, чтобы гипотетические
частоты n*
для
любой интервальной группировки должно
быть достаточно большим (n*
