22. Закон убывающей отдачи. Стадии деятельности фирмы в краткосрочном периоде.

Закон убывающей отдачи (law of diminishing returns), или закон убывающего предельного продукта, или закон изменяющихся пропорций, — все это различные названия одного закона. Рассмотрим два определения, под разным углом зрения объясняющие закон убывающей отдачи.

Закон убывающей отдачи гласит: по мере того как возрастает использование какого-либо производственного фактора (при фиксированных остальных производственных факторах) в итоге достигается точка, в которой дополнительное использование этого фактора ведет к снижению объема выпуска продукции.

Закон убывающей отдачи состоит в том, что, начиная с определенного момента, последовательное присоединение единиц переменного ресурса (например, труда) к неизменному, фиксированному ресурсу (например, капиталу или земле) дает уменьшающийся добавочный, или предельный, продукт в расчете на каждую последующую единицу переменного ресурса. Уточним перевод слова «предельный» — marginal. Marginal — близким к пределу, находящийся на краю. Для российского экономиста наиболее точный смысл выражают слова «добавочный», «дополнительный».

Иначе говоря, если численность сотрудников, обслуживающих данное направление деятельности, будет увеличиваться, то рост объема производства будет происходить после некоторого момента все медленнее, по мере увеличения числа рабочих на производстве.

Стадии деятельности фирмы в краткосрочном периоде:

Стадия 1 - стадия возрастающего предельного продукта. На этой стадии наблюдается непропорциональное соотношение труда и капитала: капитал (постоянный фактор производства) находится в избытке, а труда (переменный фактор производства) недостаточно, чтобы полностью загрузить производственные мощности. Наблюдается растущая отдача в производительности при увеличении пропорции между трудом и капиталом.

Стадия 2 - стадия убывающего предельного продукта - начинается с того момента, когда предельный продукт имеет максимальное значение, и продолжается до того, как предельный продукт труда станет равен нулю. Здесь соотношение труда и капитала, т.е. переменного и постоянного ресурсов, наиболее оптимальное. Только на данной стадии находится точка наиболее эффективного производства.

Стадия 3 - стадия отрицательного предельного продукта. На данной стадии количество труда - переменного фактора - слишком велико по отношению к капиталу - постоянному фактору производства.

В заключении следует отметить, что действие закона убывающего предельного продукта носит относительный характер, т.е. инновационное развитие раздвигает его границы. Совершенствование технологии ведет к тому, что некоторый объем производства может быть обеспечен при сокращении количества используемого переменного ресурса. Поэтому данный закон применим только на краткосрочном отрезке времени, когда хотя бы один из факторов производства носит постоянный характер.

22. Производственная функция и равновесие производителя в долгосрочном периоде. Развитие производства и отдача от масштаба.

Вводимые в производство ресурсы называются факторами производства. к важнейшим из них в современном обществе относятся земля, труд, капитал, предпринимательская способность и информация.

Технология – это определенный способ соединения (комбинация) факторов производства в едином производственном процессе, который определяет результирующий уровень выпуска при эффективном использовании факторов производства. Природа налагает на фирмы технологические ограничения: лишь некоторые комбинации ресурсов представляют собой практически осуществимые способы производства данного объема выпуска. Множество всех комбинаций вводимых ресурсов и выпусков, которые охватывают технологически достижимый способ производства, называется производственным множеством.

Предположим, что у нас имеется только один фактор производства, тогда производственное множество будет иметь следующий вид.

С войства производственного множества:

1) не пустое, 2) замкнутое множество (включает в себя и границу), 3) если затраты факторов равны 0, то и выпуск тоже: if x=0,то y=0. 4) возможность бездействия, выпуска еще нет, а мы несем невозвратные трансакционные издержки, 5) монотонность технологии: увеличение затрат по крайней мере одного фактора не ведет к уменьшению объема выпуска ¶y\¶xi ³0.

Производственная функция – наиболее удобный способ описания технологически эффективных способов производства. Производственная функция – граница производственного множества, следовательно она является максимально возможным уровнем производства при данном количестве факторов производства и данной технологии.

В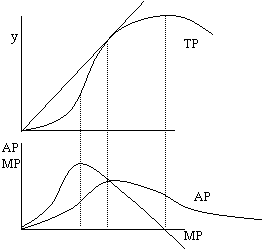 коротком периоде количество хотя бы одного ресурса остается постоянным. Посмотрим производственную функцию от переменного ресурса. f(x) – общий выпуск. Тогда Средний продукт данного ресурса . Предельным продуктом переменного фактора называют приращение общего продукта в связи с увеличением применения данного ресурса на единицу. .

Графически величина предельного продукта определяется тангенсом угла наклона касательной к кривой общего продукта в точке, соответствующей определенному его объему, величина АР – тангенсом угла наклона луча, идущего из начала координат к этой же точке. Кривая МС пересекает кривую АС в точке максимума последней. Докажем это: АР=у\х. Найдем . Условие первого порядка: 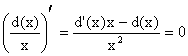Þ Þ МР=АРмах.

Снижение предельного продукта переменного ресурса получило название закона убывающей производительности.

Эластичность выпуска по факторам производства.

ei – эластичность выпуска по i-тому фактору производства равна отношению предельной производительности MPi i-того фактора к средней производительности.

; .

Þ Эластичность показывает (приблизительно) на сколько процентов увеличиться выпуск при увеличении затрат i-того фактора на 1% и при неизменных затратах других факторов.

.

Пример: y(K, L)=AKaLb; ; .

Изокванты и их свойства. В теории производства традиционно используется двухфакторная производственная функция (например, Q= f(L, K)). Изокванта – кривая, представляющая собой бесконечное множество комбинаций факторов производства (ресурсов), обеспечивающих одинаковый выпуск продукции. f(x1, x2)=y0, y0=const.

Свойства:

1.  (В отличие от кривых безразличия) мы точно знаем уровень производства, соответствующий данной изокванте.

2.  И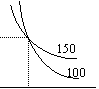 зокванты не пересекаются. Если бы они пересекались, то получилось бы, что одной и той же комбинации факторов соответствовали бы два разных уровня выпуска. Но изокванта показывает максимальный выпуск продукции, достигаемый при использовании определенных сочетаний ресурсов.

3.  Функция y=f(x1, x2) монотонно возрастает Þ изокванта, лежащая выше и правее другой, представляет собой больший объем выпускаемой продукции.

4.  Изокванты имеют отрицательный наклон.

5.  Изокванты выпуклы относительно начала координат.

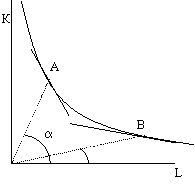
Предельная норма технологического замещения.

Наклон изоквант характеризует MRTS (marginal rate of technical substitution) одного ресурса другим. MRTS измеряет пропорцию, в которой фирме придется заменить один фактор другим, чтобы оставить выпуск без изменений.

или для непрерывного случая .

Рассмотрим изменение используемых факторов:

.

Вдоль изокванты dy=0, поэтому .

По мере увеличения количества фактора 1 и соответствующего изменения количества фактора 2, чтобы остаться на той же самой изокванте, технологическая норма замещения убывает. Убывание MRTS означает, что наклон изокванты должен убывать по абсолютной величине по мере движения вдоль изокванты в направлении увеличения х1 и наоборот.

Предельная норма технического замещения имеет тот недостаток, что она зависит от единиц, в которых измеряются объемы применяемых ресурсов. Этого недостатка нет у показателя эластичности замещения.

Эластичность замещения факторов производства.

Кривизна изокванты характеризует возможность (легкость) взаимного замещения факторов производства при сохранении одного и того же количества выпускаемой продукции.

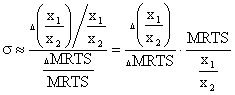
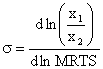, где MRTS³0.

s показывает, на сколько измениться соотношение факторов производства при изменении MRTS на 1% при сохранении объема производства. Т. к. вдоль изокванты х1\х2 и MRTS изменяются в одном направлении величина s всегда положительна.

M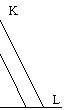 RTS меняется вдоль изокванты. Чем сильнее меняется наклон изокванты (MRTS) из одной точки в другую, тем сложнее заменить один фактор другим.

Тангенс угла луча, проведенного из начала координат до точки на изокванте показывает интенсивность применения различных ресурсов в определенном производственном процессе K\L. Þ Верхняя часть изокванты включает капиталоинтенсивные, тогда как нижняя – трудоинтенсивные производственные методы.

Линейная производственная функция. Линейная функция: y= f(K, L)=aK+bL.

Все изокванты такой функции представляют собой параллейные прямые линии с наклоном –b\a. Т. к. MRTS совсем не меняется при изменении отношения К\L, то эластичность замещения равна бесконечности.

Таким образом, линейная изокванта предполагает собой совершенную замещаемость производственных ресурсов.

Ф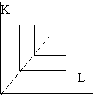 ункция Леонтьева (названа его именем, т. к. он положил такой тип изокванты в основу разработанного им метода затраты - выпуск).

Y=min (aK, bL) a, b >0.

Фирма с такой производственной функцией будет вседа функционировать на луче, где отношение факторов равно b\a. Находиться в другой точке на изокванте неэффективно, т. к. тот же объем можно произвести, используя меньшее количество факторов. Поэтому в случае жесткой дополняемости ресурсов, когда труд и капитал комбинируются в единственно возможном соотношении, MRTS равна 0, эластичность замещения факторов равна 0.

Ф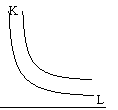 ункция Кобба-Дугласа. Производственная функция, у которой эластичность замещения факторов равна единице, называется функцией Кобба-Дугласа. Ее изокванты имеют классическую, выпуклую форму.

Y=f(K, L)=AKaL1-а, A, a=сonst >0.

.

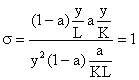Эффект отдачи от масштаба. Если выбран технически эффективный способ производства, то увеличение выпуска возможно за счет пропорционального увеличения использования всех производственных ресурсов. Это и есть изменение масштаба производства.

Пусть первоначальное соотношение между выпуском и применяемыми ресурсами описывается производственной функцией Q0=f(K, L). Если мы увеличим объемы применяемых ресурсов в k раз, то новый объем выпуска составит Q1=f(kK, kL). Если в результате выпуск увеличиться также в k раз (Q1=kQ0), то наблюдается постоянная отдача от масштаба. Если выпуск увеличиться менее чем в k раз (Q1<kQ0), то имеет место убывающая отдача от масштаба. И соответственно если Q1<kQ0, то отдача от масштаба возрастающая.

Разумеется, одна и та же технология может характеризоваться различной отдачей от масштаба при разных уровнях производства. Вполне может случиться, что при более низких объемах производства технология характеризуется возрастающей отдачей от масштаба, позднее, при более высоких уровнях – постоянной и убывающей.

Введем еще одну характеристику производственной функции – однородность. Производственная функция называется однородной, если при увеличении количества всех производственных ресурсов в k раз выпуск увеличивается в kt раз, так что

Q1(kK, kL)= kt Q0(K, L).

Показатель t характеризует степень однородности функции.

Если t=1, тол отдача от масштаба постоянна, а производственная функция в этом случае обычно называется линейно-однородной.

Если t<1, имеет место убывающая отдача от масштаба.

Если t>1 – возрастающая отдача.

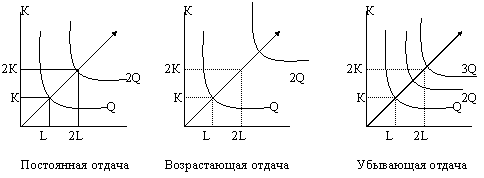
Для однородной производственной функции отдача от масштаба может быть представлена графически. Показателем отдачи может случить расстояние вдоль луча, проведенного из начала координат, между изоквантами, представляющими кратные Q объемы выпуска – Q, 2Q, 3Q и т. д.

Постоянная отдача от масштаба наблюдается в тех производствах, где ресурсы однородны (в техническом смысле) и их количество можно менять пропорционально. Фирма может просто повторить то, что она делала раньше, путем кратного увеличения всех факторов. Убывающая отдача, как правило, связана с ограниченными возможностями управления крупным производством.

2 вариант ответа

Производственная функция определяет максимальный объём выпуска продукции при

каждом заданном количестве ресурсов. Она имеет вид: Q=f(x1,x2…xn) x1, x2 … xn – это

ресурсы используемые в данном производстве.

Изокванта – это график изображения двухфакторной производственной функции. Она

показывает комбинации двух переменных факторов, обеспечивающих один и тот же

выпуск продукции.

Взаимосвязь между изменением масштаба производства и соответствующем изменением

V выпуска продукции – называется отдачей от масштаба. Отдача бывает растущей,

снижающейся и постоянной. При растущей каждая следующая единица продукции

требует всё меньшее количество обоих факторов при неизменном их соотношении. При

снижающей отдаче на каждую следующую единицу продукции приходится затрачивать

всё большее количество факторов производства при неизмененном их соотношении. В

случае постоянной отдаче от масштаба одинакового приращения выпуска будет при

пропорциональном изменение факторов производства.