1.2. Вычисление пределов

Рассмотрим . Если подставить в выражение значение х=3, то получим неопределенность вида . Чтобы вычислить данный предел, надо преобразовать тождественным образом выражение, стоящее под знаком предела:

при .

Выражение х+3 совпадает с исходным при всех значениях х, кроме х=3, и не содержит неопределенность. Тогда, поскольку функция, стоящая под знаком предела, может быть не определена в самой предельной точке, справедливо равенство .

Пример 1. Вычислить при значениях: х₀ = 1, х₀ = -4, х₀ = 4, а также при .

Функция определена при всех значениях х кроме х=4 и х= -4. Тогда при , согласно (2) получим:

.

При знаменатель является величиной б.м., а числитель конечной, тогда, согласно свойствам (3), имеем .

При и числитель, и знаменатель обращаются в нуль, т.е. имеет место неопределенность вида . Выполним преобразования, тождественные при , т.е. выделим в числителе и знаменателе сомножитель (х+4) и сократим на него дробь. Полученное выражение не будет содержать неопределенность:

.

При и числитель и знаменатель являются б.б. величинами, т.е. имеет место неопределенность . Разделим слагаемые числителя и знаменателя на х² (2-старшая степень среди степеней всех слагаемых числителя и знаменателя), а затем воспользуемся свойствами (1) и (3):

.

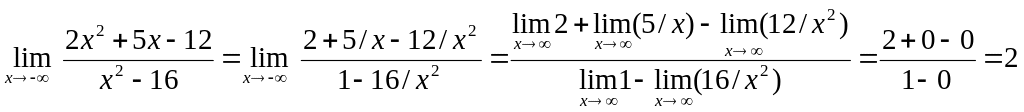Указанный способ устранения неопределенности вида при основан на том, что , где С – постоянная, а > 0.

Аналогично вычисляются пределы:

;

.

Выше были рассмотрены простейшие примеры вычисления пределов. В более сложных случаях следует применять другие приёмы раскрытия неопределенностей, в частности, использовать, так называемые, замечательные пределы:

;

; ,

Где е =2,718281828459045…. а

Пример 2. Вычислить .

Преобразуем выражение, стоящее под знаком предела таким образом, чтобы можно было применить замечательные пределы 1 и 3:

Введём новые переменные : при ; , тогда последнее выражение можно переписать:

.

2. Начало дифференциального и интегрального исчисления.

2.1. Производная и дифференциал.

Напомним определение основного понятия дифференциального исчисления – производной.

Пусть х₀ фиксированное значение аргумента функции f(x), определенной на промежутке Х. Придадим значению х₀, отличное от нуля приращение ∆х такое, что х₀+∆х тоже принадлежит Х. Отметим, что приращение ∆х может быть любого знака. Приращению ∆х соответствует приращение функции ∆f(х₀)=f(х₀+∆х) - f(х₀). Тогда, если существует конечный предел отношения приращения ∆f(х₀) функции f(x) к приращению аргумента ∆х при стремлении ∆х к нулю, то он называется производной функции f(x) в точке х₀ и обозначается f′(х₀):

. (4)

Полученная по формуле (4) производная f′(х₀) – число. Если предел в (4) равен бесконечности, то говорят, что функция f(x) имеет в точке х₀ бесконечную производную. Возможен также случай, когда предел (4) не существует.

Из курса физики известно, что если за время ∆t = t - t₀ пройдено расстояние ∆S, то средняя скорость за время равна , а предел является скоростью движения в момент t₀ , которую называют мгновенной скоростью .

Тогда для произвольной функции f(x) отношение - средняя скорость изменения функции f(x) при изменении аргумента на величину ∆х , а - есть мгновенная скорость изменения функции f(x) при значении аргумента х₀.

Например, если функция у=f(x) описывает зависимость полных издержек производства у от объема выпускаемой продукции х, то - себестоимость продукции при данном объеме производства х₀.

Если предел (4) существует для всех значений х из Х, то каждому х можно сопоставить значение предела и тем самым задать новую функцию, которую называют производной функции f(x) и обозначается . Возможны и другие обозначения производной, например, . Индекс х в указывает переменную, по которой вычисляется производная.

Поскольку является функцией, то от нее тоже можно взять производную , которая будет производной второго порядка или второй производной (или ) от исходной функции f(x). Аналогично , где и - производные n-го (n-1) –го порядка, соответственно.

Обратимся к геометрическому смыслу производной. Выберем на графике функции f(x) (Рис.6) две точки и , абсциссы которых отличаются на приращение ∆х, а ординаты, соответственно на Проведем секущую через точки М₀ и М и обозначим , отсчитанный против часовой стрелки угол, который секущая образует с положительным направлением оси абсцисс. При стремлении ∆х к нулю точка М, перемещаясь по графику функции, стремится к точке М₀, при этом секущая ММ₀, поворачивается вокруг точки М₀ и стремится занять предельное положение касательной, проведенной к графику функции через точку М₀. Обозначим угол, который касательная образует с положительным направлением оси абсцисс. Тогда из треугольника ∆М₀КМ имеем:

Рис.6

.

Следовательно, если производная функции f(x) в точке х₀ существует и конечна, то ее значение равно тангенсу угла наклона касательной, проведенной к графику функции в точке .

Как видно из рис.6, приращение функции , соответствующее приращению аргумента , равно приращению ординаты кривой

.

Из геометрического смысла производной и свойств треугольника ∆М₀КМ следует, что приращение ординаты касательной равно

.

Из рис.6 видно, что отрезок МК не равен отрезку NK, т.е. не равно . Можно показать, что если в точке х функция f(x) имеет конечную производную, то справедливо равенство

.

где - бесконечно малая величина при . Линейная по часть приращения называется дифференциалом функции и обозначается df, т.е. . Если то (см. ниже табл. производных), так что , т.е. дифференциал независимой переменной совпадает с ее приращением. Тогда для дифференциала df функции f(x) имеем

. (5)

Именно так обычно и записывается дифференциал первого порядка или просто дифференциал. Помимо дифференциалов первого порядка можно определить дифференциалы высших порядков:

.

Производная любой функции может быть вычислена по определению (4) . Однако, вычисления значительно упрощаются, если применять правила дифференцирования и таблицу производных, содержащую производные от элементарных функций. Эти производные можно получить по формуле (4).

Таблица производных

1)		8)
2)		9)
3)		10)
4)		11)
5)		12)
6)		13)
7)		14)