Барометрическая формула — определяет зависимость давления или плотности газа от высоты в поле тяжести

 

Давайте теперь узнаем, откуда же получается барометрическая формула. Давление газа на некой высоте, определяется как :

 

Теперь возьмем колонну в атмосфере и выделим в ней тонкий слой воздуха высотой dh. Ясно, что такой слой вызывает изменение давления на величину dP :

 

Знак минус необходим для того, что с увеличением высоты давление уменьшается

Рассматривая атмосферный воздух как идеальный газ, можно воспользоваться уравнением Менделеева — Клапейрона

 

Из этого уравнения выражаем давление

 

А теперь можно и плотность газа

 

Подставляя найденную плотность газа в дифференциальное уравнение dP, мы получаем :

 

Сделав все преобразования. мы получаем зависимость давления P от высоты подъема h. Теперь необходимо проинтегрировать обе части нашего уравнения:

 

Проинтегрировав, у нас полечилась вот такое уравнение:

 

И теперь последний рывок, это взять логарифм. И у нас получится Барометрическое уравнение.

 

В Формуле мы использовали :

— Давление газа (атмосферное)

— Давление газа над уровнем моря

— Высота над уровнем моря

— Плотность газа

— Ускорение свободного падения

— Постоянная Больцмана

— Температура

— Масса одной молекулы

— Универсальная газовая постоянная

— Молярная масса

— Количество вещества

— Число Авогадро

Концентрация молекул n - число молекул в единице объема. Другие формулы, где встречается концентрация молекул: Число молекул N 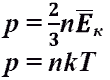Давление газа p

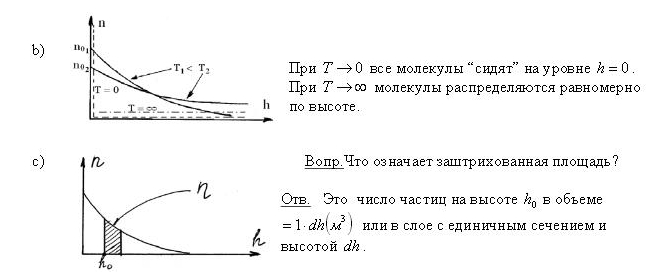
В присутствии гравитационного поля (или, в общем случае, любого потенциального поля) на молекулы газа действует сила тяжести. В результате, концентрация молекул газа оказывается зависящей от высоты в соответствии с законом распределения Больцмана:

n = n₀exp( -mgh / kT )

где n - концентрация молекул на высоте h, n₀ - концентрация молекул на начальном уровне h = 0, m - масса частиц, g - ускорение свободного падения, k - постоянная Больцмана, T - температура.

Если высота сосуда много меньше чем kT/mg, то зависимостью концентрации от высоты можно пренебречь. С другой стороны, в атмосфере концентрация молекул быстро уменьшается с увеличением высоты и, поэтому, величина атмосферного давления также уменьшается. Принимая во внимание, что P = nkT, мы можем записать так называемую барометрическую формулу, описывающую изменение атмосферного давления в зависимости от высоты:

P = P₀exp( -mgh / kT )

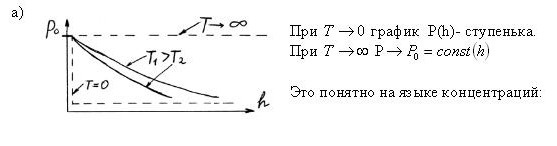
_12. Барометрическая формула как частный случай распределения Больцмана. Нормировка распределения Больцмана. Примеры использования функции распределения Больцмана.

Если атмосферное давление на высоте h равно р (рис. 1), то на высоте h+dh оно равно p+dp (при dh>0 dp<0, так как давление с высотой уменьшается). Разность давлений р и p+dp равна весу газа, заключенного в объеме цилиндра высотой dh с основанием площадью 1 м²: где ρ — плотность газа на высоте h (dh настолько мало, что при изменении высоты в этом интервале плотность газа можно считать постоянной). Значит, (1) Зная уравнение состояния идеального газа pV=(m/M) RT (m — масса газа, М — молярная масса газа), находим, что Подставив это выражение в (1), получим или С изменением высоты от h₁ до h₂ давление изменяется от р₁ до р₂ (рис. 67), т. е. или (2) Выражение (2) называется барометрической формулой. Она позволяет вычислить атмосферное давление в зависимости от высоты или, измеряя давление, найти высоту: Так как высоты считаются относительно уровня моря, где давление считается нормальным, то выражение (2) может быть представлено в виде (3) где р — давление на высоте h. Прибор для определения высоты над земной поверхностью называется высотомером (или альтиметром). Его работа основана на применении формулы (3). Из этой формулы следует, что чем тяжелее газ, тем давление с высотой убывает тем быстрее. Барометрическую формулу (3) можно преобразовать, если воспользоваться формулой p=nkT: где n – концентрация молекул на высоте h, n₀ – то же, на высоте h=0. Так как M=m₀N_A (N_A – постоянная Авогадро, m₀ – масса одной молекулы), a R=kN_A, то (4) где m₀gh=P — потенциальная энергия молекулы в поле тяготения, т. е. (5) Выражение (5) называется распределением Больцмана для внешнего потенциального поля. Из него видно, что при постоянной температуре плотность газа больше там, где меньше потенциальная энергия его молекул. Если частицы находятся в состоянии хаотического теплового движения и имеют одинаковую массу и , то распределение Больцмана (5) применимо в любом внешнем потенциальном поле, а не только в поле сил тяжести.

условие нормировки:

(N – полное число частиц в газе)

Уравнение Больцмана используется для изучения переноса тепла и электрического заряда в жидкостях и газах, и из него выводятся транспортные свойства, такие как электропроводность, эффект Холла, вязкость и теплопроводность. Уравнение применимо для разреженных систем, где время взаимодействия между частицами мало (гипотеза молекулярного хаоса).

_13. Процессы переноса: диффузия, теплопроводность, вязкость. Формулы для вязкости и теплопроводности идеального газа. Формула для коэффициента диффузии идеального газа.

Диффу́зия (лат. diffusio — распространение, растекание, рассеивание, взаимодействие) — процесс взаимного проникновения молекул или атомов одного вещества между молекулами или атомами другого, приводящий к самопроизвольному выравниванию их концентраций по всему занимаемому объёму.

Теплопрово́дность — это процесс переноса внутренней энергии от более нагретых частей тела (или тел) к менее нагретым частям (или телам), осуществляемый хаотически движущимися частицами тела (атомами, молекулами, электронами и т. п.). Такой теплообмен может происходить в любых телах с неоднородным распределением температур, но механизм переноса теплоты будет зависеть от агрегатного состояния вещества.

Вя́зкость (вну́треннее тре́ние) — одно из явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. В результате происходит рассеяние в виде тепла работы, затрачиваемой на это перемещение.

Для Вязкости идеальных газов в молекулярно-кинетической теории даётся следующее соотношение:   где m — масса молекулы, n — число молекул в единице объёма,  — средняя скорость молекул и l — длина свободного пробега молекулы между двумя соударениями её с другими молекулами.

Теплопроводность:

где r-плотность, С_V - теплоемкость при постоянном объеме, -ср. скорость движения частиц, -длина своб. пробега частиц. теплопроводность к. Т пропорциональна 1/р, а r~p (р- давление газа), теплопроводность идеального газа не зависит от р.

Коэффициент диффузии – количественная характеристика скорости диффузии, равная количеству вещества (в массовых единицах), проходящего в единицу времени через участок единичной площади (например, 1м²) при градиенте концентрации, равном единице (соответствующем изменению 1 моль/л → 0 моль/л на единицу длины)

_14. Процесс диффузии в идеальном газе. Формула для коэффициента диффузии идеального газа. Формулы для вязкости и теплопроводности идеального газа.

Предположим, что в единице объёма двухкомпонентной газовой смеси содержится n1 молекул одного вида и n2 молекул другого вида. Полное число молекул в единице объёма равно n = n1 + n2­. Допустим, что в направлении оси х создаются градиенты концентраций , причём . Тогда, , так что n, а, следовательно, и Р постоянны (в силу Р = nkT).

В этом случае газодинамических потоков не возникает. Однако вследствие теплового движения молекул будет происходить процесс выравнивания концентраций, сопровождающийся переносом массы каждой из компонент в направлении убывания её концентрации. Этот процесс носит название диффузии. Диффузия наблюдается так же в жидких и твёрдых телах.

Поток молекул i – го вида через перпендикулярную к оси х поверхность S определяется выражением

,

где D – коэффициент пропорциональности, называемый коэффициентом диффузии. Знак минус указывает на то, что поток молекул направлен в сторону убывания концентрации. Умножив обе части этого равенства на массу молекулы i – го вида mi, получим выражение для потока массы i – ой компоненты:

,

где i = nimi – парциальная плотность i – ой компоненты.

Для Вязкости идеальных газов в молекулярно-кинетической теории даётся следующее соотношение:   где m — масса молекулы, n — число молекул в единице объёма,  — средняя скорость молекул и l — длина свободного пробега молекулы между двумя соударениями её с другими молекулами.

Теплопроводность:

где r-плотность, С_V - теплоемкость при постоянном объеме, -ср. скорость движения частиц, -длина своб. пробега частиц. теплопроводность к. Т пропорциональна 1/р, а r~p (р- давление газа), теплопроводность идеального газа не зависит от р.

Коэффициент диффузии – количественная характеристика скорости диффузии, равная количеству вещества (в массовых единицах), проходящего в единицу времени через участок единичной площади (например, 1м²) при градиенте концентрации, равном единице (соответствующем изменению 1 моль/л → 0 моль/л на единицу длины)

_15. Планетарная модель атома, опыты Резерфорда. Постулаты Бора, Боровский радиус. Расчет уровней энергии электрона в атоме водорода.

Резерфорд предложил планетарную модель атома. Согласно этой модели, в центре атома располагается положительно заряженное ядро, в котором сосредоточена почти вся масса атома. Атом в целом нейтрален. Вокруг ядра, подобно планетам, под действием кулоновских сил со стороны ядра вращаются электроны (рис. 6.1.4). Находиться в состоянии покоя электроны не могут, так как они упали бы на ядро.

Планетарная модель атома, предложенная Резерфордом, несомненно явилась крупным шагом вперед в развитии знаний о строении атома. Она была совершенно необходимой для объяснения опытов по рассеянию α-частиц, однако оказалась неспособной объяснить сам факт длительного существования атома, т. е. его устойчивость. По законам классической электродинамики, движущийся с ускорением заряд должен излучать электромагнитные волны, уносящие энергию. За короткое время (порядка 10^–8 с) все электроны в атоме Резерфорда должны растратить всю свою энергию и упасть на ядро. То, что этого не происходит в устойчивых состояниях атома, показывает, что внутренние процессы в атоме не подчиняются классическим законам.

опыты Резерфорда и его сотрудников привели к выводу, что в центре атома находится плотное положительно заряженное ядро, диаметр которого не превышает 10^–14–10^–15 м. Это ядро занимает только 10^–12 часть полного объема атома, но содержит весь положительный заряд и не менее 99,95 % его массы. Веществу, составляющему ядро атома, следовало приписать колоссальную плотность порядка ρ ≈ 10¹⁵ г/см³. Заряд ядра должен быть равен суммарному заряду всех электронов, входящих в состав атома. Впоследствии удалось установить, что если заряд электрона принять за единицу, то заряд ядра в точности равен номеру данного элемента в таблице Менделеева.

Сам опыт:

От радиоактивного источника, заключенного в свинцовый контейнер, α-частицы направлялись на тонкую металлическую фольгу. Рассеянные частицы попадали на экран, покрытый слоем кристаллов сульфида цинка, способных светиться под ударами быстрых заряженных частиц. Сцинтилляции (вспышки) на экране наблюдались глазом с помощью микроскопа. Наблюдения рассеянных α-частиц в опыте Резерфорда можно было проводить под различными углами φ к первоначальному направлению пучка. Было обнаружено, что большинство α-частиц проходит через тонкий слой металла, практически не испытывая отклонения. Однако небольшая часть частиц отклоняется на значительные углы, превышающие 30°. Очень редкие α-частицы (приблизительно одна на десять тысяч) испытывали отклонение на углы, близкие к 180°.