§ 4.2. Мцстяви эярэинлик вязиййяти
Лювщянин
эярэинлик вязиййяти о вахт мцстяви
эярэинлик вязиййяти адланыр ки,
отураъаглара паралел кясиклярдя
эярэинлик вектору бцтцн щяъм бойу сыфыра
бярабяр олур. Галынлыьы
олан лювщянин орта мцстявисини координат
мцстявиси щесаб едяк. Онда тярифя эюря
.
Она эюря дя таразлыг тянликляри
(4.12)
шяклиня дцшцр.
олдуьундан
Бурадан
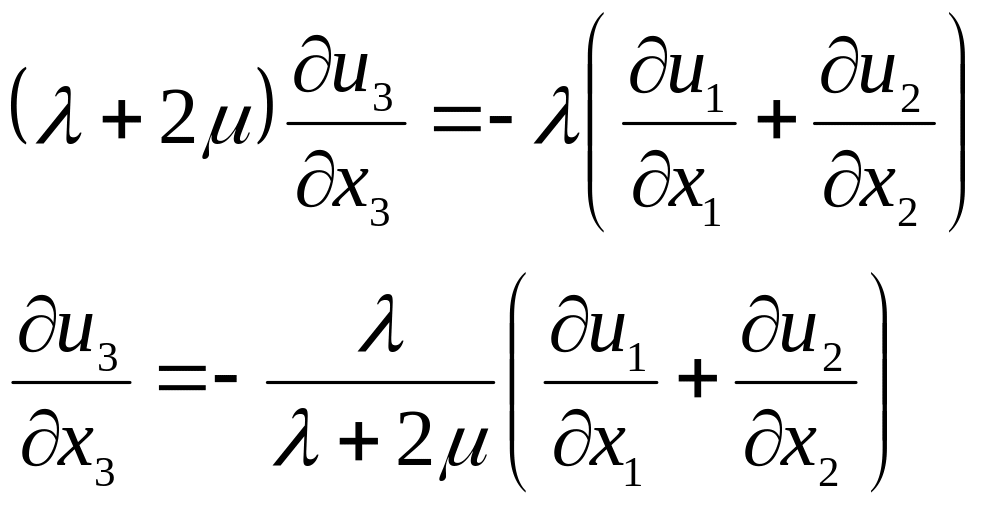
Онда
(4.13)
Бурада
Ейни гайда иля
(4.14)
Щук ганунундан
(4.15)
Эюрцндцйц
кими (4.2) вя (4.3) тянликляри мцстяви
деформасийа тянликляриндян
ны
иля явяз етмякля алыныр (4.4)-ц Ляме
тянликляриндя нязяря алсаг
(4.16)
Бу тянликляр Ляме тянликляриндян йалныз ны -ла явяз олунмасы иля фярглянир.
Беляликля мцстяви эярэинлик вязиййятинин тянликляринин ящямиййятли дяряъядя садяляшмясиня бахмайараг бу мясяля цч юлчцлц олараг галыр, чцнки дяйишяни тянликлярдя галыр. Лакин лювщя назик диварлы олдугда цчцнъц координаты, йяни ц тянликлярдян чыхармаг олур. Бу щал цмумиляшмиш эярэинлик вязиййяти адланыр.
§ 4.3. Цмумиляшмиш мцстяви эярэинлик вязиййяти
Фярз едяк ки, галынлыьы олан лювщя отураъагларына паралел вя орта мцстявийя симметрик олан, йан сятщлярдя тясир едян йцклярин тясири алтындадыр. Лювщянин отураъаглары йцкдян азаддыр. Щямчинин фярз едяк ки, кцтля гцввяляринин орта мцстявийя перпендикулйар олан топлананы сыфырдыр, диэяр топлананлар ися орта мцстявийя симметрикдир. Беля лювщядя йаранан эярэинлик вязиййяти цмумиляшмиш мцстяви эярэинлик вязиййяти адланыр.
Шяртя
эюря отураъагларда
(
)
(4.17)
Йан
сятщлярдя
.
Бундан башга
.
Бурада
сятщи
гцввялярин компонентляридир. Таразлыг
тянликляринин цчцнъцсцндя, йяни
тянлийиндя
(4.1) шяртини нязяря алсаг
да
аларыг.
Беляликля
да
няинки
эярэинлийинин юзц, щям дя онун
я
эюря тюрямяси сыфыр олур. Она эюря дя
кифайят гядяр кичик галынлыгларда
цн
гиймяти бцтцн галынлыг бойу кичик олаъаг
вя биз щесаб едяъяйик ки, бцтцн лювщя
бойу
.
Симметриклийя
эюря ашкардыр ки, орта мцстявисинин
истянилян нюгтянин йердяйишмясинин
охуна пройексийасы сыфыра бярабярдир
вя
я
нязярян тяк функсийадыр, она эюря дя
онун орта гиймяти
.
Щесаб
едяъяйик ки,
вя
пройексийлары кясилмяз функсийалардыр,
она эюря дя галынлыг бойу аз дяйиширляр
вя биз
,
явязиня онларын галынлыг бойу ашаьыдакы
орталашмыш гиймятлярини эютцряъяйик
[1].
(4.18)
Бахылан щал цчцн таразлыг тянликляри ашаьыдакы кими олур.
(4.19)
(4.3)
системинин тянликляринин щяр тяряфини
вуруб,
а
бюляк вя
дан
а
гядяр интеграллайаг. (4.1) шяртиня эюря
Онда олдуьуну да нязяря алсаг (4.3)-дян
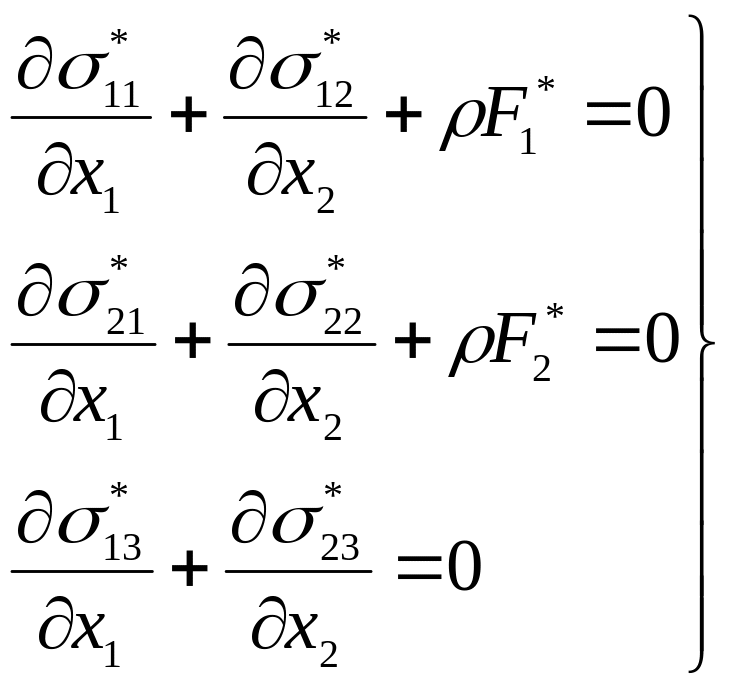(4.20)
(4.21)
аларыг.
Бурада
нин
галынлыг бойу орталашмыш гиймятляридир.
Цмумиляшмиш мцстяви эярэинлик вязиййятинин
тярифиндян чыхыр ки,
я
нязярян ъцт,
ися
тяк функсийалардыр. Она эюря дя
вя
цн
орта гиймятляри сыфыра бярабярдирляр
вя (4.5) бярабярlийи
ейниликдир. Йан сятщлярдяки сярщяд
шяртлярини дя
я
нязярян орталашдырсаг аларыг:
(4.22)
бурада
Щук ганунун дцстурларында я эюря орталашдырма апараг
(4.23)
Бурада
(4.4),
(4.6) вя (4.7) мцнасибятляри мцстяви
деформасийанын уйьун мцнасибятляриндян
анъаг онунла фярглянирляр ки, эярэинлик
вя деформасийалар онларын
я
эюря орталашмыш гиймятляри иля вя
сабити
сабити иля явяз олунурлар.
Беляликля ашаьыдакы ясас нятиъя алыныр. Мащиййятъя мцхтялиф олан мцстяви деформасийа вя цмумиляшмиш мцстяви эярэинлик вязиййятляри мясяляляри рийази ъящятдян идентикдирляр.