
- •§ 1.2. Даь сухурларында эярэинликляр
- •§ 1.3. Баш эярэинликляр, баш охлар
- •§ 1.4. Ъисмин щярякятинин дифференсиал тянликляри
- •§ 2.1. Деформасийаларла йердяйишмяляр арасында ялагя
- •§ 2.2. Цмумиляшмиш Щук гануну
- •§ 2.3. Еластики деформасийанын потенсиал енержиси
- •§ 3.1. Ляме тянликляри
- •§ 3.2. Гейри мящдуд еластики мцщитдя бойуна
- •§ 4.1. Мцстяви деформасийа
- •§ 4.2. Мцстяви эярэинлик вязиййяти
- •§ 4.3. Цмумиляшмиш мцстяви эярэинлик вязиййяти
- •§ 4.4. Ери эярэинлик функсийасы
- •§ 4.5. Мцстяви мясялянин полйар координатларда цмуми тянликляри
- •§ 4.6. Полйар координатларда Ери функсийасы Ляме мясяляси
- •§ 5.1. Лимит эярэинлик вязиййятинин ясас щипотезляри
- •§ 5.2. Йени енерэетик мющкямлик шярти. Ахма сятщи
- •§ 5.3. Даь сухурларынын сцртцнмядян йейилмяси
- •§ 5.4. Даь сухурларынын йорьунлугдан даьылмаьа щесабы
- •§ 6.1. Даь сухурлары сынагларынын садя нювляри
- •§ 6.2. Минералларын деформасийа олунма хцсусиййятляри вя механики хассяляринин эюстяриъиляри
- •§ 6.3. Даь сухурларынын еластики хассяляринин эюстяриъиляри
- •§ 6.4. Даь сухурларынын мющкямлик эюстяриъиляри
- •§ 6.5. Щяртяряфли сыхылмада даь сухурлары
- •§ 6.6. Даь сухурларынын мцнтязям щяртяряфли сыхылмасы. Сухурларын сыхылма ямсалы.
- •§ 6.7. Даь сухурларынын гейри-мцнтязям сыхылмасы
- •§1.2. Даь сухурларында эярэинликляр…………………….9
- •§ 1.2. Gярэинликляр.
- •§ 1.3. Баш эярэинликляр, баш охлар
- •§ 1.4. Ъисмин щярякятинин дифференсиал тянликляри
- •§ 2.1. Деформасийаларла йердяйишмяляр арасында ялагя
- •§ 2.2. Цмумиляшмиш Щук гануну
- •§ 2.3. Еластики деформасийанын потенсиал енержиси
- •§ 3.1. Ляме тянликляри
- •§ 3.2. Гейри мящдуд еластики мцщитдя бойуна
- •§ 4.1. Мцстяви деформасийа
- •§ 4.2. Мцстяви эярэинлик вязиййяти
- •§ 4.3. Цмумиляшмиш мцстяви эярэинлик вязиййяти
- •§ 4.4. Ери эярэинлик функсийасы
- •§ 4.5. Мцстяви мясялянин полйар координатларда цмуми тянликляри
- •§ 4.6. Полйар координатларда Ери функсийасы Ляме мясяляси
Əsas fərziyyələr.
«
Бярк ъисим механикасынын ян садя мясяляляринин беля щялли бюйцк рийази чятинликлярля баьлы олур. Бу чятинликляри арадан галдырмаг цчцн бярк ъисмин хассяляри барядя практикада юзцнц йахшы доьрулдан ашаьыдакы фярзиййяляр гябул едилир [11].
Щесаб едилир ки, бярк ъисим бцтювдцр, йяни онун айры-айры атом вя молекуллардан ибарят олдуьу нязяря алынмыр. Бу фярзиййя кясилмяз функсийалар нязяриййясинин бярк ъисим механикасы мясяляляринин щяллиня тятбиг олунмасына имкан верир.
Щесаб едилир ки, даь сухуру изотропдур, йяни онун бцтцн истигамятлярдя механики хассяляри ейнидир. Даь сухурларынын айры-айры лайлардан ибарят щиссясиня бахылдыгда о анизотроп щесаб едилир, йяни щесаб едилир ки, мцхтялиф истигамятлярдя даь сухурларынын механики хассяляри мцхтялифдир.
Щесаб едилир ки, даь сухуру биръинсдир, йяни онун механики хассяляри нюгтядян нюгтяйя дяйишмир вя бцтцн нюгтялярдя ейнидир.
Щесаб едилир ки, хариъи гцввяляр тясир етмирся дахили эярэинликляр дя йохдур, йяни дахили эярэинликляр хариъи гцввялярин тясириндян йараныр. Айры-айры щалларда, чох бюйцк дяринликлярдя йерляшян даь сухурларына бахдыгда даь сухурларынын юзцнцн йаратдыьы тязйиг башланьыъ эярэинликляр кими нязяря алыныр.
Щесаб олунур ки, еластиклик щцдуду дахилиндя бярк ъисмя тясир едян гцввяляр системинин нятиъяси айры-айры гцввялярин нятиъяляри ъяминя бярабяр олур вя бу гцввялярин тятбиг олунма ардыъыллыьындан асылы олмур (гцввялярин тясирляринин асылы олмамасы принсипи). Гейд етмяк лазымдыр ки, пластик деформасийалар оларкян бу фярзиййя практикада юзцнц доьрултмур, йяни йаранан пластик деформасийалар хариъи гцввялярин тясиретмя ардыъыллыьындан асылы олур.
Сен-Венан принс ипи. Щесаб едилир ки, хариъи гцввялярин тятбиг нюгтяляриндян кифайят гядяр узаглыгда дахили эярэинликлярин пайланмасы хариъи гцввялярин конкрет тятбигедилмя формасындан асылы дейил. Сен-Венан принсипи сярщяд шяртляринин садяляшдирилмясиня имкан верир. Мисал цчцн ашаьыдакы мясяляни нязярдян кечиряк. Тутаг ки, бир уъундан бяркидилмиш чубуьун диэяр уъунда биринъи щалда тапа
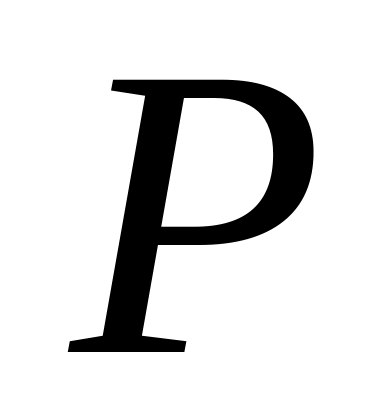 гцввяси, икинъи щалда ися сяпялянмиш
гцввяси, икинъи щалда ися сяпялянмиш
 гцввяси тятбиг едилмишдир. Бурада
гцввяси тятбиг едилмишдир. Бурада
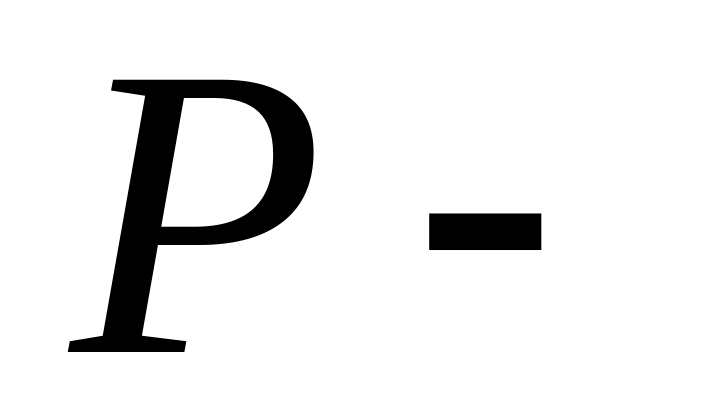 ващид
ен кясик сащясиня тясир едян гцввя,
ващид
ен кясик сащясиня тясир едян гцввя,
 ен
кясик сащясидир (шякил 1а).
ен
кясик сащясидир (шякил 1а).
Ш
Шякил
1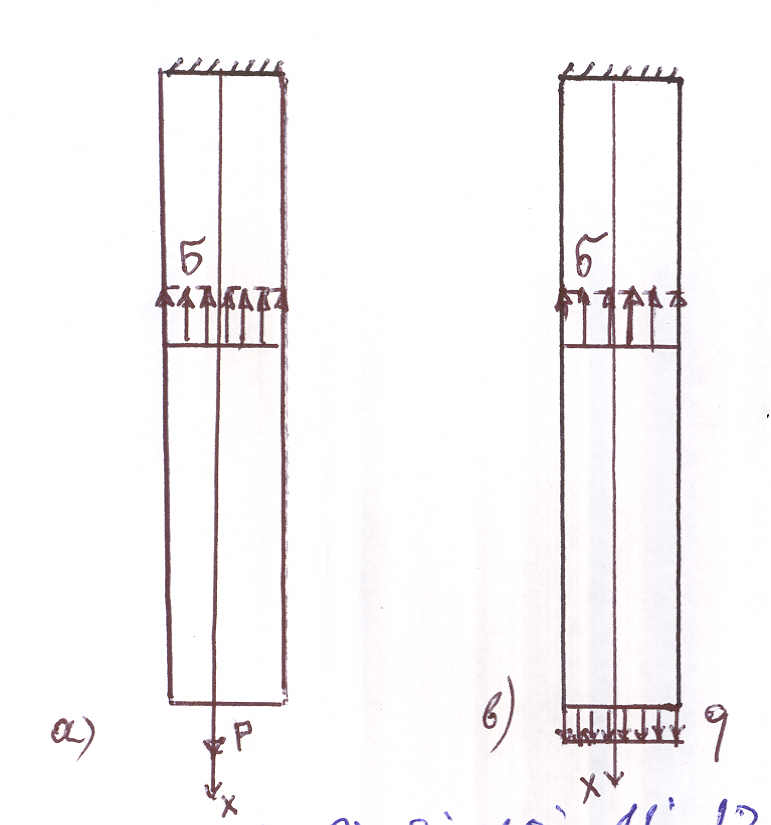
![]() нюгтясиндя, шякил 1-дя ися
нюгтясиндя, шякил 1-дя ися
![]() нюгтясиндя эютцрцб Х охуну ашаьыйа
йюнялтсяк
нюгтясиндя эютцрцб Х охуну ашаьыйа
йюнялтсяк
![]() дя
шякил а-да хариъи гцввя сычрайышла
дяйишир вя ону рийази моделляшдирмяк
чох чятиндир. Шякил б-дя хариъи гцввя
мцнтязям пайланмышдыр вя сярщяд шярти
чох садядир (
дя
шякил а-да хариъи гцввя сычрайышла
дяйишир вя ону рийази моделляшдирмяк
чох чятиндир. Шякил б-дя хариъи гцввя
мцнтязям пайланмышдыр вя сярщяд шярти
чох садядир (![]() ).
).
Сен-Венан принсипиня эюря ашаьы уъдан хейли узаглашдыгда (2-3 диаметря бярабяр мясафядя) дахили эярэинликляр ейни ъцр пайланыр.
Мцшащидяляр эюстярир ки, тсиклик йцклянмядя бярк ъисимляр бир дяфя йцклянмядякиндян хейли кичик гцввялярин тясириндян даьылырлар. Беля щадися бярк ъисим материалынын йорьунлуьу адланыр. Щям дя ъисим тсикллярин сайы артдыгъа даща кичик гцввялярин тясириндян даьылыр. Бярк ъисимляр цчцн ашаьыдакы механики моделляр мювъуддур [13].
Еластики ъисим, йахуд Щук ъисми бу моделя эюря ъисимляр даьылана гядяр еластики галырлар. Беля ъисимляр кювряк ъисимляр адланырлар (шякил 2 а).
Идеал еластик-пластик ъисимляр. Бу моделя табе олан ъисимляр яввялъя еластики деформасийа олунурлар, сонра ися сабит эярэинлик алтында пластик деформасийайа уьрайырлар (шякил 2 б).
Идеал сярт-пластик ъисимляр. Беля ъисимляр эярэинлийин ахма щяддиня гядяр юзлярини мцтляг бярк ъисим кими апарырлар, йяни деформасийа олунмурлар, эярэинлик ахма щяддиня чатдыгда ися сабит эярэинлик алтында пластики деформасийа олунурлар (шякил 2).
Юзцлц ъисимляр, йахуд Нйутон ъисми. Беля ъисимляр юзцлц майеляр кими деформасийа олунурлар (шякил 3).

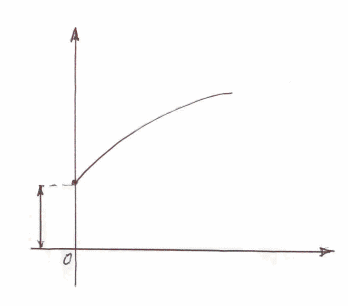
Шякил
2-дя
![]() бирохлу
дартылмада нормал эярэинлик
бирохлу
дартылмада нормал эярэинлик
![]() нисби
деформасийа,
нисби
деформасийа,
![]() ахма
эярэинлийидир.
ахма
эярэинлийидир.
![]()
![]()
![]()
Шякил
3-дя
![]() ани
нисби деформасийа,
заман
кечдикъя йаранан нисби деформасийа,
ани
нисби деформасийа,
заман
кечдикъя йаранан нисби деформасийа,
![]() замандыр.
замандыр.
Йухарыда ады чякилян дюрд моделин комбинасийасы кими истянилян бярк ъисимин моделини гурмаг олар.
§ 1.2. Даь сухурларында эярэинликляр
Биз ясасян даща садя вя практикада эениш тятбиг олунан еластики бярк ъисим моделиня бахаъаьыг. Щесаб едяъяйик ки, ъисим идеал еластикидир, йяни эярэинлик вя деформасийалар арасында асылылыг хяттидир вя мясялялярин щяллиндя гцввялярин тясирляринин асылы олмамасы принсипини тятбиг етмяк олар.
Материаллар мцгавимяти курсундан мялумдур ки, верилмиш нюгтядян кечян кясикдяки эярэинликляр кясийин орийентасийасындан асылыдырлар. Верилмиш нюгтядян кечян бцтцн мцмкцн кясикдяки эярэинликляр топлусу нюгтядяки эярэинлик вязиййяти адланыр. Цмуми йцклянмя щалларында мцряккяб мясялялярин щяллиндя, хцсусян дя мющкямлийя щесабатда нюгтядя эярэинлик вязиййятинин дяйишмясиндян эениш истифадя едилир.

Тутаг ки, еластики ъисим ихтийари гцввяляр системинин тясири алтындадыр. Нюгтядян нюгтяйя кечяркян эярэинлик вязиййяти чох аз дяйишир вя щямишя бахылан нюгтянин еля кичик ятрафыны эютцрмяк олар ки, бу ятрафда эярэинлик вязиййятини биръинс щесаб етмяк олсун.
Верилмиш
![]() нюгтясиндя эярэинлик вязиййятини
характеризя етмяк цчцн бу нюгтядян цч
гаршылыглы перпендикулйар кясик кечириб
бу кясикдяки эярэинликляри тяйин едяк.
Даща сонра
нюгтясини юз дахилиндя сахлайан елементар
паралелепипед айыраг (шякил 4). Яэяр
паралелепипедин юлчцлярини кичилтсяк
о
нюгтясиня йыьылар. Лимит вязиййятиндя
бцтцн цзляр
нюгтясиндян кечир вя цзлярдяки
эярэинликляря
нюгтясиндяки эярэинликляр кими бахылыр.
Щяр бир кясикдяки эярэинлик цч топланана
айрылыр. Кясийин нормалы бойу йюнялян
топланан нормал эярэинлик адланыр вя
нюгтясиндя эярэинлик вязиййятини
характеризя етмяк цчцн бу нюгтядян цч
гаршылыглы перпендикулйар кясик кечириб
бу кясикдяки эярэинликляри тяйин едяк.
Даща сонра
нюгтясини юз дахилиндя сахлайан елементар
паралелепипед айыраг (шякил 4). Яэяр
паралелепипедин юлчцлярини кичилтсяк
о
нюгтясиня йыьылар. Лимит вязиййятиндя
бцтцн цзляр
нюгтясиндян кечир вя цзлярдяки
эярэинликляря
нюгтясиндяки эярэинликляр кими бахылыр.
Щяр бир кясикдяки эярэинлик цч топланана
айрылыр. Кясийин нормалы бойу йюнялян
топланан нормал эярэинлик адланыр вя
![]() иля ишаря едилир. Кясик цзяриндяки
топлананлар тохунан эярэинликляр
адланырлар вя
иля ишаря едилир. Кясик цзяриндяки
топлананлар тохунан эярэинликляр
адланырлар вя
![]() иля ишаря едилирляр.
иля ишаря едилирляр.
Паралелепипедин эюрцнмяйян цзяриндя дя ейни ъцр эярэинликляр йараныр, лакин якс тяряфляря йюнялирляр.
Елементя
тясир едян гцввяляр системи таразлыг
шяртлярини юдямялидирляр. Эюрцнмяйян
цзлярдя йаранан гцввяляр эюрцнян
цзлярдяки гцввялярин яксиня йюнялдийиндян
таразлыьын биринъи цч шярти ейнилик
кими юдянир, йяни тясир едян гцввялярин
![]() охларына пройексийалары ъями сыфыра
бярабяр олур. Бцтцн гцввялярин
охларына нязярян моментляри ъяминин
сыфыра бярабяр олмасы шяртини йохлайаг.
Шякил 4-дян эюрцндцйц кими нормал
гцввялярин истянилян оха нязярян
моментляри ъями сыфыра бярабяр олур.
Тохунан гцввялярин
охларына пройексийалары ъями сыфыра
бярабяр олур. Бцтцн гцввялярин
охларына нязярян моментляри ъяминин
сыфыра бярабяр олмасы шяртини йохлайаг.
Шякил 4-дян эюрцндцйц кими нормал
гцввялярин истянилян оха нязярян
моментляри ъями сыфыра бярабяр олур.
Тохунан гцввялярин
![]() охуна нязярян моментляри ъяминин сыфыра
бярабяр олмасы цчцн
охуна нязярян моментляри ъяминин сыфыра
бярабяр олмасы цчцн
![]() кясийиндяки
кясийиндяки
![]() гцввясинин
охуна нязярян моменти (бу гцввянин
охуна нязярян голу
гцввясинин
охуна нязярян моменти (бу гцввянин
охуна нязярян голу
![]() дир)
дир)
![]() кясийиндяки
кясийиндяки
![]() гцввясинин
охуна нязярян моментиня бярабяр олмалыдыр
(бу гцввянин
охуна нязярян голу
гцввясинин
охуна нязярян моментиня бярабяр олмалыдыр
(бу гцввянин
охуна нязярян голу
![]() я
бярабярдир), йяни
я
бярабярдир), йяни
![]()
аналожи шяртлярдян
![]() (1.1)
(1.1)
алыныр.
Беляликля (1)-дян эюрцндцйц кими гаршылыглы перпендикулйар цзлярдяки тохунан эярэинликляр гиймятъя бярабяр олуб йа цмуми тиля йа да цмуми тилдян йюнялирляр. Бу материаллар мцгавимятиндян билдийимиз тохунан эярэинликлярин ъцтлцйц ганунудур. Тохунан эярэинликлярин ъцтлцйц нятиъясиндя нюгтядяки эярэинлик компонентляринин сайы 9-дан 6-йа енир.
Инди
ися истянилян вязиййятдяки кясикдяки
эярэинлик вязиййятини тяйин едяк. Бунун
цчцн
нюгтяси ятрафында паралелепипед дейил
дюрдцзлц айыраг (шякил 5). Айрылан
елментин цч цзц координат мцстявиляри
иля цст-цстя дцшцр. Дюрдцнъц цз ися
ихтийари вязиййятдядир вя онун йюнялдиъи
косинусларыны
![]() нормалыны
нормалыны
![]() иля ишаря едяк. Юлчцляр кичилдикдя бцтцн
цзляр А нюгтясиндян кечир вя цзлярдяки
эярэинликляря нюгтядяки эярэинликляря
нюгтядяки эярэинликляр кими бахылыр.
иля ишаря едяк. Юлчцляр кичилдикдя бцтцн
цзляр А нюгтясиндян кечир вя цзлярдяки
эярэинликляря нюгтядяки эярэинликляря
нюгтядяки эярэинликляр кими бахылыр.
Ш
Шякил
5
![]() эярэинлик векторунун
охларына пройексийаларыны
эярэинлик векторунун
охларына пройексийаларыны
![]() иля ишаря едяк. Бу цч кямиййят мялум
оларса истянилян вязиййятдяки нормал
вя тохунан эярэинликляр тапыла биляр.
БЪД цчбуъаьынын сащясини-Ф,
иля ишаря едяк. Бу цч кямиййят мялум
оларса истянилян вязиййятдяки нормал
вя тохунан эярэинликляр тапыла биляр.
БЪД цчбуъаьынын сащясини-Ф,
![]() нинкини
-
нинкини
-![]() ,
,
![]() нинкини
нинкини
![]() ,
АБЪ-нинкини-
,
АБЪ-нинкини-![]() иля ишаря едяк. Мялумдур ки, [12].
иля ишаря едяк. Мялумдур ки, [12].
![]() (1.2)
(1.2)
Елементя
тясир едян бцтцн гцввяляри
![]() охларына пройексийаласаг аларыг
охларына пройексийаласаг аларыг
![]() (1.3)
(1.3)
(1.2)-ни (1.3)-дя нязяря алсаг
![]() (1.4)
(1.4)
Беляликля верилмиш нюгтядян кечян истянилян цч гаршылыглы перпендикулйар кясикдя тясир едян 6 эярэинлик компоненти мялум оларса щямин нюгтядян кечян истянилян ориентасийалы кясикдяки эярэинликляри (1.4) дцстурларынын кюмяйи иля тяйин етмяк олар.
