25. Алгоритмы на графах, решение задачи о минимальной телефонной сети, построение минимального оставного дерева
Задача о min-ой телефонной сети
Дана плоская страна и в ней n-городов. Нужно соединить все города, чтобы общая длина телефонной линии связи была min-ой.
Уточнения:
-города пренебрежительно малы
-подразумевается эффективность связи
-транзитивность связи
-нет циклов
-рефлективность.
Дан полный взвешенный граф с n-вершинами. Найти min-ое оставное дерево (МОД) этого графа.
Петля-ребро, ведущее из вершины в нее же.
Простой граф — граф без кратный ребер и петель.
Цепь — последовательность ребер, ведущий из одной вершины в другие
Связный граф — граф, в котором существует цепь или путь между 2 любыми вершинами.
Взвешенный граф — сеть.
Подграф — часть вершины и все инцидентные им ребра.
Суграф — все вершины и часть инцидентных им ребер.
Дерево — граф без циклов.
Остовное дерево — связный суграф, не имеющий циклов.
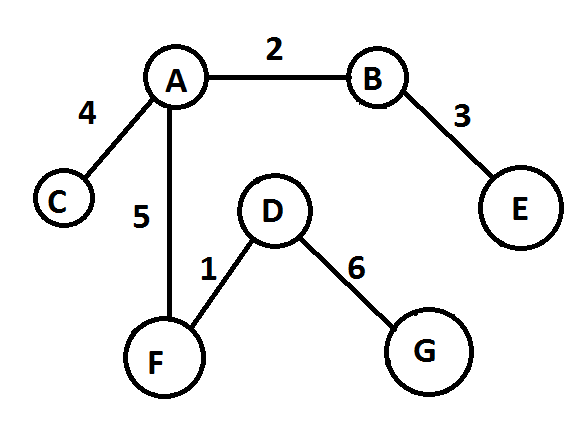
Пусть имеется граф Т, определяемый множеством вершин и множеством ребер: T(V,E). Начинаем с T1(V,Е). Каждая вершина в такой ситуации связана лишь с собой. В процессе выполнения, имея набор связных компонент формируем остовное дерево. Поочередно проверяются ребра из мн-ва E, в порядке возрастания вес. коэф. И если очередное ребро связывает 2 вершины из разных компонент, то его добавляют, а если 2 вершины из одной компонент, то отбрасывают. Когда все вершины будут принадлежать одной компоненте, то дерево построено. В начале дано V={T,E}. Построим min-ое оставное дерево 1+2+3+4+5+6=21
