2.4 . Основные виды входных воздействий
В теории управления техническими системами принят ряд стандартных входных воздействий, по реакции на которые определяются динамические свойства (характеристики) системы управления (звена). К таким воздействиям относятся: единичное импульсное воздействие, единичное ступенчатое воздействие, единичное гармоническое воздействие, линейное воздействие и др. Рассмотрим их более подробно…
2.4.1. Единичное ступенчатое воздействие
Данное воздействие является одним из наиболее «жестких» (неблагоприятных) воздействий, по реакции на которое сравниваются переходные свойства (переходной процесс) идентичных или близко идентичных систем.
Реакция системы (звена) на такое воздействие называется переходной функцией.
Единичное ступенчатое воздействие обозначается 1(t) и бывает 3-х видов: два асимметричных и одно симметричное.
1(t)
(2.4.1)
Рассмотрим каждый из этих видов:
а) б) в)
Рисунок 2.8 – Графики единичных ступенчатых воздействий
В
теории управления наибольшее
распространение имеет асимметричное
воздействие 1+
(t),
поскольку принято, что при t
0 САР находится в
равновесии, и анализ переходных процессов
ведется только при
t
0.
Для удобства представления будем в дальнейшем записывать воздействие 1+(t), опуская индекс. 1+ (t) 1(t).
Поскольку рассматриваемое входное воздействие имеет разрыв при t = 0 (что иногда нежелательно в численных алгоритмах, использующих конечно-разностную схему), имеется формула, позволяющая приближенно описать единичное ступенчатое воздействие:
1(t)
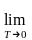(1
– e
–t/T)
,
(2.4.2)
где Т – постоянная
времени, а текущее время
!!!
На рисунке 2.9 представлена графическая иллюстрация аппроксимации 1(t) по формуле (2.4.2).
t
T 1 T 2 T 3
Рисунок 2.9 – Графики аппроксимаций единичного ступенчатого воздействия
2.4.2. Единичное импульсное воздействие: - функция Дирака
В курсе «Математика» различают три вида данного воздействия: одно симметричное и два асимметричных.
Рассмотрим все эти воздействия
Симметричное единичное импульсное воздействие (t) определено как:
0, если t
0
(t)
= ,
если t
= 0
;
0, если t 0
Графическая иллюстрация симметричного единичного импульсного воздействия представлена на рисунке 2.10. Фактически (t) – импульс (с длительностью стремящейся к нулю и амплитудой, равной бесконечности), площадь которого равна 1. .
а) б) в)
Рисунок 2.10 – Варианты представления симметричного импульсного воздействия
Для симметричного единичного импульсного воздействия (t) существует аналитическая форма представления:
(t)
=
;
Покажем, что интеграл равен 1, 0
,
где
u
= ht
и
- интеграл ошибок равный
.
Смещенные (асимметричные) единичные импульсные воздействия определяются как:
где - сколь угодно малое положительное число ( 0).
Графическая
иллюстрация смещенных единичных
импульсных воздействий
представлена на рисунке 2.11.
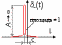
а) б)
Рисунок 2.11 – Смещенные единичные импульсные воздействия
Внимание.
В дальнейшем в курсе «УТС» будет
использоваться только
+
(t).
Индекс «+» опускается…
+
(t)
(t).
Поскольку смещенное единичное импульсное воздействие фактически имеет разрыв при t = 0 (что иногда нежелательно в численных алгоритмах, использующих конечно-разностную схему), имеется формула, позволяющая приближенно описать смещенное единичное импульсное воздействие:
,
(2.4.3)
где Т – постоянная времени, а текущее время !!!
На рисунке 2.12 представлена графическая иллюстрация аппроксимации (t) по формуле (2.4.3).
(t)
t
T 1 T 2 T 3
Рисунок 2.12 – Графики аппроксимаций единичного импульсного воздействия
Реакция САУ (звена) на воздействие (t) называется весовой функцией.