2.2. Линеаризация уравнений динамики сау (сар)

Практически все реальные системы автоматического управления (САУ) являются нелинейными, причем нелинейность САУ может определяться различным причинами:

1) Нелинейностью статической характеристики.

2) Нелинейностью динамических членов в уравнениях динамики.

3) Наличием в САУ принципиально нелинейных звеньев.

Если в замкнутой САУ (САР) нет принципиально нелинейных звеньев, то в большинстве случаев уравнения динамики звеньев, входящих в систему, могут быть линеаризованы. Линеаризация основана на том, что в процессе регулирования (т.е. САУ с обратной связью) все регулируемые величины мало отклоняются от их программных значений (иначе система регулирования или управления не выполняла бы своей задачи).

Например, если рассмотреть управление мощностью энергетического ядерного реактора, то главная задача САР - поддержание мощности на заданном (номинальном) уровне мощности. Существующие возмущения (внутренние и внешние) “отрабатываются” САР и поэтому параметры ядерного реактора незначительно отличаются от стационарных. На рис. 2.5 представлена временная зависимость мощности ядерного реактора, где нормированные отклонения мощности N /N₀ << 1, и поэтому уравнения динамики ядерного реактора, в принципе, могут быть линеаризованы.

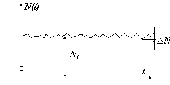
Рис. 2.5

Рассмотрим некоторое звено (или САР в целом), описание динамики которого можно представить в переменных “вход-выход”. Предположим, что динамика данного звена описывается обыкновенным дифференциальным уравнением n-го порядка:

. (2.2.1)

Перенесем в левую часть уравнения и запишем уравнение в виде

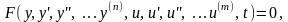(2.2.2)

где F – функция регулируемой переменной и ее производных, а также управляющего (входного) воздействия и его производных, причем F – обычно нелинейная функция.

Будем считать, что при t £ 0 САУ (звено) находилось в равновесии (в стационарном состоянии). Тогда уравнение (2.2.2) вырождается в уравнение статической характеристики.

(2.2.3)

Разложим левую часть уравнения (2.2.2) в ряд Тейлора в малой окрестности точки равновесного состояния (y₀, u₀).

Напомним, что в курсе “Математика” разложение в ряд Тейлора трактуется следующим образом.  Если y = f(x), то «простое» разложение в ряд Тейлора в окрестности точки x = x₀ равно:

C учетом вышеприведенного разложение принимает вид:

Предполагая, что отклонения выходных и входных воздействий незначительны (т.е. ), оставим в разложении только члены 1-го порядка малости (линейные). Поскольку получаем:

(2.2.4)

Подставляя соотношение (2.2.4) в уравнение (2.2.2), после преобразований имеем:

Коэффициенты - постоянные коэффициенты, поэтому уравнение (2.2.5) - линейное обыкновенное дифференциальное уравнение с постоянными коэффициентами.

Еще раз напомним, что в дальнейшей части курса “УТС” будет часто использоваться операторная форма записи уравнений динамики:

(2.2.6)

где p = d / dt – оператор дифференцирования;

- линейный дифференциальный оператор степени n;

N(p) - линейный дифференциальный оператор степени m, причем обычно порядок оператора L(p) выше порядка оператора N(p).  n  m.

Уравнения (2.2.5) и (2.2.6) - уравнения динамики системы (звена) в отклонениях.

Если исходное уравнение (2.2.1) - дифференциальное уравнение в физических переменных (температура, скорость, поток и т.д.), то размерность коэффициентов может быть произвольной (любой).

Переход к нормализованным отклонениям позволяет “упорядочить” размерность коэффициентов. 

В самом деле, разделив уравнение (2.2.5) на 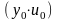и выполнив некоторые преобразования, получаем:

Приведение уравнения динамики САУ (звена) к нормализованному виду позволяет “унифицировать” размерность коэффициентов уравнений: 

Если вынести в правой части (2.2.7) коэффициент за общую скобку и разделить все уравнение на , то уравнение принимает вид:

Линеаризация уравнений динамики и, особенно, нормализация переменных позволяют привести уравнения динамики САУ (звена) к виду, наиболее удобному для использования классических методов анализа, т.е. к нулевым начальным условиям. 

Если t  0 

Пример: Выполнить линеаризацию уравнения динамики некоторой «абстрактной» САР в окрестности состояния (x ₀ , y ₀), если полное уравнение динамики имеет вид:

Нелинейность полного уравнения динамики проявляется в следующем:

• во-первых, в нелинейности статической характеристики

Рис. 2.6

• во-вторых, слагаемое в левой части - чисто нелинейное, так как действие умножение является нелинейным.

Внимание: выполним процесс линеаризации исходного уравнения динамики другим способом, основанным на том, что в окрестности состояния (x₀, y₀) нормированные отклонения управляющего воздействия и регулируемой величины намного меньше 1.

Преобразования выполним в следующей последовательности:

1) Перейдем к безразмерным переменным (нормализованным);

2) Выполним линеаризацию, отбросив нелинейные члены 2-го и выше порядков малости.

Перейдем к новым безразмерным координатам (переменным) 

Заметим, что

Подставляя значения x(t) и y(t) в исходное уравнение:

Подчеркнутые слагаемые - условия стационара. 



Если в правой части вынести за общую скобку и разделить все уравнение на , то уравнение (линеаризованное) принимает вид:

Процедура нормализации позволяет более просто линеаризовать уравнение динамики, так как не требуется выполнять разложение в ряд Тейлора (хотя это и не сложно).

Обобщая материал данного подраздела, необходимо отметить, что переход к безразмерным (нормализованным) отклонениям позволяет:

• во-первых, привести динамику САУ (звена) к нулевым начальным условиям;

• во-вторых, упрощает процесс линеаризации уравнения динамики, так как не требуется выполнять разложение в ряд Тейлора.