4.3. Перенос места обратной связи “вперед” или “назад”

а) вперед

Исходная САР

Эквивалентная САР

Wисх(s) = W1(s)_*W2(s)/(1+ Wос(s)_*W1(s))

Wэкв =W1(s)_* W2(s)/(1+ Wос(s)_*W1(s)W2(s)_*Z(s))

=> Z(s) = 1/ W2(s) (4.20)

б) назад

Исходная САР

Эквивалентная САР

Wисх(s) = W1(s)_*W2(s)/(1+ Wос(s)_*W1(s) _*W2(s))

Wэкв =W1(s) _*W2(s)/(1+ Wос(s)_*W1(s) _*Z(s))

Z(s) = W2(s) (4.21)

4.4 Перенос точек суммирования “вперед” или “назад”

а) вперед

Исходная схема Эквивалентная схема

Данные рисунки не требуют дополнительных комментариев

б) назад

Исходная схема Эквивалентная схема

Данные рисунки, также не требуют дополнительных комментариев

Иногда этот прием называется “перенос внешнего воздействия” =>

Если считать f(t) ≡ x₂(t), то это естественно!!!

4.5. Перенос точек ветвления сигнала “вперед” или “назад”

а) вперед

Исходная схема Эквивалентная схема

б) назад

Исходная схема Эквивалентная схема

Пример: Преобразовать структурную схему САР привести к единичной главной обратной связи.

Привести к виду

W_*(s)

x(t)

y(t)

Этапы преобразований:

1. W1+W2 =W9

2. W4,W5 => W10 =W4/(1+W4*W5)

3. W9 , W3 , W10 , W6 => W11 = W9*W3*W10*W6 =>

=

W11

W8

W7

> Wисх = W11_*W7 /(1+ W11_*W8) =

=W_* /(1+W_*)=>

W_**W7_*W11+ W11_*W7 = W_* + W_**W8_*W11

W7_*W11 = W_**[1+W8_*W11 − W11_*W7 ]=>

W_*(s) = W11_*W7/(1+ W11(W8 − W7))

5. Передаточные функции и уравнения динамики замкнутых систем автоматического регулирования (сар)

5.1. Главная передаточная функция. Передаточные функции по возмущающему воздействию и для ошибки (рассогласования)

Используя структурные преобразования (см. раздел 4), структурную схему практически любой линейной или линеаризованной САР (САУ) можно привести к виду:

Рис. 5.1

x (t) X (s) x (t) - управляющее воздействие;

y (t) .  Y (s) f (t) – возмущающее воздействие;

f (t)  F (s) y (t) – регулируемая величина (выходное воздействие).

 (t)  E (s)

Определение. Если единичная обратная связь охватывает все элементы (звенья) САР – она называется главной.

Если главная обратная связь отсутствует - САР считается разомкнутой.

Передаточная функция W(s) может быть любой сложности (т.е. содержать местные обратные связи, параллельные и последовательные цепи и т.д.).

Возмущающих воздействий может быть несколько и приложены они могут быть в любом месте структурной схемы.

Передаточную функцию W(s), которую в Теории Управления называют передаточной функцией разомкнутой САР, будем представлять в следующем виде (для единообразия):

(5.1)

где К – общий коэффициент усиления; N(s), L(s) – полиномы по степеням переменной s, причем свободные члены в них равны 1 (единице).

Учитывая, что САР линейна или линеаризована, разделим на структурной схеме каналы прохождения управляющего и возмущающего воздействий  Выделим в отдельное звено (может быть и очень сложное) ту часть системы, через которую проходит возмущающее воздействие f (t)  обозначим ее через M(s)  Структурная схема САР принимает вид:

Рис. 5.2

В Теории Управления используют 3 основных передаточных функций замкнутой САР:

• главная передаточная функция Ф(s);

• передаточная функция по возмущающему воздействию Ф_f (s) ;

• передаточная функция для ошибки (рассогласования )

Рассмотрим более подробно вышеупомянутые передаточные функции.

Главная передаточная функция (передаточная функция по управляющему воздействию)  Дадим математическое определение этой передаточной функции 

Ф (s) = , (5.2)

f(t) = 0

если  выведем формулу для Ф(s) 

x(t )  0

Поскольку главная передаточная функция определена соотношением (5.2) при условии, что возмущающее воздействие f(t) = 0, то  y(t) = y₁(t)  «обойдем» по контуру 

Y(s) = E(s)  W(s) =  X(s) – Y(s)   W(s)   1 + W(s)   Y(s) = W(s) X(s) ; 

Ф(s) = = (5.3)

Примечание. Формула (5.3) совпадает с формулой для передаточной функции цепи с местной единичной обратной связью (см. раздел 4 – «Структурные преобразования»).

Подставляя вместо W(s) ее выражение через полиномы N(s) и L(s) 

Ф(s) = (5.4)

Анализ выражение (5.3) показывает, что свойства главной передаточной функции замкнутой САР однозначно определяются свойствами разомкнутой САР, т.е. через полиномы N(s) и L(s).

Передаточная функция замкнутой САР по внешнему возмущающему воздействию

Дадим математическое определение рассматриваемой передаточной функции 

Ф_f (s) = , (5.5)

Очевидно, что у(t) = y₁(t) + y₂(t) 

Учитывая, что х(t) = 0;  (t) = 0 – y(t) = - y(t);  «обойдем» по контуру:

Y(s) = Y₁(s) +Y₂(s) = E(s) ∙W(s) + M(s) F(s) = W(s) -Y(s) + M(s) F(s) = M(s) F(s) - W(s) Y(s); 

[1 + W(s)]  Y(s) = M(s)  F(s);  Ф_f (s) = 

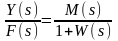
Ф_f (s) = = , (5.6)

где вид полинома R(s) - зависит от места приложения внешнего возмущающего воздействия;

Внимание. Формулы (5.4) и (5.6) имеют общие знаменатели, а именно: D(s) = L(s) + K N(s) !!!

Передаточная функция замкнутой САР для ошибки (рассогласования)

Данная передаточная функция определяется следующим выражением:

Ф_ (s) = 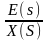, (5.7)

Сделаем вывод соответствующих формул, выполнив «обход» по контуру 

E(s) = X(s) - Y(s) = X(s) - E(s)W(s);  [1 + W(s)]  E(s) = X(s); 

Ф_ (s) = = 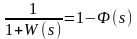, т.к. Ф(s) = . (5.8)

Подставляя в формулу (5.8) значение W(s) через полиномы N(s) и L(s), имеем 

Ф_ (s) = 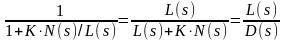. (5.9)

Опять замечаем, что знаменатель передаточной функции Ф_ (s) равен полиному D(s)  следовательно, характерным признаком передаточных функций замкнутой САР является общность знаменателей ! ! !.

В Теории Управления выражение D(s) = L(s) + K∙ N(s) имеет «собственное» название: характеристический полином замкнутой САР.

Если на САР воздействует одновременно два воздействия: x(t) и f(t), то 

Y(s) = Ф(s)X(s) + Ф_f (s)  F(s)  но об этом в следующем подразделе...