3.2.2. Идеальное дифференцирующее звено
=> Уравнение динамики звена имеет вид:
y(t)
= K∙τ∙x’(t),
где τ – постоянная времени.
Переходя к изображениям => x(t) X(s); x’(t) s∙X(s); y(t) Y(s) =>
Y(s) = K∙τ∙s∙X(s) – уравнение динамики звена в изображениях =>
W(s)
=
– передаточная функция
идеального дифференцирующего звена
АФЧХ => W(iω) = W(s)│s=iω = i∙ K∙τ∙ω => U(ω) = 0; V(ω) = K∙τ∙ω;
A(ω)
= mod W(iω)
= |W(iω)| =
K∙τ∙ω
=> φ(ω)
= const =
Графики годографа АФЧХ, A(ω) и φ(ω) имеют вид:
ЛАХ Lm(ω) = 20lg A(ω) = 20lg K + 20lg τ∙ω =>
=>
данное звено обеспечивает опережение
по фазе на π/2.
Чем выше частота единичного гармонического сигнала на входе в звено, тем выше амплитуда выходного сигнала в установившемся режиме.
Найдем весовую и переходную функции звена =>
w(t)
= Z -1[
]
= Z -1[K∙τ∙s]
=
[K∙τ∙
Z -1[1]] =
K∙τ
∙δ(t) =>
w(t) = K∙τ ∙δ’(t) =>
Учитывая, что δ(t) «утрировано» А весовая функция пропорциональна
имеет вид => см. ниже => производной от δ(t) => см. ниже
h(t) = Z -1[H(s)] =Z -1[ ] = Z -1[K∙τ ∙s/s] = K∙τ ∙δ(t)
h(t) = K∙τ ∙δ(t) =>
=>
Иногда ИДЗ представляется в виде W(s) = τ ∙s или W(s) = K∙s. В последнем варианте коэффициент К имеет смысл постоянной времени.
3.2.3. Идеальное интегрирующее звено
Уравнение динамики такого звена имеет вид:
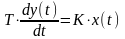=> в изображениях =>
–
уравнение динамики в изображениях =>
– передаточная функция
идеального интегрирующего звена.
АФЧХ => W(iω) = W(s)│s=iω = K /i∙T∙ω => W(iω) = K/i∙T∙ω => умножая на i =>
W(iω) = - i∙K/ T∙ω => U(ω) = 0; V(ω) = - K/T∙ω; => Годограф АФЧХ имеет вид:
=>
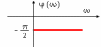
=> т.е. данное звено всегда дает
отставание по фазе на угол
.
см. ниже =>
Lm(ω)
= 20lg A(ω)
= 20lgK– 20lg
T∙ω
=> см. ниже
Найдем w(t) и h(t) =>
h(t)
= Z -1[H(s)]
= Z -1[
]
=
Z
-1[1/s2]
= (K/T) ∙t =>
h(t) = (K/T)∙t => см. ниже
т.к.
w(t)
= h’(t)
=> w(t)
=
,
где множитель 1(t) обеспечивает равенство нулю w(t) при t ≤ 0.
Примерами идеального усилительного звена можно считать: широкополосный электронный усилитель (приближенно); механический редуктор без учета инерционности и нелинейных эффектов; жесткую механическую муфту и т.д.
Примером идеального дифференцирующего звена можно считать тахогенератор =>
, где u(t)
– напряжение на клеммах тахогенератора;
φ(t) – угол
поворота якоря (ротора) тахогенератора.
Примером идеального интегрирующего звена можно считать большинство электродвигателей (без учета инерционности якоря), где входным воздействием считать напряжение в обмотке возбудителя (двигателем постоянного тока), а выходным воздействием – угол поворота выходного вала.
где E(t) – напряжение в обмотке возбуждения (или ток); φ(t) – угол поворота выходного вала электродвигателя (ЭД).