2.12. Mетод переменных состояния.
u
1
W(s)
m CAP p
Система имеет много передаточных функций: количество ТХР. Поэтому для таких многомерных систем удобно другое математическое описание.
u1(t)
x
1 (t) y1(t)
u2(t) x2(t) y2(t)
um(t) xn(t) yp(t)
Между «половинами»
существуют внутренние переменные
,
для каждой из которых можно записать
линейное ОДУ первой степени.
Обычно
.
В матричной форме эта система записывается
в виде:
,
где
- вектор столбец производных переменных
состояния;
- вектор столбец переменных состояния;
- вектор выхода;
- вектор входа (или вектор управления);
– собственная матрица системы
;
-
постоянные коэффициенты;
– матрица входа
;
- какие-то постоянные коэффициенты;
– матрица выхода
;
– матрица обхода или дополнительная
матрица выхода
;
Собственная матрица системы однозначно определяет динамические свойства системы:
-
первая система представляет собой систему ОДУ в обыкновенной форме Коши, вторая часть - система уравнений, описывающих выход. ОДУ в форме Коши подразумевают наличие начальных условий.
В нашем случае почти всегда все элементы матрицы D будут нулевыми D = 0.
Такое описание системы позволяет с одной стороны стандартным образом описывать стандартные системы, используя богатое программное обеспечение, с другой стороны для простых систем, описанных в переменных «вход-выход», переход к описанию в переменных состояния зачастую позволяет устранить технические трудности, связанные с решением ОДУ высокой степени.
Поэтому в дальнейшем мы и будем использовать подобное описание.
2.12. Переход от описания переменных «вход-выход» к переменным состояния и обратно
Рассмотрим несколько вариантов перехода. Переход зависит от правой части:
2.12.1. Правая часть содержит только b0 u(t)
Допустим, что :
Введем новую переменную х1.
Первое уравнение системы:
.
;
;
;
.
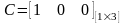2.12.2. Правая часть общего вида
Сделаем преобразования: перейдем к уравнениям динамики в изображениях:
Начальные условия нулевые.
,
(*)
где
,
- полиномы.
Разделим все уравнение (*) на полиномы :
- какая-то комплексная величина (отношение
двух комплексных величин).
Можно
считать:
,
- изображение какой-то переменной
Рассмотрим:
и преобразуем:
,
где
- какой-то дифференциальный оператор.
+
н.у.
получится задача Коши
получим
вектор переменных состояния
.
Найдем теперь регулируемую величину:
Рассмотрим:
Перейдем к оригиналам:
Пример:
u(t) y(t)
W(s)
U(s) Y(s)
н.у.
нулевые.
Необходимо свести задачу к нормальной форме Коши.
;
Разделим
левую и правую части на
Перейдем от изображений к оригиналам:
,
первое матричное уравнение:
- н.у.. Получаем задачу Коши для ОДУ.
- найдены.
Рассмотрим
:
;
.
Получили второе уравнение матричной системы:
;
;
.