2.10. Весовая и переходная функции звена (системы).

Весовой функцией звена (системы) называется реакция системы при нулевых н.у. на единичное импульсное воздействие.

 (t) Звено y (t) = W (t)

Переходной функцией звена (системы) при н.у. называется реакция на единичное ступенчатое воздействие.

1 (t) y (t) = h (t)

Звено

Весовая функция

x(t) =  (t) y(t)  w(t) x(t)

W(s) пл = 1 w(t)

t

Переходная функция

h(t)

x(t) = 1(t) y(t)  h(t) x(t)

W(s) 1

t

Учитывая, что

 (t) w(t)

W(s)

X(s) = 1 Y(s)  W(s)

Передаточная функция играет роль изображения реакции звена или системы на единичное импульсное воздействие.

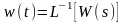- обратное преобразование Лапласа

x(t)  1(t) y(t)  h(t)

W(s)

X(s) = 1/s Y(s)  H(s)

H(s) – изображение h(t), т.е.

2.11. Определение переходного процесса в системе (сар) (звене) через весовую и переходную функции.

x(t) y(t) = ?

W(s)

X(s) Y(s) = ?

На вход системы поступает произвольное воздействие x(t) (заранее известное).

Найти: если известны и

- связь между входным и выходным воздействиями.

где х – нелинейное действие.

Символически данное соотношение записывается:

где «*» - знак свертки.

Можно решить с помощью формулы Дюамеля-Карсона:

где  - вспомогательное время интегрирования.

Если  0, то

,

Заменяя в формуле Дюамеля-Карсона верхний предел t на , получим:

Существуют стандартные подпрограммы на ЭВМ для расчета свертки.

Найдем процесс по переходной функции:

x (t) y(t) = ?

W(s)

X(s) Y(s) = ?

Запишем в изображениях связь между входом и выходом:

;

,

• формула для определения Справедлива только при нулевых н.у., когда добавка равна нулю.