4.Схематизация условий закрепления. Определение реакций опор.

Условия закрепления называют связями. Силы, с которыми действуют на связи, называют опорами. Балкой называют стержень, нагруженный силами, действующими в направлении, перпендикулярном его оси. Консольнойбалкой называют балку, которая заделана (защемлена) на одном конце и свободна на другом.

Все опорные связи условно делятся на три основных типа:

1)Подвижная шарнирная опора

Такая опора не препятствует вращению конца бруса и его перемещению вдоль плоскости качения. В ней может возникать только одна реакция , которая перпендикулярна плоскости качения и проходит через ось катка.

сила, с которой реагирует опора.

2) Неподвижная шарнирная опора

Такая опора допускает вращение конца бруса, но устраняет поступательное движение её в любом направлении. Возникающую в ней реакцию можно разложить на две составляющие, одна из которых направлена вдоль оси бруса , другая - перпендикулярно к оси бруса .

3) Жёсткая заделка

Такое закрепление не допускает ни линейных, ни угловых перемещений опорного сечения. В этой опоре в общем случае может возникать реакция, которую обычно раскладывают на две составляющие и момент защемления .

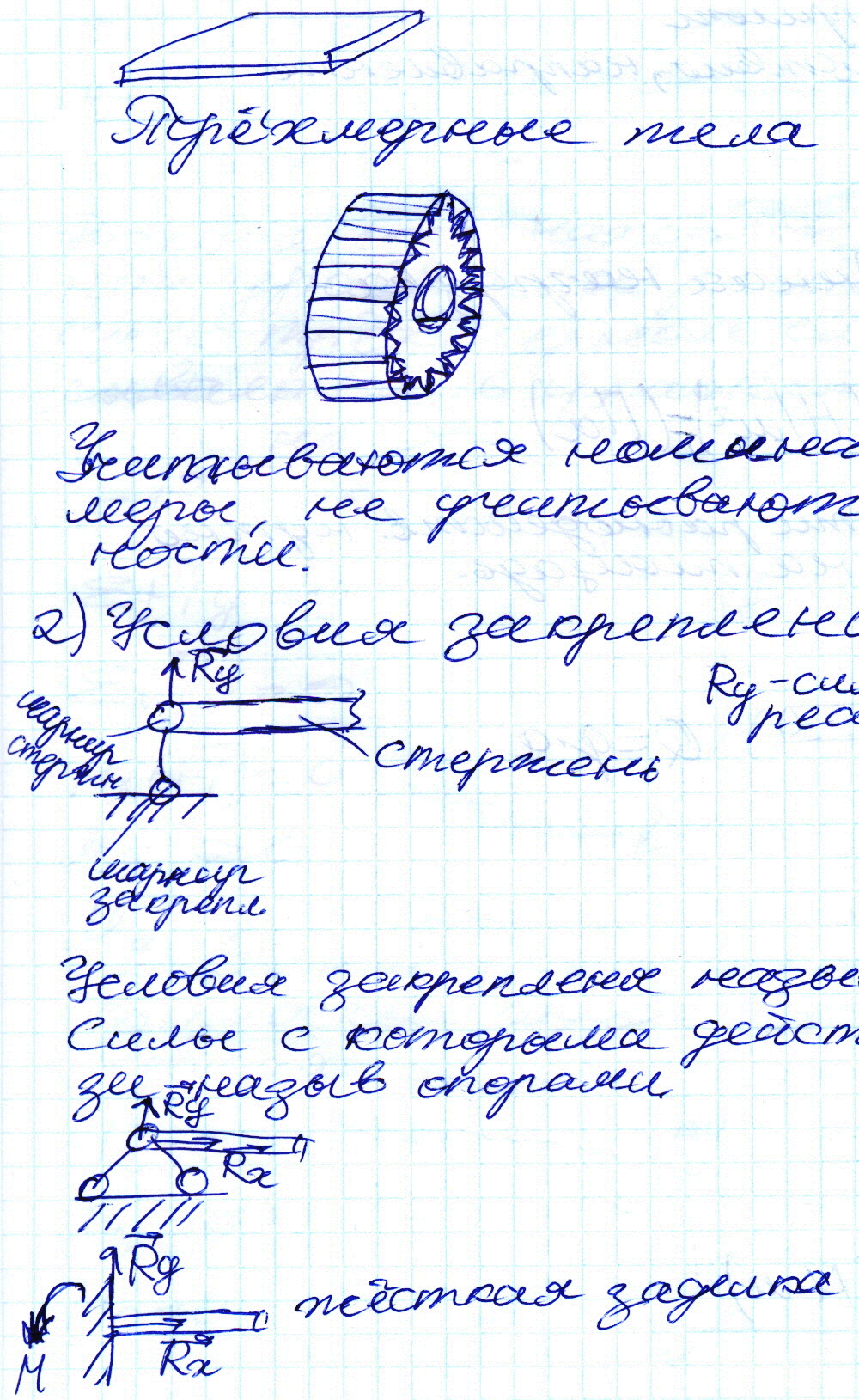
Реакции опор находятся из решения уравнения равновесия. В общем трёхмерном случае записывается 6 уравнений в проекциях на ось.

В плоском случае уравнений равновесия 3.

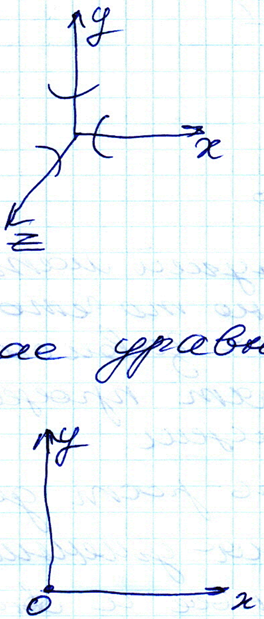
5.Напряжённое состояние в точке.

Если к телу приложена внешняя нагрузка, то внутри его возникают внутренние усилия.Интенсивность внутренних усилий называют напряжением.

Напряжение - это внутренняя сила, приходящаяся на единицу площади в данной точке данного сечения. Единица измерения – паскаль. Прочность всех материалов измеряется в миллионах , поэтому применяют:

Полное напряжение можно разложить на две составляющие:

а) нормальную к плоскости сечения, называемую нормальным напряжением ;

б) лежащую в плоскости сечения, называемую касательным напряжением .

Нормальные напряжения возникают, когда под действием внешних сил частицы, расположенные по обе стороны от сечения, стремятся удалиться одна от другой или сблизиться. Касательные напряжения возникают, когда частицы стремятся сдвинуться одна относительно другой в плоскости сечения.

Совокупность напряжений, возникающих во множестве площадок, проходящих через рассматриваемую точку, называется напряжённым состоянием в точке.

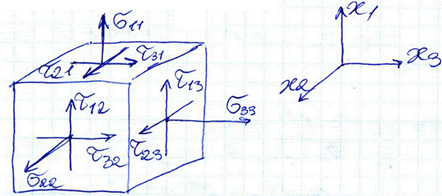
Напряжённое состояние в точке в общем случаенагружения характеризуется нормальными и касательными напряжениями, действующими на 3-х взаимно ортогональных площадках. Чтобы охарактеризовать напряженное состояние в произвольной точке тела, используя метод сечений, выделяют в её окрестности некоторый объем в виде элементарного параллелепипеда, грани которого перпендикулярны координатным осям.

Если размеры параллелепипеда уменьшать, он будет стягиваться в эту точку. В пределе все грани параллелепипеда пройдут через рассматриваемую точку и напряжения на соответствующих плоскостях параллелепипеда могут рассматриваться как напряжения в исследуемой точке.

Полное напряжение, возникающее на площадке параллелепипеда может быть разложено на три составляющие, одну по нормали к площадке и две в её плоскости.Всего на гранях параллелепипеда будет9 компонент напряжённого состояния: три нормальных и шесть касательных напряжений. Нормальные напряжения обозначают с индексами, соответствующим координатным осям. Касательные напряжения обозначают с двумя индексами. Первый индекс соответствует оси, вдоль которой направлен вектор, второй – оси, перпендикулярной площадке.Нормальное (растягивающее) напряжение, направленное от сечения, считают положительным, направленное к сечению (сжимающее) – отрицательным.

Закон парности касательных напряжений: На двух взаимно перпендикулярных площадках составляющие касательных напряжений, ортогональные их общему ребру, равны по величине и направлены оба либо к ребру, либо от него.

Напряжённое состояние в точке характеризуется 6-ю значениями напряжения, которые приводят к выбранной системе координат.