12.Работа по перемещению заряда. Работа по разным путям и замкнутым траекториям.

На положительный точечный заряд q в электрическом поле с напряжённостью E действует сила F = q E.

Работа-произведение силы и перемещения.

φ=0 A=FS;

φ=180 A= -FS

φ=90 A=0

A=FScosɑ

Рассмотрим перемещение точечного заряда q в поле точечного заряда Q, напряженность поля которого E=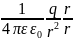

Работа, совершаемая электрическим полем при перемещении заряда q из точки 1 в точку 2, определяется следующим образом: A=q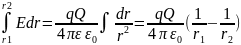

Отсюда следует, что работа сил электрического поля не зависит от формы пути, а определяется только начальным и конечным положениями заряда q.

Работа, совершаемая силами электрического поля при перемещении единичного положительного заряда по замкнутому контуру длиной l, определяется как циркуляция вектора напряженности электрического поля:

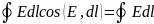
Так как для замкнутого пути положения начальной и конечной точек перемещения заряда совпадают, то работа сил электрического поля на замкнутом пути равна нулю, а значит, равна нулю и циркуляция вектора напряженности

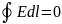
Равенство нулю означает, что силы электрического поля являются силами консервативными, а само поле - потенциальным.

13.Потенциальная энергия. Потенциальная энергия взаимодействия пары зарядов. Потенциальная энергия группы зарядов.

Потенциальная энергия заряда в электрическом поле. Работу, совершаемую силами электрического поля при перемещении положительного точечного заряда q из положения 1 в положение 2, представим как изменение потенциальной энергии этого заряда:

где Wп1 и Wп2 – потенциальные энергии заряда q в положениях 1 и 2. При малом перемещении заряда q в поле, создаваемом положительным точечным зарядом Q, изменение потенциальной энергии равно

При конечном перемещении заряда q из положения 1 в положение 2, находящиеся на расстояниях r1 и r2 от заряда Q,

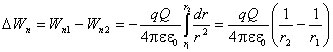
Если поле создано системой точечных зарядов Q1, Q2,¼, Qn, то изменение потенциальной энергии заряда q в этом поле:

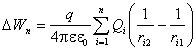
Приведённые формулы позволяют найти только изменение потенциальной энергии точечного заряда q, а не саму потенциальную энергию. Для определения потенциальной энергии необходимо условиться, в какой точке поля считать ее равной нулю. Для потенциальной энергии точечного заряда q, находящегося в электрическом поле, созданном другим точечным зарядом Q, получим

где C – произвольная постоянная. Пусть потенциальная энергия равна нулю на бесконечно большом расстоянии от заряда Q (при r ® ¥), тогда постоянная C = 0 и предыдущее выражение принимает вид

При этом потенциальная энергия определяется как работа перемещения заряда силами поля из данной точки в бесконечно удаленную. В случае электрического поля, создаваемого системой точечных зарядов, потенциальная энергия заряда q:

Потенциальная энергия системы точечных зарядов. В случае электростатического поля потенциальная энергия служит мерой взаимодействия зарядов. Пусть в пространстве существует система точечных зарядов Qi (i = 1, 2, ... , n). Энергия взаимодействия всех n зарядов определится соотношением

где rij - расстояние между соответствующими зарядами, а суммирование производится таким образом, чтобы взаимодействие между каждой парой зарядов учитывалось один раз.