11. Вычисление поля заряженной плоскости с помощью закона Гаусса.

Если заряд сосредоточен в тонком поверхностном слое несущего заряд тела, распределение заряда в пространстве можно охарактеризовать с помощью поверхностной плотности о, которая определяется выражением

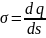
Если заряд распределен по объему или поверхности цилиндрического тела (равномерно в каждом сечении), используется линейная плотность заряда

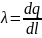
Поле бесконечной однородно заряженной плоскости.

Пусть поверхностная плотность заряда во всех точках плоскости одинакова и равна а; для определенности будем считать заряд положительным. Из соображений симметрии вытекает, что напряженность поля в любой точке имеет направление, перпендикулярное к плоскости. Действительно, поскольку плоскость бесконечна и заряжена однородно, нет никаких оснований к тому, чтобы вектор Е отклонялся в какую-либо сторону от нормали к плоскости. Далее очевидно, что в симметричных относительно плоскости точках напряженность поля одинакова по величине и противоположна по направлению. Представим себе мысленно цилиндрическую поверхность с образующими, перпендикулярными к плоскости, и основаниями величины, расположенными относительно плоскости симметрично. В силу симметрии Применим к поверхности теорему Гаусса. Поток через боковую часть поверхности будет отсутствовать, поскольку в каждой ее точке равна нулю. Для оснований совпадает с Е. Следовательно, суммарный поток через поверхность равен Внутри поверхности заключен заряд a. Согласно теореме Гаусса должно выполняться условие 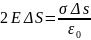из которого

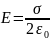
Полученный нами результат не зависит от длины цилиндра. Это означает, что на любых расстояниях от плоскости напряженность поля одинакова по величине.

Если взять плоскость конечных размеров, например заряженную тонкую пластинку то полученный выше результат будет справедливым только для точек, расстояние которых от края пластинки значительно превышает расстояние от самой пластинки.

По мере удаления от плоскости или приближения к ее краям поле будет все больше отличаться от поля бесконечной заряженной плоскости.

Поле двух разноименно заряженных плоскостей.

Поле двух параллельных бесконечных плоскостей, заряженных разноименно с одинаковой по величине постоянной поверхностной плотностью о, можно найти как суперпозицию полей, создаваемых каждой из плоскостей в отдельности. В области между плоскостями складываемые поля имеют одинаковое направление, так что результирующая напряженность равна

Вне объема, ограниченного плоскостями, складываемые поля имеют противоположные направления, так что результирующая напряженность равна нулю. Таким образом, поле оказывается сосредоточенным между плоскостями. Напряженность поля во всех точках этой области одинакова по величине и по направлению; следовательно, поле однородно. Линии напряженности представляют собой совокупность параллельных равноотстоящих прямых.

Поле бесконечного заряженного цилиндра. Пусть поле создается бесконечной цилиндрической поверхностью радиуса R, заряженной с постоянной поверхностной плотностью о. Из соображений симметрии следует, что напряженность поля в любой точке должна быть направлена вдоль радиальной прямой, перпендикулярной к оси цилиндра, а величина напряженности может зависеть только от расстояния от оси цилиндра.

Представим себе мысленно коаксиальную с заряженной поверхностью замкнутую цилиндрическую поверхность радиуса и высоты h. Следовательно, поток вектора Е через рассматриваемую поверхность равен Если внутрь поверхности попадает заряд ( — линейная плотность заряда). Применив теорему Гаусса, получим 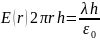отсюда

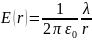
Таким образом, внутри равномерно заряженной цилиндрической поверхности бесконечной длины поле отсутствует. Напряженность поля вне поверхности определяется линейной плотностью заряда X и расстоянием от оси цилиндра. Поле отрицательно заряженного цилиндра отличается от поля цилиндра, заряженного положительно, только направлением вектора Е.

Поле, создаваемое сферической поверхностью радиуса R, заряженной с постоянной поверхностной плотностью а, будет, очевидно, центрально-симметричным. Это означает, что направление вектора Е в любой точке проходит через центр сферы, а величина напряженности является функцией расстояния от центра сферы. Вообразим концентрическую с заряженной сферой поверхность радиуса г. Для всех точек этой поверхности. Если внутрь поверхности попадает весь заряд q, распределенный по сфере. Следовательно, 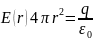откуда

Поле плоскости цилиндра

-заряд внутри цилиндра q=σs

-поток из цилиндра ES=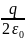

-площадь боковых граней цилиндра s=2s

-поле плоскости E=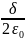

E2S= E=