Взаимное расположение прямых и плоскостей в пространстве.

Плоскости могут быть: параллельны(||), пересекаться, совпадать.

Прямые могут быть: параллельны(||), пересекаться, совпадать, скрещиваться.

Нахождение угла между плоскостями. Косинус угла между двумя плоскостями

A₁х + В₁у + C₁z + D₁ = 0 А₂х + В₂y+ C₂z + D₂ = 0,

где A₁/A₂ <>В₁/В₂<>C₁/С₂ определяется косинусом угла между нормалями п₁=(А₁;В₁;С₂) и п₂=(А₂; В₂;С₂) к этим плоскостям:

или в координатной форме:

Условие параллельности двух плоскостей (n₁||n₂):

A₁/A₂=B_l/B₂= C₁/C₂

Условие перпендикулярности двух плоскостей (n₁*n₂=0):

A₁A₂ + B_lB₂ + C₁C₂ = 0

Расстояние от точки P0(x0 ;y0;z0) до плоскости Ах + By + Cz + D = 0 вычисляем но формуле:

Нахождение расстояния между параллельными плоскостями.

Берем точку, принадлежащую одной из параллельных плоскостей, а дальше по формуле расстояния от точки до плоскости.

Пусть заданы две прямые своими каноническими уравнениями:

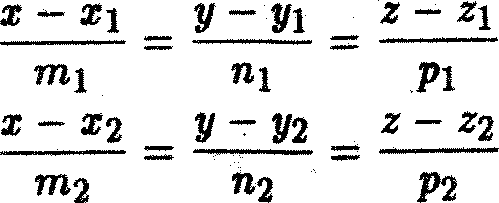
Где s₁=(m₁;n₁;p₁), s₂=(m₂;n₂;p₂) - направляющие векторы прямых, они не параллельны

(m₁/m₂<>n₁/n₂<>p₁/p₂), точки принадлежат прямым. Косинус угла между прямыми определяем по формуле. (s_1* s₂)/ (|s₁|_*|s₂|)

В координатной форме косинус угла между, прямыми опре­деляем по формуле

Условие параллельности двух прямых (s₁||s₂): m₁m₂=n₁n₂=p₁p₂

Условие перпендикулярности двух прямых: m₁m₂+n₁n₂+p₁p₂=0

Две прямые называются компланарны­ми, если они принадлежат одной плоскости или параллельным плоскостям.

Прямые компланарны, если:

1) они параллельны m₁m₂=n₁n₂=p₁p₂ или

2) пересекаются:

Если прямые скрещиваются, то выполняются условия

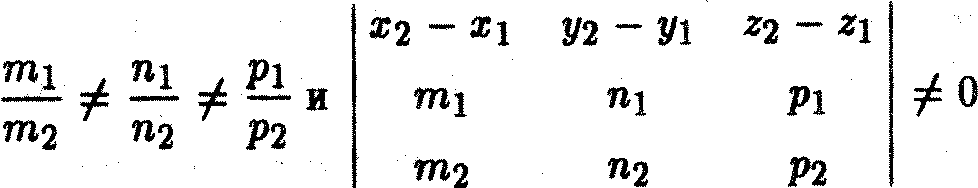
Если прямые скрещиваются, то расстояние между ними равно расстоянию между параллельными плоскостями, проведенными через заданные прямые. Вектор нормали п этих плоскостей перпен-дикулярен векторам s₁ и s₂, следовательно, n= s₁xs₂ Так как P₁(x₁;y₁;z₁), P₂(x₂;y₂;z₂) - точки, принадлежащие прямым, расстояние между скрещивающими­ся прямыми вычисляем по формуле

Пусть в пространстве заданы канонические уравнения прямой l и общее уравнение плоскости pi:

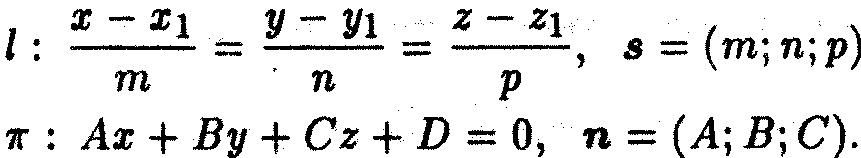
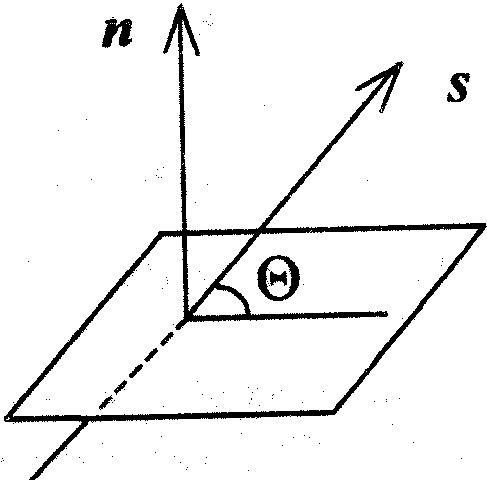
Углом между прямой и плоскостью на­зывается меньший из углов между прямой и ее проекцией на плоскость.

Синус угла между прямой и плоскостью определяем по фор­муле

В координатной форме синус угла между прямой и плоско­стью определяем по формуле

Для определения точки пересечения прямой с плос­костью решим систему уравнений плоскости и прямой, записав параметрические уравнения прямой:

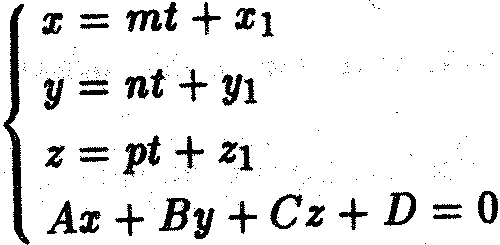
Подставим x, y, z в уравнение плоскости и найдем параметр t. Найденное значение

t = -(Ax₁+By₁+Cz₁+D)/(mA+nB+pC) подставляем в параметрическое уравнение прямой и вычисляем координаты точки пересечения. Если mA+nB+pC<>0, то прямая пересекае плоскость в единственной точке.

Условие параллельности прямой и плоскости:

mA+nB+pС=0 и Ax₁+By₁+Cz₁+D<>0

Условие ортогональности прямой и плоскости:

m/A=n/B=p/C

Условие принадлежноности прямой и плоскости:

mA+nB+pС=0 и Ax₁+By₁+Cz₁+D=0

Вычисление расстояния между параллельными прямыми:

Решение: Составим уравнение плоскости, проходящей через точкуP₁(x₁;y₁;z₁), принадлежащую первой прямой и перпендикулярной заданным прямым (n=s=(m₂;n₂;p₂):

m₂(x-x₁)+n₂(y-y₁)+p₂(z-z₁)). Записав параметрические уравнения второй прямой, найдем точку Р пересечения второй прямой и плоскости. Далее подставляя найденное значение t в параметрическое уравнение прямой, находим точку Р. Найдем вектор РР_1, и расстояние между прямыми | РР₁|.

14