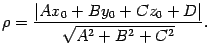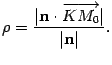Уравнение плоскости, проходящей через три различные точки, не лежащие на одной прямой:

Поставим перед собой цель – вывести уравнение плоскости, проходящей через три различные точки М₁(x₁,y₁,z₁) M₂ (x₂, y₂,z₂) M₃(x₃,y₃,z₃), не лежащие на одной прямой. Так как указанные три точки не лежат на одной прямой, векторы М₁ M₂={ x₂ - x₁, y_2- y₁, z_2- z₁} и М₁M₃=={ x₃ - x₁, y_3- y₁, z_3- z₁} не коллинеарный, а поэтому точка М(x,y,z) лежит в одной плоскости с точками М₁,M₂, M₃ , тогда и только тогда, когда векторы М₁ M₂ и М₁M₃ и М₁ M={ x - x₁, y_- y₁, z_- z₁} компланарны, т.е. тогда и только тогда, когда смешанное произведение этих трех векторов равно нулю. Использую выражение смешанного произведения в координатах, мы получим необходимое и достаточное условие принадлежности М(x,y,z) к указанной плоскости в виде:

x - x₁ y - y₁ z -z₁

x₂ - x₁ y_2- y₁ z_2- z₁ =0

x₃ - x₁ y_3- y₁ z_3- z₁

уравнение первой степени и является уравнением искомой плоскости.

Расстояние от точки до плоскости

        Пусть плоскость задана уравнением и дана точка . Тогда расстояние от точки до плоскости определяется по формуле

Доказательство.     Расстояние от точки до плоскости  -- это, по определению, длина перпендикуляра , опущенного из точки на плоскость (рис. 11.9).

В ектор и нормальный вектор n плоскости параллельны, то есть угол между ними равен 0 или , если вектор n имеет направление противоположное, указанному на рис. 11.9. Поэтому

Откуда

Координаты точки , которые нам неизвестны, обозначим . Тогда . Так как , то . Раскрыв скобки и перегруппировав слагаемые, получим

Точка лежит на плоскости , поэтому ее координаты удовлетворяют уравнению плоскости: . Отсюда находим, что . Подставив полученный результат в формулу  получим . Так как , то из формулы  следует формула 

12

Общее уравнение прямой в пространстве.

Прямая в пространстве является линия пересечения двух различных и не параллельных плоскостей, определяемых уравнениями. А₁х+В₁у+С₁z+D₁=0 и A₂x+B₂y+C₂z+D₂=0. можно задавать либо двумя уравнениями этих плоскостей, либо двумя любыми различными уравнениями пучка а(А₁х+В₁у+С₁z+D₁)+b(A₂x+B₂y+C₂z+D₂)=0.

Каноническое уравнение прямой. Оно задает точку, через которую проходит прямая и направление: х= х₀+nt

Y=y₀ +mt

Z=z₀ +lt

Параметрическое уравнение прямой следует из векторного уравнения прямой: r-r₀=ts, t пренадлежит R. То есть параметрическое уравнение: =t, t пренадлежит R

Уравнение прямой, проходящей через две заданные точки

M₁(х_1, у_1, z₁ ) и М₂(x_2, y_2,z₂)

М₁

М₂ S=M₁M₂ ={x₂ -x₁ , y₂-y₁, z₂-z₁}

S

L

Восп-ся каноническим уравнением прямой, выбираем в качестве точки М₀ в точке М а в качестве направляющего вектора S вектор M₁M₂.

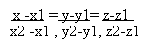
Прямая в пространстве может быть задана как линия пересечения двух плоскостей

А₁х+В₁у+С₁z+D₁=0 и A₂x+B₂y+C₂z+D₂=0 если А₁ / A₂не равно В₁ /B₂ не равно С₁ /C_2. уравнения называются общими уравнениями прямой. Чтобы привести общие уравнения прямой к каноническому виду, находим направляющий вектор s=n1*n2 где n1={A1,B1,C1} и n2{A2,B2,C2}-векторы номралей к данным плоскостям и точку принадлежащую прямой. Для этого удобно одну из переменных в системе уравнений плоскостей задать равной нулю, а две другие находим решая полученную систему.

13