Уравнение прямой, проходящей через две заданные точки

M₁(х_1, у₁ ) и М₂(x_2, y₂)

М₁

М₂ S=M₁M₂ ={x₂ -x₁ , y₂-y₁ }

S

L

Восп-ся каноническим уравнением прямой, Выбир в качестве точки М₀ в точке М а в качестве направляющего вектора S вектор M₁M₂.

Р асстояние от точки до прямой.

M₁

L M₀M₁ ={x₁ –x₀ , y₁-y₀ }

D=S(M₀ ,L)

d S пл. пар= | M₀M₁*S₁ |

d=| M₀M₁ |*S₁ |/|S|

Взаимное располодение двух прямых на плоскости:

1) перпендикулярно; 2) параллельно.

Угол между двумя прямыми определяется как угол между их направляющими векторами

L= ;M1(x1,y1); S={n, m}; N= ;R={p,q }; M2(x2,y2); SR=|S|*|R|*cos(f)=n*p+m*q _; Cos(f)=

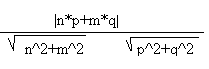
Условие параллельности двух прямых.

L|| N тогда и только тогда, когда S || R тогда и только тогда, когда

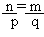
Условие перпендикулярности двух прямых,

L N тогда и только тогда, когда S R тогда и только тогда, когда =0

11

Любая прямая, перпендикулярная плоскости, называется нормалью к плоскости, а любой ненулевой вектор на такой прямой мы будем называть нормальным вектором плоскости.         

        Замечание Из определения видно, что нормальный вектор у фиксированной плоскости определяется не однозначно. Все нормальные векторы одной плоскости коллинеарны друг другу и поэтому получаются один из другого умножением на число, отличное от нуля.         

Для того чтобы из параллельных плоскостей выбрать одну, достаточно задать точку, через которую проходит эта плоскость. Итак, если у плоскости известны нормальный вектор и точка, через которую она проходит, то плоскость определена однозначно.

        Теорема 1 Пусть вектор является нормальным вектором плоскости , проходящей через точку . Тогда уравнение

является уравнением плоскости .

         Доказательство.     Пусть  - некоторая точка плоскости (рис. 11.1). Иногда говорят "текущая точка" плоскости, так как предполагается, что ее координаты меняются и точка пробегает всю плоскость.

Вектор лежит на плоскости . Следовательно, вектор ортогонален вектору n. Если же взять точку Q, не лежащую на плоскости , то вектор не будет ортогональным вектору n. Так как условием ортогональности двух векторов является равенство нулю их скалярного произведения, то условием того, что точка лежит в плоскости , является выполнение равенства

Выразив скалярное произведение в левой части этого равенства через координаты сомножителей по формуле 

получим формулу 

Пусть r -- радиус-вектор текущей точки плоскости ,  - радиус-вектор точки . Тогда уравнение  можно переписать в виде

Такое уравнение обычно называют векторным уравнением плоскости .

Раскроем скобки в уравнении  Так как точка  - фиксированная, то выражение является числом, которое обозначим буквой . Тогда уравнение  принимает вид

Такое уравнение называется общим уравнением плоскости. Еще раз отметим, что в этом уравнении хотя бы один из коэффициентов отличен от нуля, так как .

Верно и обратное утверждение:

        Теорема 2 Всякое уравнение ( ), в котором , является уравнением плоскости, ортогональной вектору .

        Доказательство.     Условие означает, что хотя бы одно из чисел , отлично от нуля. Пусть это будет, например, число . Преобразуем уравнение  следующим образом:

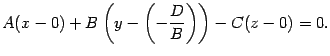
По теореме 1 такое уравнение является уравнением плоскости с нормальным вектором n, проходящей через точку .     

Рассмотрим теперь полное уравнение плоскости и покажем, что оно может быть приведено к следующему виду. , называемому уравнением плоскости «в отрезках». Так как коэффициенты А В С D отличны от нуля то мы можем переписать уравнение в виду и затем положить a=-D/A, b=-D/B, c=-D/C. В уравнении плоскости в отрезках числа a, b и c имеют простой геометрический смысл: они равны величинам отрезков, которые отсекает плоскость на осях Ох, Оу и Oz соответственно (отрезки отсчитываются от начала координат). Чтобы убедиться в этом, достаточно найти точки пересечения плоскости, определяемой уравнением плоскости в отрезках с уравнениями у=0 и z=0 оси Ох. Мы получим координаты точки пересечения х=а, y=0, z=0. Аналогично устанавливается, что координаты точки пересечения плоскости с осью Оу равны х=0, y=b, z=0 и с осью Oz равны х=0, y=b, z=с.