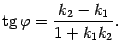Уравнение прямой с угловым коэффициентом.

Пусть заданы две прямые и , ( ). Тогда, если , то угол между этими прямыми можно найти из формулы

Если , то прямые перпендикулярны.

        Доказательство.     Как известно из школьного курса математики, угловой коэффициент в уравнении прямой равен тангенсу угла наклона прямой к оси . Из рис. 11.10 видно, что .

Т ак как , , то при выполняется равенство

что дает формулу 

Если же , то , откуда

Следовательно, и .    

Общее уравнение прямой.

Докажем сначала, что если на плоскости П задана произвольная прямая линия L и фиксированная произвольная декартова прямоугольная систему Оху, то прямая L определяется в этой системе уравнением первой степени.

Достаточно доказать, что прямая L определяется уравнением первой степени при каком-то одном специальном выборе декартовой прямоугольной системы на плоскости П, ибо тогда она будет определяться уравнением первой степени и при любом выборе декартовой прямоугольной системы на плоскости П . Направим ось Ох вдоль прямой L, а ось Оу перпендикулярно к ней. Тогда уравнением прямой будет уравнение первой степени у=0. в самом деле, этому уравнению будут удовлетворять координаты любой точки, лежащей на прямой L, и не будут удовлетворять координаты ни одной точки, не лежащей на прямой L.

Докажем теперь, что если на плоскости П фиксирована произвольная декартова система Оху, то всякое уравнение первой степени с двумя переменными х и у определяет относительно этой системы прямую линию.

В самом деле пусть фиксирована произвольная декартова прямоугольная системы Оху и задано уравнение первой степени Ах+Ву+с=0, в котором А В С- какие угодно постоянные, причем из постоянных А и В хотя бы одна отлична от 0. уравнение заведомо имеет хотя бы одно решение х0 и у0, т.е. существует хотя бы одна точка М(х_0, у₀) координаты которой удовлетворяют уравнению Ах₀+Ву₀+С=0_. вычитая из уравнения первой степени уравнение где подставлена точка М(х_0, у₀), мы получим уравнение: А(х- х₀)+В(у- у₀)=0₍₁₎, эквивалентное уравнении первой степени. Достаточно доказать, что уравнение определяет относительно системы некоторую прямую. Мы докажем, что уравнение ₍₁₎ определяет прямую L, проходящую через точку М(х_0, у₀) и перпендикулярную вектору n={A,B}. В самом деле, если точка М(х,у) лежит на указанной прямой L, то ее координаты удовлетворяют уравнению (1), ибо в этом случае векторы n={A,B} и М₀М={x-x_0,у-у₀} ортогональныи их скалярное произведение А(х- х₀)+В(у- у₀) равно нулю. Если же точка М(х,у) не лежит на указанной прямой, то ее координаты не удовлетворяют уравнению (1), ибо в этом случае векторы n={A,B} и М₀М={x-x_0,у-у₀} не ортогональны и поэтому их скалярное произведение не равно нулю. Утверждение доказано

Уравнение Ах+Ву+С=0 с произвольными коэффициентами А В иС такими, что А и В не равны нулю одновременно, называется общим уравнением прямой. Мы доказали, что прямая определяемая общим уравнением Ах+Ву+С=0 ортогональна к вектору n={A,B}. Этот последний вектор мы будем называть нормальным вектором прямой.

Каноническое уравнение прямой. Любой ненулевой вектор, параллельный данной прямой, будем называть направляющим вектором этой прямой. Поставим перед собой задачу: найти уравнение прямой, проходящей через данную точку М₁(х₁,у₁) и имеющей заданный направляющий вектор q={l,m}. Очевидно точка М(х,у) лежит на указанной прямой тогда и только тогда, когда векторы М₁М={x-x_1, y-y₁} и q={m,l} коллинеарны, тогда и только тогда, когда координаты этих векторов пропорциональны, т.е.

Рассмотрим теперь полное уравнение плоскости и покажем, что оно может быть приведено к следующему виду. , называемому уравнением плоскости «в отрезках». Так как коэффициенты А В С отличны от нуля то мы можем переписать уравнение в виду и затем положить А=-С/А b=-C/B. В уравнении плоскости в отрезках числа a, b имеют простой геометрический смысл: они равны величинам отрезков, которые отсекает плоскость на осях Ох, Оу соответственно (отрезки отсчитываются от начала координат). Чтобы убедиться в этом, достаточно найти точки пересечения прямой, определяемой уравнением прямой в отрезках с осями координат. Например точка пересечения с осью Ох определяется из совместного рассмотрения уравнения прямой в отрезках с уравнением у=0 оси Ох. Мы получим координаты точки пересечения х=а у=0. Аналогично устанавливается, что координаты точки пересечения прямой с осью Оу имеют вид х=0 и у=b.