Cвойства смешанного произведения:

1. a(b) = (ab);

2. a(b₁+b₂)c = ab₁c + ab₂c.

        Доказательство.     Соотношения a(b) = (ab) и a(b₁+b₂)c = ab₁c + ab₂c следуют из того, что abc является скалярным произведением а на bc и из линейности скалярного произведения.

Для второго аргумента: в силу равенства *  выполнено abc=bca, поэтому

a(b)c = (b)ca = (bca) = (abc),

a(b₁+b₂)c = (b₁+b₂)ca= b₁ca+b₂ca= ab₁c+ab₂c

Для третьего аргумента свойство линейности доказывается аналогично.

Смешанное произведение векторов равно нулю тогда и только тогда, когда сомножители a,b,c компланарны.

        Доказательство.     По определению abc=a(bc). В силу свойства скалярного произведения abc=0 тогда и только тогда, когда векторы a и bc ортогональны. Если bc0, то вектор bc ортогонален плоскости векторов b,c, и, следовательно, a лежит в плоскости векторов b,c. Если bc=0 , то векторы b и c коллинеарны, но тогда векторы a,b,c компланарны.     

Смешанное произведение в ортонормированном базисе:

abc = a(b x c)

1. i j k

b x c = x₂ y₂ z₂ = i(y₂z3 – y₃z₂) – j(x₂z₃ – x₃z₂) + k(x₂y₃ – x₃y₂)

x₃ y₃ z₃

2. a(b x c) = x₁(y₂z3 – y₃z₂) – y₁(x₂z₃ – x₃z₂) + z₁(x₂y₃ – x₃y₂) т.е.:

x₁ y₁ z₁

3. a(b x c) = x₂ y₂ z₂

x₃ y₃ z₃

8

Подмножество H линейного пространства L называют линейным подпространством, если выполнены следующие условия:

1. Cумма любых двух векторов из H принадлежит H

2. Произведение любого вектора из H на любое действительное число снова принадлежит H

Фактически говорят о том, что линейное подпространство-это любое подмножество данного линейного пространства, замкнутое относительно линейных операций, т.е. применение линейных операций к векторам, принадлежащим этому подмножеству не выводит результат за пределы подмножества.

В любом линейном пространстве L всегда имеются два линейных подпространства: само линейное пространство L и нулевое подпространство {0},состоящее из единственного элемента 0.Эти линейные подпространства называют несобственными, в то время как все остальные линейные подпространства называют собственными.

Пусть в линейном пространстве L задана система векторов e1,e2,…..ek.Рассмотрим множество H всех векторов в L,которые могут быть представлены линейной комбинацией этих векторов. Это множество является линейным подпространством в L.Действительно пусть x=x1e1+…Xkek , y=y1e1+…+ykek ,тогда x+y=(x1+y1)e1+…+(xk+yk)ek э H

ax=(ax)e1+…+(axk)ek, где a-действительное число. Описанное линейное подпространство называют линейной оболочкой системы векторов e1,e2,…,ek и обозначают span{e1,e2,…,ek}.

Базис и размерность подпространства

Линейное подпространство является линейное пространством относительно операций объемлющего линейного пространства и поэтому имеет размерность и базис.

Th1:Если H-линейное подпространство линейного пространства L, то dimH<=dimL,

Если к тому же H<>L то dimH<dimL

Th2:Если H1и H2 линейное подпространство линейного пространства L, то dim(H1+H2)=dimH1+dimH2-dim(H1/\H2)

9

Д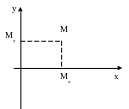 ве перпендикулярные оси на плоскости с общим началом и одинаковой масштабной единицей образуют декартову прямоугольную систему координат на плоскости

Одну из указанных осей называют осью Ox (абсцисс), а

другую осью Oy (ординат).

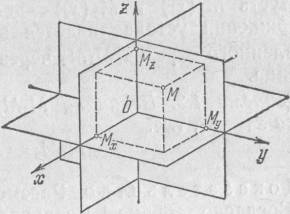
Декартовы координаты в пространстве вводятся в полной аналогии с декартовыми координатами на плоскости. Три взаимно перпендикулярных оси в пространстве (координатные оси) с общим началом О и одинаковой масштабной единицей образуют декартову прямоугольную систему координат в пространстве. Одну из указанных осей называют осью ox или осью абсцисс, другую осью oy или осью ординат, а третью – осью oz или осью аппликат.

Координаты – числа, заданием которых определяется положение точки на прямой, на плоскости или в пространстве (соответственно на линии или поверхности).

Уравнение Ф(x,y) называется уравнением линии L (относительно заданной системы координат), если этому уравнению удовлетворяют координаты x и y любой точки, лежащей на линии L, и не удовлетворяют координаты x и y ни одной точки, не лежащей на линии L. С точки зрения этого определения сама линия L представляет собой геометрическое место точек, координаты которых удовлетворяют уравнению Ф(x,y). Если (в заданной системе координат) рассматриваемое уравнение вида Ф(x,y) является уравнением линии L, то мы будем говорить, что это уравнение определяет линию L.

Параметрическое представление линии.

Для аналитического представления линии L часто бывает удобно выражать переменные координаты x и y точек этой линии при помощи третьей вспомогательной переменной (или параметра) t:

x=(t) , y=(t)

где функции (t) и (t) предполагаются непрерывными по параметру t (в некоторой области {t} изменения этого параметра).

Параметрическое представление линии на плоскости естественно возникает, если эту линию рассматривать как путь, пройденный материальной точкой, непрерывно движущейся по определенному закону. В самом деле, если переменная t представляет собой время, отсчитываемое от некоторого начального момента, то задание закона движения и представляет собой задание координат x и y движущейся точки как некоторых непрерывных функций x=(t) и y=(t) времени t.

Ф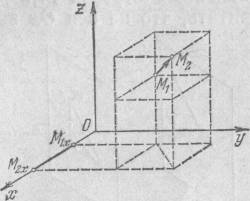 ормула для вычисления расстояния между двумя точками по известным координатам точек.

Рассмотрим в пространстве декартову систему координат Oxyz и точки M₁(x₁;y₁;z₁) и M₂(x₂;y₂;z₂). Очевидно, расстояние (M₁,M₂) между точками M₁ и M₂ равно длине направленного отрезка M₁M₂, равно длине диагонали параллелепипеда, грани которого параллельны координатным плоскостям и проходят через точки M₁ и M₂. Длина параллельного оси Ox ребра этого параллелепипеда равна, очевидно, абсолютной величине проекции отрезка M₁M₂ на ось Ox, т.е. равна |x₂-x₁|. По аналогичным соображениям длины ребер, параллельных осям Oy и Oz, равны соответственно |y₂-y₁| и |z₂-z₁|. Используя теорему Пифагора, получим следующую формулу для (M₁,M₂):

(M₁,M₂)=(( x₂-x₁)²+( y₂-y₁)²+( z₂-z₁)²)^1/2

Замечание. Формула расстояния между двумя точками в случае их расположения в плоскости Oxy имеет следующий вид:

(M₁,M₂)=(( x₂-x₁)²+( y₂-y₁)²)^1/2

Деление отрезка в заданном соотношении.

Р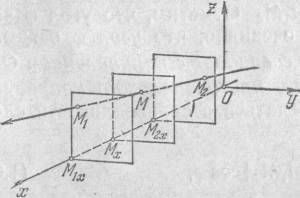 ассмотрим в пространстве две различные точки M₁ и M₂ и прямую, определяемую этими точками. Выберем на этой прямой некоторое направление. На полученной оси точки M₁ и M₂ определяют направленный отрезок M₁M₂. Пусть M – любая, отличная от M₂ точка указанной оси. Число

=M₁M/MM₂ (*)

называется отношением, в котором точка M делит направленный отрезок M₁M_2. Таким образом, любая, отличная от M₂ точка M делит отрезок M₁M₂ в некотором отношении , где  определяется равенством (*).

10