Критерий зависимости 2ух векторов:

Необходимым и достаточным условием линейной зависимости двух векторов является их коллинеарность.

Док-во: 1) необходимость. Пусть два вектора а и b линейно зависимы. Докажем коллинеарность этих векторов. По определению линейной зависимости найдутся такие вещественные числа и , хотя бы одно из которых отлично от нуля, что справедливо равенство . Пусть ради определенности, отлично от нуля число . Тогда из равенства (посредством деления этого равенства на и переброски одного члена в правую часть) получим следующее равенство: . Вводя обозначение , получим . Таким образом, вектор b равен произведению вектора a на вещественное число . По определению произведения вектора на число векторы a и b коллинеарны. Необходимость доказана.

2) Достаточность. Пусть векторы a и b коллинеарны. Докажем, что эти векторы линейно зависимы. Если хотя бы один из векторов a и b ненулевой, то эти векторы линейно зависимы в силу теоремы (если хотя бы один из векторов является ненулевым, то эти векторы являются линейно зависимыми). Таким образом, нам нужно рассмотреть лишь случай, когда векторы a и b ненулевые. Но если вектор a ненулевой, то из коллинеарности векторов a и b в силу теоремы (если вектор b коллинеарен ненулевому вектору a, то существует вещественное число такое, что ) вытекает существование такого вещественного числа , что , или, что то же самое, . Так как из двух чисел , -1 одно заведомо отлично от нуля, то равенство ( ) доказывает линейную зависимость векторов a и b. Достаточность доказана.

Критерий зависимости 3ех векторов:

Три вектора линейно зависимы тогда и только тогда, когда они компланарны.

Доказательство: Пусть три вектора линейно зависимы, т.е. , где, например, λ₃ ≠ 0. Тогда .

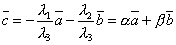Отнесём векторы и к одному началу и проведём через них плоскость. Тогда и будут лежать в той же плоскости, а потому и их сумма, т.е. будет лежать в той же плоскости, т.е. – компланарны.

Пусть теперь векторы – компланарны. Тогда они будут лежать в одной плоскости. Отнесём все три вектора к одному началу.

Если векторы и не коллинеарны, то очевидно, вектор можно предствить в виде . Действительно из рисунка видно, что , где и , а значит найдутся числа и такие, что .

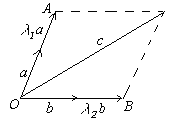Если же вектор коллинеарен вектору , то один из них линейно выражен через другой, т.е. . Что и требовалось доказать.

Таким образом, три некомпланарных вектора всегда линейно независимы. Кроме того, можно показать, что каждые четыре вектора линейно зависимы.

Линейная зависимость 4ех векторов:

Любые четыре вектора линейно зависимы.

Док-во: Прежде всего исключим случай, когда какая-нибудь тройка из указанных четырех векторов компланарна. Тогда в силу теоремы (необходимым и достаточным условием линейной зависимости трех векторов является их компланарность) указанная тройка векторов линейно зависима, а стало быть в силу теоремы (если среди n векторов какие-либо (n-1) векторов линейно зависимы, то и все n векторов линейно зависимы), и все четыре вектора линейно зависимы. 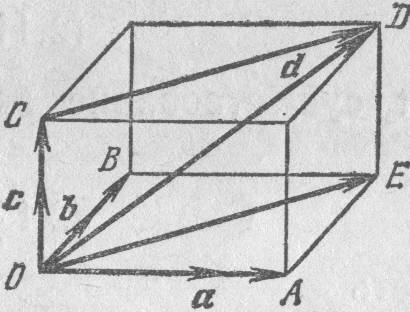Остается рассмотреть случай, когда среди четырех векторов a,b,c,d никакая тройка векторов не компланарна (и, стало быть, нет ни одной пары коллинеарных векторов и ни одного нулевого вектора( согласно следствию в тройке некомпланарных векторов не может содержаться ни одной пары коллинеарных векторов и ни одного нулевого вектора)). Приведем все 4 вектора a,b,c,d к общему началу О и проведем через конец D вектора d плоскости, параллельные плоскостям, определяемым парами векторов bc,ac,ab (векторы, входящие в каждую из указанных трех пар, не коллинеарны, а поэтому каждая из указанных трех пар определяет некоторую плоскость).Точки пересечения указанных плоскостей с прямыми, на которых лежат векторы a,b,c, обозначим соответственно буквами A,B,C (существование указанных точек пересечения вытекает из того, что векторы a,b,c не компланарны). Убедимся в том, что вектор равен сумме трех векторов , т.е. (2.14). В самом деле из правила параллелограмма сложения векторов и из параллелограмма OCDE вытекает, что , а из параллелограмма OBEA вытекает, что . Тем самым равенство (2.14) установлено. Так как вектор коллинеарен ненулевому вектору а (с которым он лежит на одной прямой), то в силу теоремы (если вектор b коллинеарен ненулевому вектору a, то существует вещественное число такое, что ) найдется такое , что . Из аналогичных соображений вытекает существование вещественных чисел и таких, что . Его можно переписать следующим образом: Так как из четырех чисел одно заведомо отлично от нуля, то последнее равенство доказывает линейную зависимость векторов a,b,c,d. Теорема доказана.

4

Определение 1. ТРИ линейно независимых вектора a, b и c образуют в пространстве базис, если любой вектор d может быть представлен в виде некоторой линейной комбинации векторов a, b и c: ( - вещественные числа, при которых справедливо равенство, их называют координатами вектора d относительно базиса a, b, c).

Определение 2 (базис на плоскости ). ДВА лежащих в плоскости линейно независимых вектора a и b образуют на этой плоскости базис, если любой лежащий в плоскости вектор с может быть представлен в виде некоторой линейной комбинации векторов a и b: .

Фундаментальные утверждения:

1. Любая тройка некомпланарных векторов a, b и c образует базис в пространстве;

2. Любая пара лежащих в данной плоскости неколлинеарных векторов a и b образует базис на этой плоскости.

Теорема о единственности разложения вектора по базису:

Каждый вектор d может быть единственным образом разложен по базису a, b, c, или (что то же самое) координаты каждого вектора d относительно базиса a, b, c определяются однозначно.

Док-во. Допустим, что для некоторого вектора d, наряду с разложением , справедливо другое разложение по тому же самому базису: .

Почленное вычитание равенств приводит к соотношению В силу линейной независимости базисных векторов a, b, c данное соотношение приводит к равенствам или . Единственность разложения по базису доказана.

Теорема.(линейные операции над векторами в координатной форме.) При сложении двух векторов и их координаты (относительно любого базиса a, b, c) складываются. При умножении вектора на любое число все его координаты умножаются на это число.

Д ок-во. Пусть . Тогда в силу свойств линейных операций над векторами:

В силу единственности разложения по базису теорема доказана.

Ортонормированный канонический базис i, j, k.

В случае декартовой прямоугольной системы координат базисные векторы принято обозначать i, j, k. Каждый из векторов i, j, k имеет длину, равную единице, причем эти три вектора взаимно ортогональны (обычно направления векторов i, j, k берут совпадающими с направлениями декартовых осей Ox, Oy, Oz соответственно). Каждый вектор d может быть, и притом единственным способом, разложен разложен по декартову прямоугольному базису i, j, k, т.е. для каждого вектора d найдется, и притом единственная тройка чисел X, Y, Z такая, что справедливо равенство . Числа X, Y, Z называются декартовыми прямоугольными координатами вектора d. (d={ X, Y, Z})

5

Скалярным произведением двух ненулевых векторов и называют число, равное произведению их длин на косинус угла между ними: .

Э ту формулу можно записать в другом виде:

Механический смысл скалярного произведения заключается в следующем: если - вектор силы, - вектор пути, то А= - работа, совершаемая силой по перемещению материальной точки из начала вектора в его конец.

Свойства скалярного произведения.

1. Переместительное:

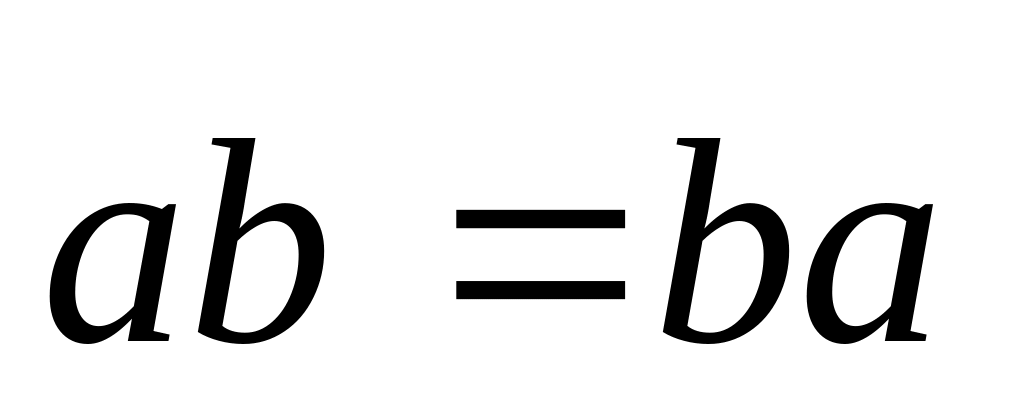
Д-во. , а . И так как , как произведение чисел и , то .

2. Сочетательное:

Д-во. .

3. Распределительное:

Д-во. .

4. Скалярный квадрат вектора=квадрату его длины:

Д-во.

Теорема. (Признак перпендикулярности (ортогональности) векторов)

Необходимым и достаточным условием ортогональности (перпендикулярности) двух ненулевых векторов является равенство нулю их скалярного произведения: (a, b) =0 <=> a ортогонален b.

Док-во.1) Необходимость. Пусть векторы a и b ортогональны, - угол между ними. Тогда =0 и в силу формулы (*) скалярное произведение ab равно нулю.

2) Достаточность. Пусть скалярное произведение ab равно нулю. Докажем, что векторы a и b ортогональны. Прежде всего исключим тривиальный случай, когда один из векторов является нулевым (он имеет неопределённое направление, и его можно считать ортогональным любому вектору). Если же оба вектора a и b ненулевые, то |a|>0 и |b|>0, и поэтому из равенства ab=0 из формулы (*) вытекает, что cos =0, т.е. векторы a и b ортогональны. Ч.т.д.

Выражение скалярного произведения через координаты.

Пусть заданы два вектора и . Учитывая, что базисные векторы являются попарно ортогональными и имеют единичную длину, получаем:

ii=1, ij=0, ki=0

ij=0, jj=1, kj=0

ik=0, jk=0, kk=1

Найдём скалярное произведение векторов, перемножая их как многочлены:

+

= , т.е.

- скалярное произведение векторов равно сумме произведений их одноименных координат.

Отсюда следствие: Необходимым и достаточным условием ортогональности векторов и является равенство .

Длина вектора.

Так как , то из   вытекает, что если , то (это также выводится из формулы нахождения диагонали прямоугольного параллелепипеда со сторонами ).

Косинус угла между векторами.

Угол между векторами и определяется по формуле = .

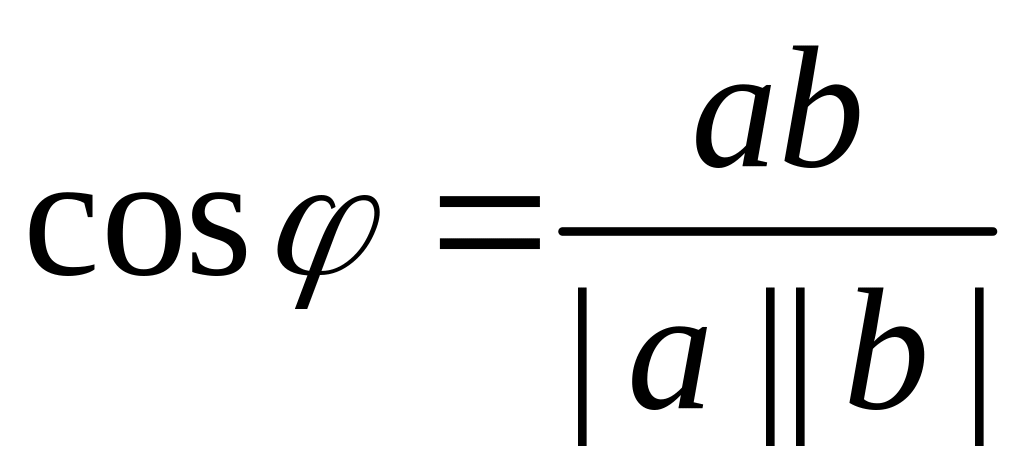Ортогональная проекция векторов a и b:

Проекция вектора b на ось, определяемую вектором a: . Следовательно подставляя формулы для модуля и косинуса получаем: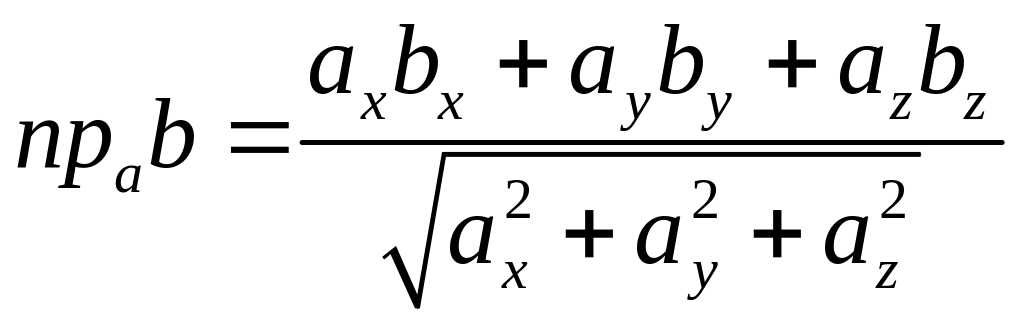 . Аналогично вычисляется .

Теорема. Декартовы прямоугольные координаты X,Y и Z вектора d равны проекциям этого вектора на оси Ox, Oy и Oz соответственно.

Д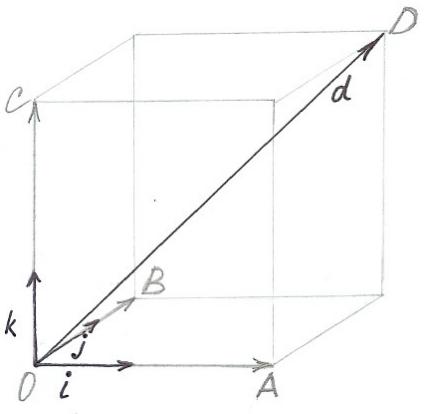 ок-во. Приложим вектор d к началу О декартовой системы и проведем через конец D этого вектора три плоскости, параллельные координатным плоскостям Oyz, Oxz и Oxy. Точки пересечения указанных плоскостей с осями Ox, Oy и Oz соответственно обозначим буквами A, B и C. Получаем, что .

, , . В рассматриваемом случае декартовой прямоугольной системы параллелепипед, построенный на базисных векторах i, j, k и имеющий вектор d своей диагональю, является прямоугольным. Поэтому проекции вектора d на оси Ox, Oy и Oz соответственно равны величинам OA, OB и OC. Для доказательства теоремы осталось убедиться в том, что OA=X, OB=Y, OC=Z.

Убедимся, например, в равенстве OA=X . В силу OA=Xi. Отсюда и из того, что i – единичный вектор, вытекает, что |OA|=|X|. Но знаки чисел OA и X совпадают, ибо в случае, когда векторы и i направлены в одну сторону, оба числа OA и X, а в случае, когда векторы и i направлены в противоположные стороны, оба числа OA и X отрицательны. Итак, OA=X. Аналогично доказываются равенства OB=Y, OC=Z. Теорема доказана.

Косинусы углов, образованных вектором с осями координат, называются направляющими косинусами вектора.

Координаты вектора равны его направляющим косинусам, умноженным на длину вектора. X=|d|cos , Y=|d|cos , Z=|d|cos . (как проекции на координатные оси).

Следовательно т.к. , тогда направляющие косинусы вектора d равны:

, , .

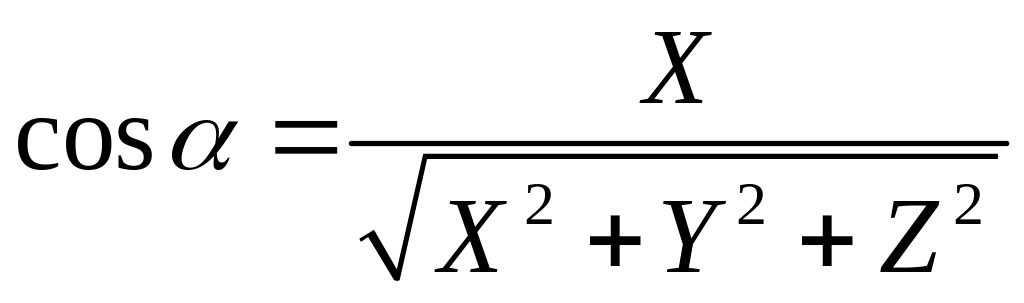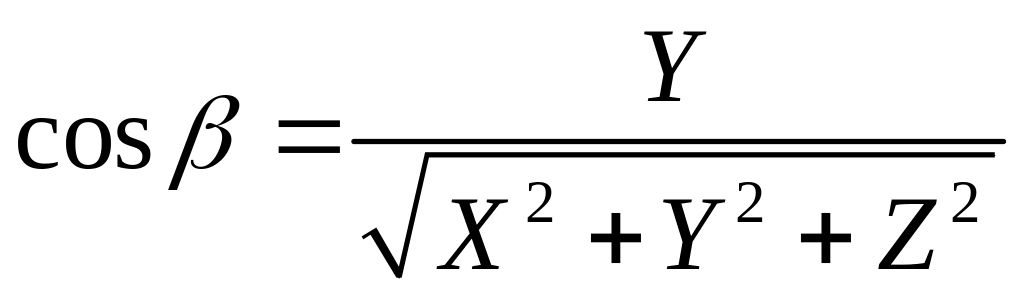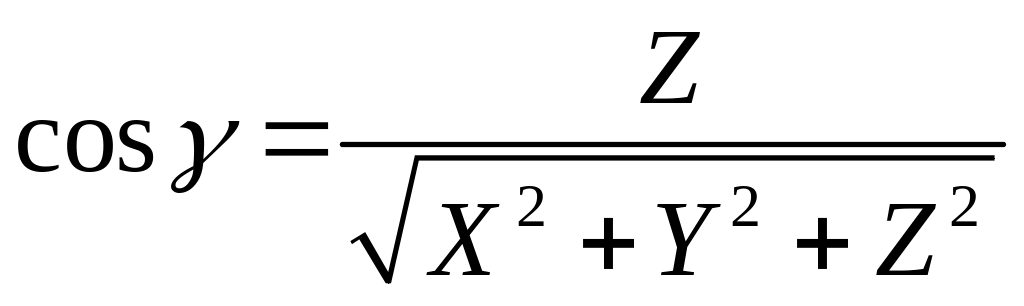Возводя в квадрат и складывая равенства, получим, что , т.е. сумма квадратов направляющих косинусов любого вектора равна единице.

6

Определение 1. Три вектора называются упорядоченной тройкой (или просто тройкой), если указано, какой из этих векторов является первым, какой-вторым, какой-третьим.

Определение 2. Тройка некомпланарных векторов abc называется правой (левой), если выполнено одно из следующих трёх условий:

1. если, будучи приведены к общему началу, эти векторы располагаются так, как могут быть расположены соответственно большой, несогнутый указательный и средний пальцы правой (левой) руки;

2. если после приведения к общему началу вектор c располагается по ту сторону от плоскости, определяемой векторами a и b, откуда кратчайший поворот от a к b, кажется совершающимся против часовой стрелки (по часовой стрелке);

3. если, находясь внутри телесного угла, образованного приведёнными к общему началу векторами a, b, c, мы видим поворот от a к b и от него к c совершающимся против часовой стрелки (по часовой стрелке).

Определение 3. Декартова система координат называется правой (левой), если три базисных вектора образуют правую (левую) тройку. (Для определённости рассматривают правые тройки координат).

Определение. Векторным произведением вектора a на вектор b называется вектор c, обозначаемый символом c=[ab] и удовлетворяющим трем следующим требованиям:

1. длина вектора с равна произведению длин векторов a и b на синус угла между ними, т.е. ;

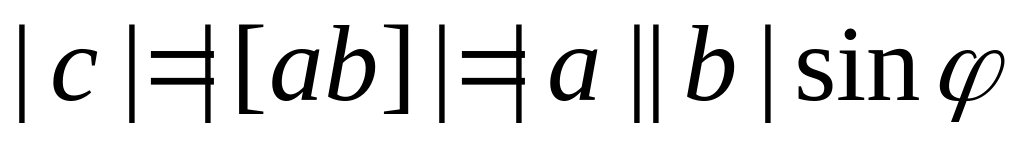2. вектор с ортогонален к каждому из векторов a и b;

3. вектор с направлен так, что тройка векторов abc является правой.

Геометрический смысл. Длина (модуль) векторного произведения [ab] равняется площади S параллелограмма, построенного на приведённых к общему началу векторах a и b. (это непосредственно вытекает из формулы )

Свойства векторного произведения.

1. Антипереместительное. При перестановке сомножителей векторное произведение меняет знак, т.е.

Д-во. Векторы и коллинеарны, имеют одинаковые модули (площадь параллелограмма остается неизменной), но противоположно направлены (тройки , , и , , противоположной ориентации). Стало быть, .

2. Сочетательное относительно скалярного множителя:

Д-во. Пусть >0. Вектор перпендикулярен векторам и . Вектор также перпендикулярен векторам и (векторы , лежат в одной плоскости). Значит, векторы и коллинеарны. Очевидно, что и направления их совпадают. Имеют одинаковую длину: | |= | |= и . Поэтому = . Аналогично доказывается при <0.

3. Распределительное (дистрибутивности): . (Без док-ва).

Теорема (признак коллинеарности векторов).

Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их векторного произведения.

Д-во: 1) Необходимость вытекает из определения вект. произведения: для коллинеарных векторов a и b векторное произведение по определению равно нулю (sin=0).

2) Достаточность. Пусть векторное призведение [ab] равно нулю. Докажем, что векторы a и b коллинеарны. Прежде всего исключим тривиальный случай, когда один из векторов является нулевым. Если же оба вектора a и b ненулевые, то |a|>0, |b|>0, и поэтому из равенства [ab]=0 и из формулы вытекает, что sin =0, т.е. векторы коллинеарны. Ч.т.д.

Вычисление векторного произведения в базисе i, j, k.

Пусть заданы два вектора: и .

Составим из тройки базисных векторов i, j, k все возможные пары и для каждой из пар подсчитаем вект. произведение. Учитывая, что базисные векторы взаимно ортогональны, образуют правую тройку и имеют единичную длину, получим( ):

[ii]=0, [ji]=-k, [ki]=j

[ij]=k, [jj]=0, [kj]=-i

[ik]=-j, [jk]=i, [kk]=0

Найдем вект. произведение векторов, перемножая их как многочлены:

=

= =

=

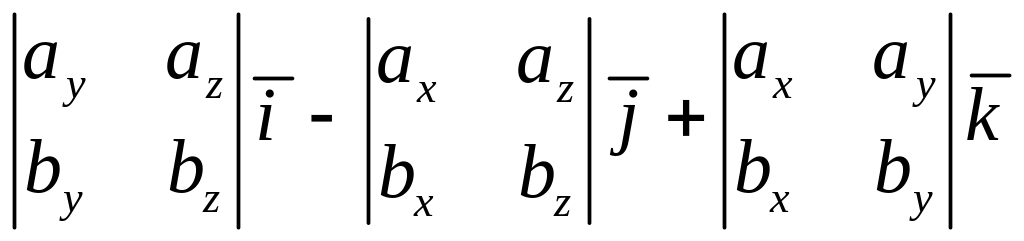= . ИЛИ

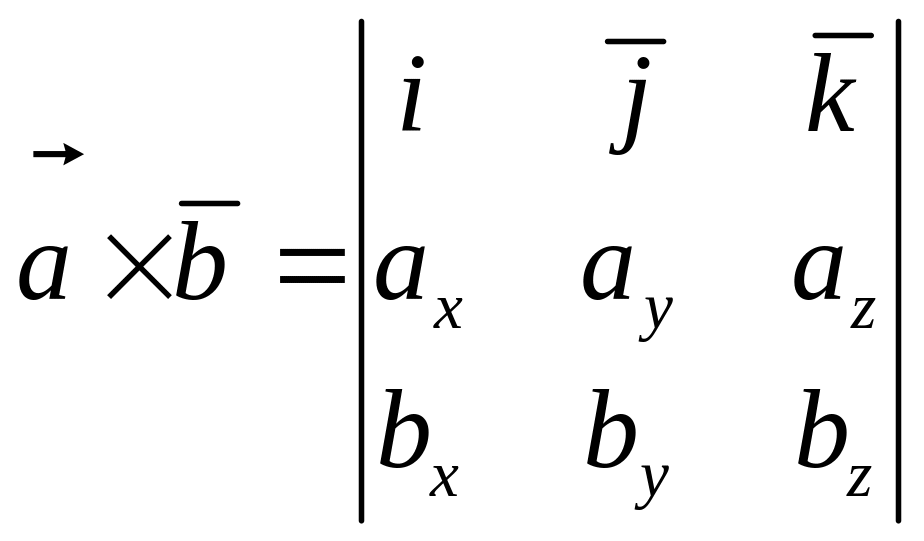
Физический смысл векторного произведения:

1. Момент.

П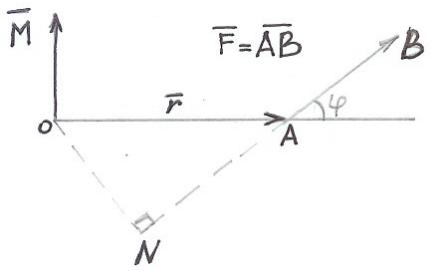 усть в точке А приложена сила = и пусть О – некоторая точка пространства.

Из физики известно, что моментом силы относительно точки О называется вектор М, который проходит через точку О и:

1) перпендикулярен плоскости, проходящей через точки О, А, В;

2)численно равен произведению силы на плечо:

3) образует правую тройку с векторами .

Стало быть, .

2. Линейная скорость вращения

С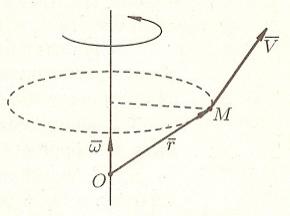 корость точки М твердого тела, вращающегося с угловой скоростью вокруг неподвижной оси , определяется формулой , где , где О – некоторая неподвижная точка оси.

7

Пусть даны три произвольных вектора a, b и с. Если вектор a векторно умножить на вектор b, а затем получившийся вектор [ab] скалярно умножается на вектор c, то в результате получается число [ab]c, называемое смешанным произведением векторов a,b и c.

 Геометрический смысл смешанного произведения:

Объем треугольной пирамиды, ребрами которой служат векторы a,b,c, равен 1/6|abc|.

Доказательство.     Построим параллелепипед, три ребра которого совпадают с тремя ребрами пирамиды, выходящими из одной точки.

Объем параллелепипеда вычисляется по формуле V_пир=S_abcdh, а объем пирамиды – V_пир=1/3S_abcdh. Так как S_abc=1/2S_abcd, то V_пир=1/6V.

Получим, что V=|abc|, а Vпир=1/6|abc|.     

Пусть в правом ортонормированном базисе i,j,k заданы векторы, a(₁,₂, ₃), b(₁, ₂, ₃) и c(₁, ₂, ₃). Тогда

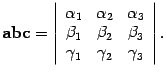
Доказательство.     Находим координаты вектора bc

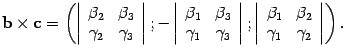
Находим скалярное произведение вектора a на вектор bc:

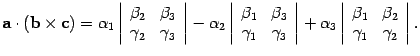
Правая часть этого равенства совпадает с определение определителя. 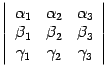По определению a(bc), формула  доказана.    

 Заметим, что если тройка векторов a,b,c является правой, то тройки c,a,b и b,c,a также будут правыми, а тройки b,a,c, c,b,a и a,c,b будут левыми тройками векторов. Так как объем параллелепипеда не зависит от того, в каком порядке перечисляются его стороны, то abc = cab = bca = -cba = -bac = -acb (*)