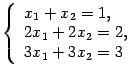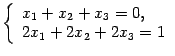1. Пусть система имеет решение. Покажем, что .

Пусть набор чисел является решением системы. Обозначим через -ый столбец матрицы , . Тогда , то есть столбец свободных членов является линейной комбинацией столбцов матрицы . Пусть . Предположим, что . Тогда по . Выберем в базисный минор . Он имеет порядок . Столбец свободных членов обязан проходить через этот минор, иначе он будет базисным минором матрицы . Столбец свободных членов в миноре является линейной комбинацией столбцов матрицы . В силу свойств определителя , где  -- определитель, который получается из минора заменой столбца свободных членов на столбец . Если столбец проходил через минор M, то в , будет два одинаковых столбца и, следовательно, . Если столбец не проходил через минор , то будет отличаться от минора порядка r+1 матрицы только порядком столбцов. Так как , то . Таким образом, , что противоречит определению базисного минора. Значит, предположение, что , неверно.

2. Пусть . Покажем, что система имеет решение. Так как , то базисный минор матрицы является базисным минором матрицы . Пусть через минор проходят столбцы . Тогда по теореме о базисном миноре в матрице столбец свободных членов является линейной комбинацией указанных столбцов:

(1)

Положим , , , , остальные неизвестные возьмем равными нулю. Тогда при этих значениях получим

В силу равенства (1) . Последнее равенство означает, что набор чисел является решением системы. Существование решения доказано.     

В рассмотренной выше системе  , и система является совместной. В системе  , , и система является несовместной.

        Замечание: Хотя теорема Кронекера-Капелли дает возможность определить, является ли система совместной, применяется она довольно редко, в основном в теоретических исследованиях. Причина заключается в том, что вычисления, выполняемые при нахождении ранга матрицы, в основном совпадают с вычислениями при нахождении решения системы. Поэтому, обычно вместо того, чтобы находить и , ищут решение системы. Если его удается найти, то узнаем, что система совместна и одновременно получаем ее решение. Если решение не удается найти, то делаем вывод, что система несовместна.         

Алгоритм нахождения решений произвольной системы линейных уравнений (метод Гаусса)

Пусть дана система линейных уравнений с неизвестными . Требуется найти ее общее решение, если она совместна, или установить ее несовместность. Метод, который будет изложен в этом разделе, близок к методу вычисления определителя и к методу нахождения ранга матрицы. Предлагаемый алгоритм называется методом Гаусса или методом последовательного исключения неизвестных.

Выпишем расширенную матрицу системы

Назовем элементарными операциями следующие действия с матрицами:

1. перестановка строк;

2. умножение строки на число, отличное от нуля;

3. сложение строки с другой строкой, умноженной на число.

Отметим, что при решении системы уравнений, в отличие от вычисления определителя и нахождения ранга, нельзя оперировать со столбцами. Если по матрице, полученной из выполнением элементарной операции, восстановить систему уравнений, то новая система будет равносильна исходной.

Цель алгоритма -- с помощью применения последовательности элементарных операций к матрице добиться, чтобы каждая строка, кроме, быть может, первой, начиналась с нулей, и число нулей до первого ненулевого элемента в каждой следующей строке было больше, чем в предыдущей.

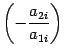Шаг алгоритма заключается в следующем. Находим первый ненулевой столбец в матрице . Пусть это будет столбец с номером . Находим в нем ненулевой элемент и строку с этим элементом меняем местами с первой строкой. Чтобы не нагромождать дополнительных обозначений, будем считать, что такая смена строк в матрице уже произведена, то есть . Тогда ко второй строке прибавим первую, умноженную на число , к третьей строке прибавим первую, умноженную на число 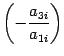, и т.д. В результате получим матрицу

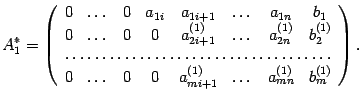
(Первые нулевые столбцы, как правило, отсутствуют.)

Если в матрице встретилась строка с номером k, в которой все элементы равны нулю, а , то выполнение алгоритма останавливаем и делаем вывод, что система несовместна. Действительно, восстанавливая систему уравнений по расширенной матрице, получим, что -ое уравнение будет иметь вид

Этому уравнению не удовлетворяет ни один набор чисел .

Матрицу можно записать в виде

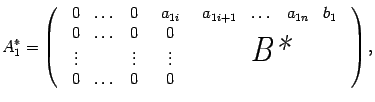
где

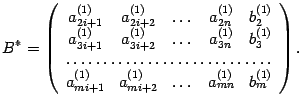
По отношению к матрице выполняем описанный шаг алгоритма. Получаем матрицу

где , . Эту матрицу снова можно записать в виде

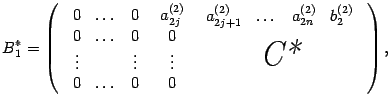
и к матрице снова применим описанный выше шаг алгоритма.

Процесс останавливается, если после выполнения очередного шага новая уменьшенная матрица состоит из одних нулей или если исчерпаны все строки. Заметим, что заключение о несовместности системы могло остановить процесс и ранее.

Если бы мы не уменьшали матрицу, то в итоге пришли бы к матрице вида

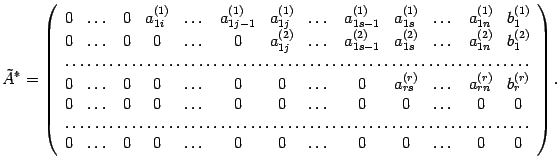
Далее выполняется так называемый обратный ход метода Гаусса. По матрице составляем систему уравнений. В левой части оставляем неизвестные с номерами, соответствующими первым ненулевым элементам в каждой строке, то есть . Заметим, что . Остальные неизвестные переносим в правую часть. Считая неизвестные в правой части некоторыми фиксированными величинами, несложно выразить через них неизвестные левой части.

Теперь, придавая неизвестным в правой части произвольные значения и вычисляя значения переменных левой части, мы будем находить различные решения исходной системы Ax=b. Чтобы записать общее решение, нужно неизвестные в правой части обозначить в каком-либо порядке буквами , включая и те неизвестные, которые явно не выписаны в правой части из-за нулевых коэффициентов, и тогда столбец неизвестных можно записать в виде столбца, где каждый элемент будет линейной комбинацией произвольных величин (в частности, просто произвольной величиной ). Эта запись и будет общим решением системы.

Если система была однородной, то получим общее решение однородной системы. Коэффициенты при , взятые в каждом элементе столбца общего решения, составят первое решение из фундаментальной системы решений, коэффициенты при  -- второе решение и т.д.

Способ 2: Фундаментальную систему решений однородной системы можно получить и другим способом. Для этого одной переменной, перенесенной в правую часть, нужно присвоить значение 1, а остальным - нули. Вычислив значения переменных в левой части, получим одно решение из фундаментальной системы. Присвоив другой переменной в правой части значение 1, а остальным - нули, получим второе решение из фундаментальной системы и т.д.

23

Определение: система называется совместной, если она имеет хотя бы одно решение, и несовместной -- в противном случае, то есть в случае, когда решений у системы нет.         Вопрос о том, имеет ли система решение или нет, связан не только с соотношением числа уравнений и числа неизвестных. Например, система из трех уравнений с двумя неизвестными

имеет решение , и даже имеет бесконечно много решений, а система из двух уравнений с тремя неизвестными

решений не имеет, то есть является несовместной.

        Определение:  Расширенной матрицей системы линейных уравнений  называется матрица , отличающаяся от матрицы системы наличием дополнительного столбца из свободных членов:

        

Следствие: Ранг расширенной матрицы либо равен рангу матрицы системы A, либо больше его на единицу.

Доказательство:  Так как любая линейно независимая система столбцов матрицы A является линейно независимой системой столбцов матрицы , то в силу предложения 14.26 (Ранг матрицы равен максимальному числу ее столбцов, образующих линейно независимую систему) .

Пусть . Предположим, что , . Тогда в матрице есть линейно независимая система из r+k столбцов. Среди этих столбцов может быть только один, не принадлежащий матрице A. Тогда подсистема остальных r+k-1 столбцов, принадлежащих матрице A , должна быть линейно независимой. Следовательно, . Получили противоречие. Предположение, что k>1, неверно.   

Квадратные системы с невырожденной матрицей.

Система называется квадратной, если число m ее уравнений равно числу n неизвестных, то есть когда ее матрица A -- квадратная матрица.

24

Решение СЛАУ: Пусть дана СЛАУ

A₁₁x₁ + … + a_1nx_n = 0

……. … ……

A_m1x₁ + … + a_mnx_n = 0

Данная система всегда совместна так как имеет тривиальное решение х₁=…=х_n=0

Для существования нетривиальных решений необходимо и достаточно выполнение

словия r = r(A) < n , что равносильно условию det(A)=0, когда матрица А – квадратная.

Th Совокупность решений СЛАУ образует линейное пространство размерности (n-r). Это означает, что произведение ее решения на число, а также сумма и линейная комбинация конечного числа ее решений является решениями этой системы. Линейное пространство решений любой СЛАУ является подпространством пространства Rⁿ.

Любая совокупность (n-r) линейно независимых решений СЛАУ (являющаяся базисом в пространстве решений) называется фундаментальной совокупностью решений(ФСР).

Пусть х₁,…,х_r - базисные неизвестные, х_r+1,…,х_n – свободные неизвестные. Свободным переменным дадим поочередно следующие значения:

х_r+1=1 х_r+1=0 х_r+1=0

х_r+2=0 х_r+2=1 х_r+2=0

…… …… ……

х_n=0 х_n=0 х_n=1

Определив значения базисных переменных, соответствующие каждому набору значений свободных переменных, получим решения:

Х₁ ⁽¹⁾ Х₁ ⁽²⁾ Х₁ ^(n-r)

…… …… …….

Х⁽¹⁾ = Х_r ⁽¹⁾ , Х⁽²⁾ = Х_r ⁽²⁾ ,…, Х^(n-r) = Х_r ^(n-r)

1 0 0

0 1 0

0 0 1

Построенная таким образом система решений системы уравнений называется нормальной фундаментальной совокупностью решений.

Теорема. Множество всех решений однородной системы уравнений

A₁₁x₁ + … + a_1nx_n = 0

……. … ……

A_m1x₁ + … + a_mnx_n = 0

Образует линейное пространство S (пространство решений), которое является подпространством в Rⁿ (n – число неизвестных), причем dims=k=n-r, где r- ранг системы. Базис в пространстве решений{x ⁽¹⁾,…, x ^(k)} называется фундаментальной системой решений, и общее решение имеет вид:

X=c₁x ⁽¹⁾ + … + c_kx ^(k), c ⁽¹⁾,…, c ^(k) € R

25