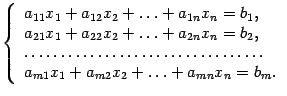Системы линейных уравнений

Определение: Системой линейных уравнений с неизвестными называется система уравнений вида

(1)

Систему (1) можно записать также в виде

или в виде

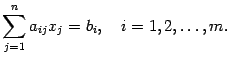
Но наиболее удобной формой записи системы (15.1) является матричная запись. Введем следующие матрицы: матрица системы , столбец неизвестных и столбец свободных членов ,

с помощью введенных обозначений систему (1) можно записать в виде

Ax=b

Однородная, неоднородная СЛАУ. Система уравнений называется однородной, если и неоднородной в противном случае.     

Совместная, несовместная СЛАУ.

Система называется совместной, или разрешимой, если она имеет по крайней мере одно решение. Система называется несовместной, или неразрешимой, если она не имеет решений.

Определённая, неопределённая СЛАУ.

Если СЛАУ имеет решение и при том единственное, то её называют определённой а если решение неединственное – то неопределённой.

МАТРИЧНЫЕ УРАВНЕНИЯ

Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:

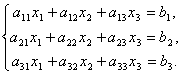Рассмотрим матрицу системы 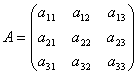и матрицы столбцы неизвестных и свободных членов

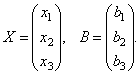
Найдем произведение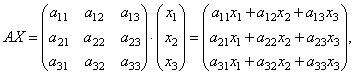

т.е. в результате произведения мы получаем левые части уравнений данной системы. Тогда пользуясь определением равенства матриц данную систему можно записать в виде

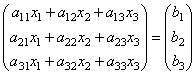или короче A∙X=B.

Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением.

Пусть определитель матрицы отличен от нуля |A| ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A^-1, обратную матрице A: . Поскольку A^-1A = E и E∙X = X, то получаем решение матричного уравнения в виде X = A^-1B.

Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных.

Формулы Крамера

Метод Крамера состоит в том, что мы последовательно находим главный определитель системы, т.е. определитель матрицы А :  = det (a_{i j}) и n вспомогательных определителей  _i (i= ), которые получаются из определителя  заменой i-го столбца столбцом свободных членов.

Формулы Крамера имеют вид:   x _i =  _i (i = ).

Из этого следует правило Крамера, которое дает исчерпывающий ответ на вопрос о совместности системы: если главный определитель системы отличен от нуля, то система имеет единственное решение, определяемое по формулам: x _i =  _i / .

Если главный определитель системы  и все вспомогательные определители  _i = 0 (i= ), то система имеет бесчисленное множество решений. Если главный определитель системы  = 0, а хотя бы один вспомогательный определитель отличен от нуля, то система несовместна.

Теорема (правило Крамера): Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём

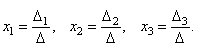
Доказательство: Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A₁₁ элемента a₁₁, 2-ое уравнение – на A₂₁ и 3-е – на A₃₁:

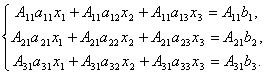
Сложим эти уравнения:

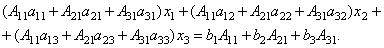
Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца .

Далее рассмотрим коэффициенты при x₂:

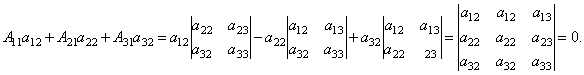
Аналогично можно показать, что и .

Наконец несложно заметить, что

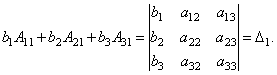
Таким образом, получаем равенство: . Следовательно, .

Аналогично выводятся равенства и , откуда и следует утверждение теоремы.

22

Теорема Кронекера - Капелли.

Система линейных уравнений  является совместной тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы .

Доказательство: Оно распадается на два этапа.