
- •Неравенство треугольника:
- •Линейная комбинация векторов:
- •Критерий линейной зависимости 2ух векторов:
- •Следствия:
- •Свойства линейно зависимых и линейно независимых векторов:
- •Критерий зависимости 2ух векторов:
- •Критерий зависимости 3ех векторов:
- •Линейная зависимость 4ех векторов:
- •Cвойства смешанного произведения:
- •Смешанное произведение векторов равно нулю тогда и только тогда, когда сомножители a,b,c компланарны.
- •Смешанное произведение в ортонормированном базисе:
- •Уравнение прямой с угловым коэффициентом.
- •Общее уравнение прямой.
- •Уравнение прямой, проходящей через две заданные точки
- •Условие параллельности двух прямых.
- •Уравнение плоскости, проходящей через три различные точки, не лежащие на одной прямой:
- •Расстояние от точки до плоскости
- •Уравнение прямой, проходящей через две заданные точки
- •Взаимное расположение прямых и плоскостей в пространстве.
- •Нахождение угла между плоскостями. Косинус угла между двумя плоскостями
- •Эллипс: эллипсом называется множество точек плоскости, сумма расстояний от которых до двух данных точек, называемых фокусами эллипса, есть величина постоянная.
- •Выведение канонического уравнения эллипса:
- •Свойства определителей:
- •Умножение матриц обладает следующими свойствами:
- •Теорема о базисном миноре.
- •Ранг ступенчатой матрицы.
- •Системы линейных уравнений
- •Формулы Крамера
- •1. Пусть система имеет решение. Покажем, что .
- •Алгоритм нахождения решений произвольной системы линейных уравнений (метод Гаусса)
- •Теорема о связи решений неоднородной и соответствующей однородной слау
- •Вид общего решения неоднородной слау
Теорема о базисном миноре.
Любой столбец матрицы является линейной комбинацией столбцов, проходящих через базисный минор.
Следствие1: Ранг матрицы равен максимальному числу ее столбцов, образующих линейно независимую систему.
Доказательство: Пусть ранг матрицы равен . Возьмем столбцы, проходящие через базисный минор. Предположим, что эти столбцы образуют линейно зависимую систему. Тогда один из столбцов является линейной комбинацией других. Поэтому в базисном миноре один столбец будет линейной комбинацией других столбцов. Этот базисный минор должен быть равен нулю, что противоречит определению базисного минора. Следовательно, предположение о том, что столбцы, проходящие через базисный минор, линейно зависимы, не верно. Итак, максимальное число столбцов, образующих линейно независимую систему, больше либо равно . Предположим, что столбцов образуют линейно независимую систему. Составим из них матрицу . Все миноры матрицы являются минорами матрицы . Поэтому базисный минор матрицы имеет порядок не больше . По теореме о базисном миноре, столбец, не проходящий через базисный минор матрицы , является линейной комбинацией столбцов, проходящих через базисный минор, то есть столбцы матрицы образуют линейно зависимую систему. Это противоречит выбору столбцов, образующих матрицу . Следовательно, максимальное число столбцов, образующих линейно независимую систему, не может быть больше . Значит, оно равно , что и утверждалось.
Следствие2: Ранг матрицы равен максимальному числу ее строк, образующих линейно независимую систему.
Доказательство: Ранг матрицы при транспонировании не меняется. Строки матрицы становятся ее столбцами. Максимальное число новых столбцов транспонированной матрицы, (бывших строк исходной) образующих линейно независимую систему, равно рангу матрицы.
Следствие3: Если определитель матрицы равен нулю, то один из его столбцов (одна из строк) является линейной комбинацией остальных столбцов (строк).
Доказательство: Пусть порядок
матрицы
равен
.
Определитель является единственным
минором квадратной матрицы, имеющим
порядок
.
Так как он равен нулю, то
![]() .
Следовательно, система из
столбцов
(строк) является линейно зависимой, то
есть один из столбцов (одна из строк)
является линейной комбинацией остальных.
.
Следовательно, система из
столбцов
(строк) является линейно зависимой, то
есть один из столбцов (одна из строк)
является линейной комбинацией остальных.
Теорема: Определитель матрицы равен нулю тогда и только тогда, когда один из ее столбцов (одна из строк) является линейной комбинацией остальных столбцов (строк).
Ранг ступенчатой матрицы.
Вспомним, что матрица вида
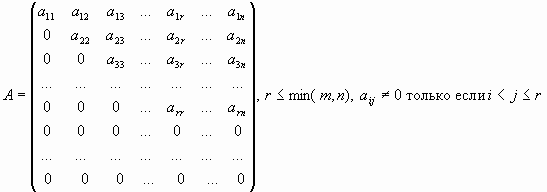
называется ступенчатой матрицей.
Очевидно, что ранг ступенчатой матрицы равен числу ненулевых строк.
Поскольку доказано, что любую матрицу с помощью элементарных преобразований можно привести к ступенчатому виду, а элементарные преобразования не меняют ранга матрицы, то можно дать еще одно эквивалентное определение ранга матицы: ранг матрицы равен числу ненулевых строк в ступенчатой форме матрицы.
Это последнее определение позволяет вычислять ранг матрицы с помощью Гауссова исключения: для того, чтобы вычислить ранг матрицы, приводим ее Гауссовым исключением к ступенчатому виду и подсчитываем количество ненулевых строк.
Ранг матрицы находится:
либо методом окаймления миноров,
либо методом элементарных преобразований.
1) При вычислении ранга матрицы первым способом следует переходить от миноров низших порядков к минорам более высокого порядка. Если уже найден минор D k-го порядка матрицы А, отличный от нуля, то требуют вычисления лишь миноры (k+1)-го порядка, окаймляющие минор D, т.е. содержащие его в качестве минора. Если все они равны нулю, то ранг матрицы равен k.
Пример:
Найти методом
окаймления миноров
ранг матрицы
![]() .
.
Решение.
Начинаем с
миноров 1-го порядка, т.е. с элементов
матрицы А. Выберем, например, минор
(элемент) М1
= 1, расположенный в первой строке и
первом столбце. Окаймляя при помощи
второй строки и третьего столбца,
получаем минор M2
=
![]() ,
отличный от нуля. Переходим теперь к
минорам 3-го порядка, окаймляющим М2.
Их всего два (можно
добавить второй
столбец или четвертый). Вычисляем их:
0. Таким образом, все окаймляющие миноры
третьего порядка оказались равными
нулю. Ранг матрицы А равен двум.
,
отличный от нуля. Переходим теперь к
минорам 3-го порядка, окаймляющим М2.
Их всего два (можно
добавить второй
столбец или четвертый). Вычисляем их:
0. Таким образом, все окаймляющие миноры
третьего порядка оказались равными
нулю. Ранг матрицы А равен двум.
2) Элементарными называются следующие преобразования матрицы:
1) перестановка двух любых строк (или столбцов),
2) умножение строки (или столбца) на отличное от нуля число,
3) прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число.
Две матрицы называются эквивалентными, если одна из них получается из другой с помощью конечного множества элементарных преобразований. Эквивалентные матрицы не являются, вообще говоря, равными, но их ранги равны. Если матрицы А и В эквивалентны, то это записывается так: A B.
Алгоритм нахождения ранга матрицы.
Пусть требуется вычислить ранг матрицы
размеров
.
Если матрица
- нулевая, то по определению
![]() .
В противном случае с помощью перестановки
строк и столбцов матрицы добиваемся
того, чтобы в левом верхнем углу матрицы
стоял ненулевой элемент. Итак, считаем,
что
.
В противном случае с помощью перестановки
строк и столбцов матрицы добиваемся
того, чтобы в левом верхнем углу матрицы
стоял ненулевой элемент. Итак, считаем,
что
![]() .
.
Первую строку оставляем без изменений.
Ко второй строке прибавляем первую,
умноженную на число
 .
В результате вторая строка принимает
вид
.
В результате вторая строка принимает
вид
 Затем
к третьей строке прибавляем первую
строку, умноженную на число
Затем
к третьей строке прибавляем первую
строку, умноженную на число
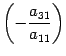 .
В результате третья строка принимает
вид
.
В результате третья строка принимает
вид

Процесс продолжаем до тех пор, пока не получим нуль на первом месте в последней строке.
Преобразованная матрица имеет вид
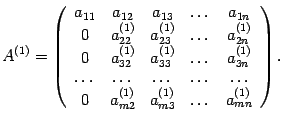
Если все строки, начиная со второй, в
полученной матрице нулевые, то ее ранг
равен 1, так как есть минор первого
порядка, отличный от нуля
![]() .
В противном случае перестановкой строк
и столбцов матрицы с номерами, большими
единицы, добиваемся, чтобы второй элемент
второй строки был отличен от нуля. Итак,
считаем, что
.
В противном случае перестановкой строк
и столбцов матрицы с номерами, большими
единицы, добиваемся, чтобы второй элемент
второй строки был отличен от нуля. Итак,
считаем, что
![]() .
Первую и вторую строки оставляем без
изменений. К третьей строке прибавляем
вторую, умноженную на число
.
Первую и вторую строки оставляем без
изменений. К третьей строке прибавляем
вторую, умноженную на число
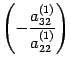 .
В результате получим, что второй элемент
третьей строки равен нулю. Затем к
четвертой строке прибавляем вторую,
умноженную на число
.
В результате получим, что второй элемент
третьей строки равен нулю. Затем к
четвертой строке прибавляем вторую,
умноженную на число
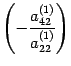 ,
и т.д. В результате получаем матрицу
,
и т.д. В результате получаем матрицу
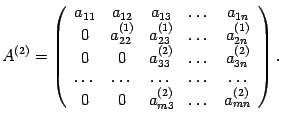
Если все строки, начиная с третьей,
нулевые, то
![]() ,
так как минор
,
так как минор
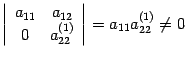 .
В противном случае перестановкой строк
и столбцов с номерами, большими двух,
добиваемся, чтобы третий элемент третьей
строки был отличен от нуля. Далее,
добавлением третьей строки, умноженной
на соответствующие числа, к строкам с
большими номерами получаем нули в
третьем столбце, начиная с четвертого
элемента, и т.д.
.
В противном случае перестановкой строк
и столбцов с номерами, большими двух,
добиваемся, чтобы третий элемент третьей
строки был отличен от нуля. Далее,
добавлением третьей строки, умноженной
на соответствующие числа, к строкам с
большими номерами получаем нули в
третьем столбце, начиная с четвертого
элемента, и т.д.
На каком-то этапе мы придем к матрице,
у которой все строки, начиная с
![]() -ой
, равны нулю (или отсутствуют при
-ой
, равны нулю (или отсутствуют при
![]() ),
а минор в первых
строках
и первых
столбцах
является определителем треугольной
матрицы с ненулевыми элементами на
диагонали. Ранг такой матрицы равен
.
Следовательно,
),
а минор в первых
строках
и первых
столбцах
является определителем треугольной
матрицы с ненулевыми элементами на
диагонали. Ранг такой матрицы равен
.
Следовательно,
![]() .
.
20
Ранг и базис системы векторов
Определение 1.
Рангом
системы векторов называется максимальное
число линейно
независимых векторов (Система векторов
![]() называется линейно зависимой, если один
из векторов системы можно представить
в виде линейной комбинации остальных
векторов системы, и линейно независимой
- в противном случае) системы.
называется линейно зависимой, если один
из векторов системы можно представить
в виде линейной комбинации остальных
векторов системы, и линейно независимой
- в противном случае) системы.
![]() .
.
Определение 2. Базисом системы векторов называется максимальная линейно независимая подсистема данной системы векторов.
Теорема. Любой вектор системы можно представить в виде линейной комбинации (Линейной комбинацией системы векторов называется выражение вида
![]() ,
где с1, с2, …, сk
- некоторые числа) векторов базиса
системы. (Всякий вектор системы можно
разложить по векторам базиса.) Коэффициенты
разложения определяются для данного
вектора и данного базиса однозначно.
,
где с1, с2, …, сk
- некоторые числа) векторов базиса
системы. (Всякий вектор системы можно
разложить по векторам базиса.) Коэффициенты
разложения определяются для данного
вектора и данного базиса однозначно.
Доказательство.
Пусть система
![]() имеет базис
.
имеет базис
.
1 случай. Вектор
![]() - из базиса. Следовательно, он равен
одному из векторов базиса, допустим
- из базиса. Следовательно, он равен
одному из векторов базиса, допустим
![]() .
Тогда
=
.
Тогда
=![]() .
.
2 случай. Вектор
![]() - не из базиса. Тогда r>k.
- не из базиса. Тогда r>k.
Рассмотрим систему векторов
![]() .
Данная система является
линейно зависимой, так как
.
Данная система является
линейно зависимой, так как
![]() - базис, т.е. максимальная линейно
независимая подсистема. Следовательно,
найдутся числа
с1, с2, …, сk,
с, не все равные нулю, такие, что
- базис, т.е. максимальная линейно
независимая подсистема. Следовательно,
найдутся числа
с1, с2, …, сk,
с, не все равные нулю, такие, что
![]() =
=
![]() .
Очевидно, что
.
Очевидно, что
![]() (если с=0, то базис системы является
линейно зависимым).
(если с=0, то базис системы является
линейно зависимым).
![]() .
.
Докажем, что разложение вектора по базису единственно. Предположим противное: имеется два разложения вектора по базису.
=![]() ,
=
,
=![]() .
.
Вычитая эти равенства, получим
![]() .
.
Учитывая линейную независимость векторов
базиса, получим
![]() .
.
Следовательно, разложение вектора по базису единственно.
Количество векторов в любом базисе системы одинаково и равно рангу системы векторов.
Вычисление ранга системы векторов можно свести к вычислению ранга матрицы. Т.к. ранг системы векторов равен рангу матрицы, столбцами (строками) которой являются векторы этой системы.
Пример. Найти ранг системы векторов

Составим матрицу из координат векторов и найдем ее ранг.
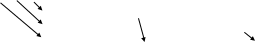
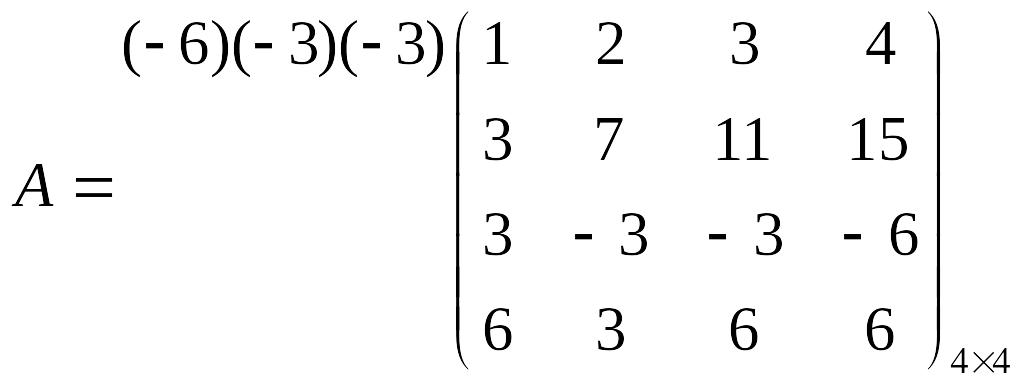 ~
~ ~
~ ~
~
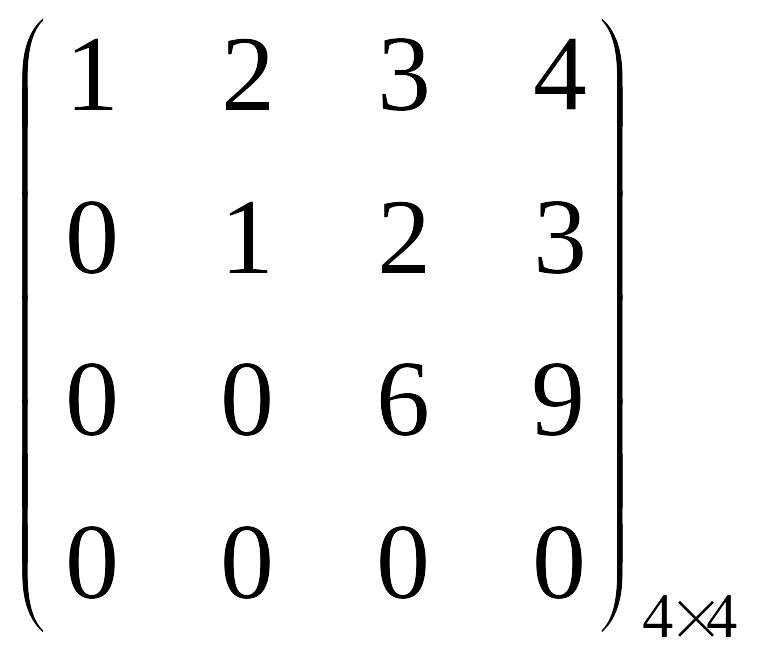 ~
~ ,
r(А)=3,
,
r(А)=3,
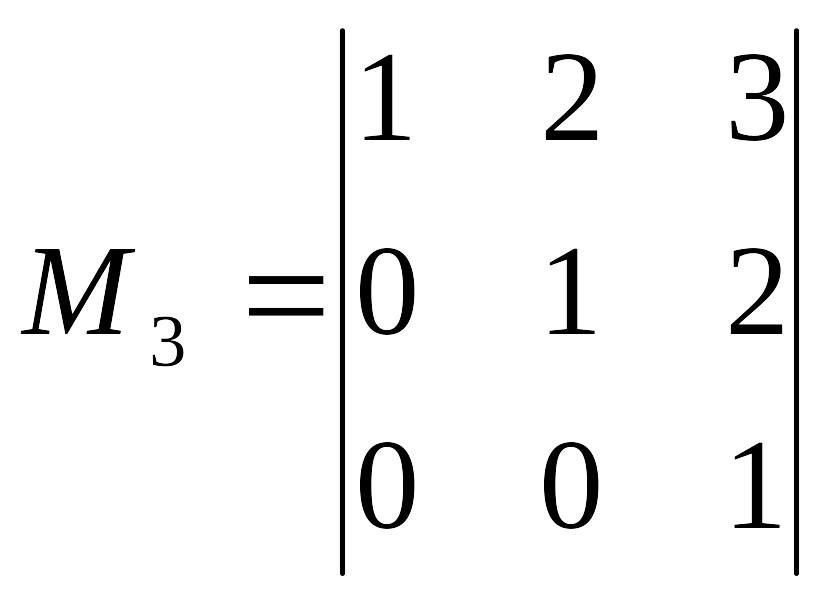 =1¹0.
=1¹0.
Ранг данной системы векторов равен трем, т.е. она имеет три линейно независимых вектора.
21
