
- •Неравенство треугольника:
- •Линейная комбинация векторов:
- •Критерий линейной зависимости 2ух векторов:
- •Следствия:
- •Свойства линейно зависимых и линейно независимых векторов:
- •Критерий зависимости 2ух векторов:
- •Критерий зависимости 3ех векторов:
- •Линейная зависимость 4ех векторов:
- •Cвойства смешанного произведения:
- •Смешанное произведение векторов равно нулю тогда и только тогда, когда сомножители a,b,c компланарны.
- •Смешанное произведение в ортонормированном базисе:
- •Уравнение прямой с угловым коэффициентом.
- •Общее уравнение прямой.
- •Уравнение прямой, проходящей через две заданные точки
- •Условие параллельности двух прямых.
- •Уравнение плоскости, проходящей через три различные точки, не лежащие на одной прямой:
- •Расстояние от точки до плоскости
- •Уравнение прямой, проходящей через две заданные точки
- •Взаимное расположение прямых и плоскостей в пространстве.
- •Нахождение угла между плоскостями. Косинус угла между двумя плоскостями
- •Эллипс: эллипсом называется множество точек плоскости, сумма расстояний от которых до двух данных точек, называемых фокусами эллипса, есть величина постоянная.
- •Выведение канонического уравнения эллипса:
- •Свойства определителей:
- •Умножение матриц обладает следующими свойствами:
- •Теорема о базисном миноре.
- •Ранг ступенчатой матрицы.
- •Системы линейных уравнений
- •Формулы Крамера
- •1. Пусть система имеет решение. Покажем, что .
- •Алгоритм нахождения решений произвольной системы линейных уравнений (метод Гаусса)
- •Теорема о связи решений неоднородной и соответствующей однородной слау
- •Вид общего решения неоднородной слау
Умножение матриц обладает следующими свойствами:
![]() --
ассоциативность умножения;
--
ассоциативность умножения;
![]() ,
где
,
где
![]() --
число;
--
число;
![]() ,
,
![]() --
дистрибутивность умножения;
--
дистрибутивность умножения;
![]() ,
,
![]() ,
где
--
единичная матрица соответствующего
порядка. Предполагается, что все указанные
произведения имеют смысл.
,
где
--
единичная матрица соответствующего
порядка. Предполагается, что все указанные
произведения имеют смысл.
Матрица
называется
обратной
матрицей для квадратной
матрицы
,
если
![]() .
.
Если матрица
имеет
обратную, то
и
![]() .
.
Если определитель матрицы равен нулю, то обратная к ней не существует.
Если обратная матрица существует, то она единственна.
Доказательство. Пусть две матрицы и являются обратными для матрицы . Тогда
![]() и
и![]()
Следовательно,
![]() .
.
Обратная матрица для квадратной матрицы существует тогда и только тогда, когда матрица -- невырожденная, обратная матрица единственна, и справедлива формула.
Присоединенной матрицей называют матрицу A* , транспонированную к матрице (Aij) алгебраических дополнений.
Метод нахождения обратной матрицы с помощью элементарных преобразований. Чтобы найти матрицу A-1 обратную к А, фактически надо решить матричное уравнение AX = E. Отметим, что если над матрицей А выполняется какое-либо элементарное преобразование строк, то это же преобразование осуществляется и над матрицей AX, поскольку любое элементарное преобразование строк матрицы эквивалентно умножению её слева на соответствующую матрицу специального вида. Таким образом, уравнение AX = E над матрицами A и E одновременно выполнить какое-либо элементарное преобразование строк, т.е. домножить это равенство слева на некоторую матрицу специального вида, то в результате получится новое матричное уравнение A1X = B1. Оба эти матричные уравнения имеют одно и то же решение, так как любое элементарное преобразование строк. Последовательность элементарных преобразований строк надо подобрать так, чтобы на s – м шаге матрицы A превратилась единичную матрицу. В результате этих s шагов получается уравнение AsX = Bs, где As = E, т.е X = Bs . Итак, поскольку А-1 является решением уравнения AX = E, которое эквивалентно X = Bs, то A-1 = Bs.
Теорема о матрице, обратной произведению двух обратимых матриц. Если квадратные матрицы A и В порядка n имеют обратные матрицы, то и их произведение имеет обратную матрицу, причём (АВ)-1 = В-1*А-1. Док-во. В соответствии с определением единственности обратной матрицы достаточно доказать два равенства:
(АВ) В-1*А-1 = Е, (В-1*А-1)(АВ) = Е. Использую ассоциативность умножения матриц получаем: (АВ) В-1*А-1 = А(ВВ-1)А-1 = АЕА-1 = АА-1 = Е ,
(В-1*А-1)(АВ) = В-1(А-1А)В = В-1ЕВ = В-1В = Е . Что и требовалось доказать.
Теорема о транспонировании обратной матрицы. Если матрица А порядка n имеет обратную, то и транспонированная матрица AT имеет обратную , причём
(AT) -1 = (А-1) T. Док-во. Нужно убедиться, что АT (А-1) T = Е и (А-1) TА T = Е. Используя свойство произведения матриц относительно операции транспонирования имеем: АT (А-1) T = (А-1А)Т = ЕТ = Е , (А-1)ТАТ= (АА-1)Т = ЕТ = Е
19
МИНОР:
Пусть дана матрица
размеров
и
число k, не превосходящее
наименьшего из чисел
![]() и
:
и
:
![]() .
Выберем произвольно
строк
матрицы
и
столбцов
(номера строк могут отличаться от номеров
столбцов). Определитель матрицы,
составленной из элементов, стоящих на
пересечении выбранных
строк
и
столбцов,
называется минором порядка
матрицы
.
.
Выберем произвольно
строк
матрицы
и
столбцов
(номера строк могут отличаться от номеров
столбцов). Определитель матрицы,
составленной из элементов, стоящих на
пересечении выбранных
строк
и
столбцов,
называется минором порядка
матрицы
.
Пример:
Пусть
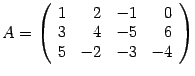 .
.
Минором первого порядка является любой элемент матрицы. Так 2, -5, -4 - миноры первого порядка.
Миноры второго порядка:
возьмем строки 1, 2, столбцы 1, 2, получим минор
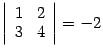 ;
;
возьмем строки 1, 3, столбцы 2, 4, получим минор
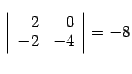 ;
;
возьмем строки 2, 3, столбцы 1, 4, получим минор
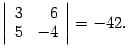
Миноры третьего порядка:
строки здесь можно выбрать только одним способом,
возьмем столбцы 1, 3, 4, получим минор
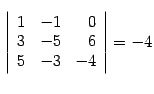 ;
;
возьмем столбцы 1, 2, 3, получим минор
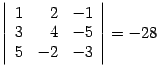 .
.
РАНГ МАТРИЦЫ: Рангом матрицы называется наибольший из порядков миноров матрицы , отличных от нуля. Ранг нулевой матрицы считается равным нулю. Ранг матрицы обозначается так: R(A).
Пример: Матрица имеет ранг 3, так как есть минор третьего порядка, отличный от нуля, а миноров четвертого порядка нет.
Ранг матрицы
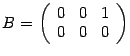 равен
1, так как есть ненулевой минор первого
порядка (элемент матрицы
равен
1, так как есть ненулевой минор первого
порядка (элемент матрицы
![]() ),
а все миноры второго порядка равны нулю.
),
а все миноры второго порядка равны нулю.
Ранг невырожденной квадратной матрицы порядка равен , так как ее определитель является минором порядка и у невырожденной матрицы отличен от нуля.
Следствие:
При транспонировании матрицы ее ранг
не меняется, то есть
![]() .
.
Доказательство.
Транспонированный минор исходной
матрицы
будет являться минором транспонированной
матрицы
,
и наоборот, любой минор
является
транспонированным минором исходной
матрицы
.
При транспонировании определитель
(минор) не меняется. Поэтому если все
миноры порядка
![]() в
исходной матрице равны нулю, то все
миноры того же порядка в
тоже
равны нулю. Если же минор порядка
в
исходной матрице равны нулю, то все
миноры того же порядка в
тоже
равны нулю. Если же минор порядка
![]() в
исходной матрице отличен от нуля, то в
есть минор того же порядка, отличный от
нуля. Следовательно,
.
в
исходной матрице отличен от нуля, то в
есть минор того же порядка, отличный от
нуля. Следовательно,
.
Базисный минор: Пусть ранг матрицы равен . Тогда любой минор порядка , отличный от нуля, называется базисным минором.
Пример:
Пусть
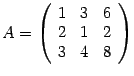 .
Определитель матрицы
равен нулю, так как третья строка равна
сумме первых двух. Минор второго порядка,
расположенный в первых двух строках и
первых двух столбцах, равен
.
Определитель матрицы
равен нулю, так как третья строка равна
сумме первых двух. Минор второго порядка,
расположенный в первых двух строках и
первых двух столбцах, равен
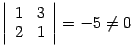 .
Следовательно, ранг матрицы равен двум,
и рассмотренный минор является базисным.
.
Следовательно, ранг матрицы равен двум,
и рассмотренный минор является базисным.
Базисным минором является также минор,
расположенный, скажем, в первой и третьей
строках, первом и третьем столбцах:
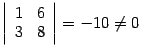 .
Базисным будет минор во второй и третьей
строках, первом и третьем столбцах:
.
Базисным будет минор во второй и третьей
строках, первом и третьем столбцах:
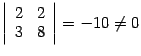 .
.
Минор в первой и второй строках, втором
и третьем столбцах
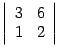 равен
нулю и поэтому не будет базисным.
равен
нулю и поэтому не будет базисным.
Линейная зависимость строк и столбцов. Строки и столбцы матрицы можно рассматривать как матрицы – строки и матрицы – столбцы, соответственно над ними тоже можно выполнять линейные операции. Ограничение на операцию сложения состоит лишь в том, что строки (столбцы) должны быть одинаковой длины (высоты), но это условие всегда выполняется для строк (столбцов) одной матрицы.
Система столбцов (строк) является линейно зависимой тогда и только тогда, когда один из столбцов (одна из строк) является линейной комбинацией других столбцов (строк) этой системы.
Строки (столбцы) a1 … as называют линейно зависимыми, если равенство λ1a1 + … + λ2as =0
Где 0 в правой части – нулевая строка (столбец), возможно лишь при λ1 = … = λs = 0. В противном случае, когда существуют такие действительные числа λ1 … λs, не равные нулю одновременно, что выполняется равенство (λ1a1 + … + λ2as =0), эти строки (столбцы) называют линейно зависимыми.
Теорема1: Строки (столбцы) линейно зависимы тогда и только тогда, когда хотя бы одна (один) из них является линейной комбинацией остальных.
Доказательство: Если строки a1, … as линейно зависимы, то согласно определению линейно независимых строк, существуют такие действительные числа λ1, … λs, не равные нулю одновременно, что λ1a1 + … + λsas = 0. Выберем ненулевой коэффициент λi. Для простоты пусть это будет λ1. Тогда: λ1a1 = (-λ2)a2 + … + (-λs)as, и следовательно a1 = (-λ2/λ1)a2 + … + (-λs/λ1)as, т.е строка a1 представляется в виде линейной комбинации остальных строк.
Теорема2: Пусть строки (столбцы) a1, … as а каждая из строк (столбцов) b1, … bl являются их линейной комбинацией. Тогда все строки (столбцы) a1, … as , b1, … bl линейно зависимы.
Доказательство: По условию b1 есть линейная комбинация a1, … as т.е b1 = λ1a1 + … + λ2as . В эту линейную комбинацию добавим строки (столбцы) b2 … bl (при l>1) с нулевыми коэффициентами. b1 = λ1a1 + … + λ2as + 0 b2 + … + 0 bl. Согласно Теореме1 строки (столбцы)
a1, … as , b1, … bl линейно зависимы.
