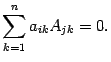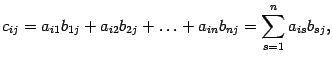Свойства определителей:

1. Определитель не меняется при транспонировании.

2. Если одна из строк определителя состоит из нулей, то определитель равен нулю.

3. Если в определителе переставить две строки, определитель поменяет знак.

4. Определитель, содержащий две одинаковые строки, равен нулю.

5. Если все элементы некоторой строки определителя умножить на некоторое число k, то сам определитель умножится на k.

6. Определитель, содержащий две пропорциональные строки, равен нулю.

7. Если все элементы i-й строки определителя представлены в виде суммы двух слагаемых a_{i j} = b_j + c_j (j= ), то определитель равен сумме определителей, у которых все строки, кроме i-ой, - такие же, как в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов b_j, в другом - из элементов c_j.

8. Определитель не меняется, если к элементам одной из его строк прибавляются соответствующие элементы другой строки, умноженные на одно и то же число. Разложение определителя по произвольной строке: Для определителя матрицы справедлива формула

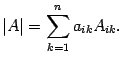  Доказательство.     Если , положим . Пусть . Тогда -ую строку поменяем местами со строкой с номером . Определитель сменит знак. Затем строку с номером поменяем местами со строкой с номером . Определитель снова сменит знак. Процесс перестановки строк будем продолжать до тех пор, пока -ая строка матрицы не станет первой строкой новой матрицы, которую мы обозначим . Отметим, что в матрице , начиная со второй строки, стоят строки матрицы , причем порядок их следования не изменился.

При переходе от матрицы к матрице определитель сменит знак раз (проверьте для случая ). Таким образом

(14.11)

Это соотношение верно и при . По определению определителя,

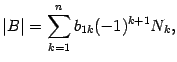где  -- определитель матрицы, полученной из матрицы вычеркиванием первой строки и k-ого столбца. Первая строка матрицы совпадает с -ой строкой матрицы , поэтому . Результат вычеркивания в матрице первой строки и k-ого столбца будет таким же, как при вычеркивании в матрице -ой строки и -ого столбца. Поэтому , где  -- определитель матрицы, полученной при вычеркивании в матрице -ой строки и -ого столбца. Следовательно,

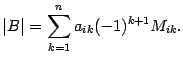
В силу равенства (14.11) получим

По определению алгебраического дополнения получим . Тогда из предыдущего равенства вытекает

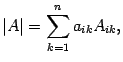что и требовалось доказать.

Определитель построенной матрицы обозначают М_ij и называют минором, соответствующим элементу a_ij . Число А_ij = (-1)^i+jМ_ij называют алгебраическим дополнением, соответствующим этому же элементу a_ij

Для квадратной матрицы порядка при выполнено соотношение

 Доказательство.     Пусть  -- матрица, полученная из матрицы , в которой -ая строка заменена -ой строкой этой же матрицы, а сама -ая строка осталась без изменения. Таким образом, в матрице есть две одинаковые строки и в силу  предложения 14.9 .

С другой стороны, используя разложение определителя по -ой строке , получим

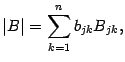
где  -- алгебраическое дополнение к элементу . Так как все строки матрицы , кроме -ой, совпадают со строками матрицы , то . Так как по построению матрицы , то

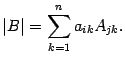
Так как , то равенство (14.12) доказано.    

Все свойства определителя, сформулированные для строк , справедливы и для столбцов, в частности, справедливо разложение определителя по -ому столбцу

Определитель треугольной матрицы равен произведению элементов ее главной диагонали.

        Доказательство.     Воспользуемся индукцией по порядку матрицы. Для :

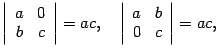
утверждение верно. Предположим, что доказываемое утверждение верно для матриц порядка . Покажем, что оно верно для матрицы порядка .

Если -- верхняя треугольная матрица, то используем разложение по первому столбцу (равенство (14.13) при ):

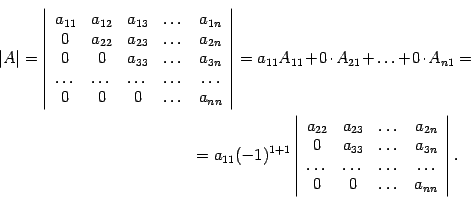
Справа стоит определитель треугольной марицы порядка . По предположению индукции этот определитель равен . Поэтому .

Если  -- нижняя треугольная матрицы, то нужно воспользоваться разложением по первой строке. В остальном рассуждения аналогичны.

Итак, утверждение верно для матрицы порядка . Предложение доказано

Определитель единичной матрицы равен единице, .     

Определитель n –ого порядка.

A = ,в котором все элементы по одну сторону от главной диагонали равны нулю.

Решение. Разложим определитель А по первой строке:

A = a₁₁ A₁₁ = .

Определитель, стоящий справа, можно снова разложить по первой строке, тогда получим:

A = .И так далее. После n шагов придем к равенству A = а₁₁ а_22... a_nn.

С помощью элементарных преобразований строк любая матрица приводится к ступенчатому виду. Квадратная матрица ступенчатого вида является частным случаем верхней треугольной матрицы, у которой диагональные элементы, начиная с некоторого, могут быть равны нулю. Определитель такой матрицы считается как определитель треугольной матрицы.

Квадратную матрицу назовем вырожденной или особенной матрицей, если , и невырожденной или неособенной матрицей, если

18

Произведением матрицы размеров на матрицу размеров называется матрица размеров , элементы которой вычисляются по формуле

где , .

Во-первых, в этом определении нужно обратить внимание на то, что важен порядок сомножителей, нужно знать, какой сомножитель первый, а какой второй.

Во-вторых, нужно отметить, что произведение определено только в том случае, если число столбцов первого сомножителя равно числу строк второго. Если это условие не выполняется, то произведение не определено.

В-третьих, размеры результата умножения определяются следующим образом: число строк результата равно числу строк первого сомножителя, а число столбцов результата равно числу столбцов второго сомножителя.

Правило вычисления элементов произведения можно сформулировать следующим образом:Для того, чтобы вычислить элемент произведения, стоящий в i-ой строке и j-ом столбце, нужно взять -ую строку первого сомножителя и j-ый столбец второго сомножителя, попарно перемножить их элементы, стоящие на одинаковых местах, и результаты сложить.

Легко проверить, что произведение квадратных матриц одного порядка всегда существует (определено).