- •Неравенство треугольника:
- •Линейная комбинация векторов:
- •Критерий линейной зависимости 2ух векторов:
- •Следствия:
- •Свойства линейно зависимых и линейно независимых векторов:
- •Критерий зависимости 2ух векторов:
- •Критерий зависимости 3ех векторов:
- •Линейная зависимость 4ех векторов:
- •Cвойства смешанного произведения:
- •Смешанное произведение векторов равно нулю тогда и только тогда, когда сомножители a,b,c компланарны.
- •Смешанное произведение в ортонормированном базисе:
- •Уравнение прямой с угловым коэффициентом.
- •Общее уравнение прямой.
- •Уравнение прямой, проходящей через две заданные точки
- •Условие параллельности двух прямых.
- •Уравнение плоскости, проходящей через три различные точки, не лежащие на одной прямой:
- •Расстояние от точки до плоскости
- •Уравнение прямой, проходящей через две заданные точки
- •Взаимное расположение прямых и плоскостей в пространстве.
- •Нахождение угла между плоскостями. Косинус угла между двумя плоскостями
- •Эллипс: эллипсом называется множество точек плоскости, сумма расстояний от которых до двух данных точек, называемых фокусами эллипса, есть величина постоянная.
- •Выведение канонического уравнения эллипса:
- •Свойства определителей:
- •Умножение матриц обладает следующими свойствами:
- •Теорема о базисном миноре.
- •Ранг ступенчатой матрицы.
- •Системы линейных уравнений
- •Формулы Крамера
- •1. Пусть система имеет решение. Покажем, что .
- •Алгоритм нахождения решений произвольной системы линейных уравнений (метод Гаусса)
- •Теорема о связи решений неоднородной и соответствующей однородной слау
- •Вид общего решения неоднородной слау
1 3
Неравенство треугольника: 5
* 7
2 7
Линейная комбинация векторов: 9
Критерий линейной зависимости 2ух векторов: 9
Следствия: 10
Свойства линейно зависимых и линейно независимых векторов: 10
3 10
Критерий зависимости 2ух векторов: 10
Критерий зависимости 3ех векторов: 11
Линейная зависимость 4ех векторов: 11
4 12
5 13
6 15
7 17
Cвойства смешанного произведения: 18
Смешанное произведение векторов равно нулю тогда и только тогда, когда сомножители a,b,c компланарны. 19
Смешанное произведение в ортонормированном базисе: 19
8 19
10 21
Уравнение прямой с угловым коэффициентом. 21
Общее уравнение прямой. 22
Уравнение прямой, проходящей через две заданные точки 23
Условие параллельности двух прямых. 23
11 24
Уравнение плоскости, проходящей через три различные точки, не лежащие на одной прямой: 26
Расстояние от точки до плоскости 26
12 27
Уравнение прямой, проходящей через две заданные точки 27
13 28
Взаимное расположение прямых и плоскостей в пространстве. 28
Нахождение угла между плоскостями. Косинус угла между двумя плоскостями 28
14 30
Эллипс: эллипсом называется множество точек плоскости, сумма расстояний от которых до двух данных точек, называемых фокусами эллипса, есть величина постоянная. 30
Выведение канонического уравнения эллипса: 30
Свойства эллипса(x2/a2+y2/b2=1): 31
16 35
17 38
Свойства определителей: 39
18 42
Умножение матриц обладает следующими свойствами: 42
19 43
Теорема о базисном миноре. 46
РАНГ СТУПЕНЧАТОЙ МАТРИЦЫ. 47
20 49
Ранг и базис системы векторов 49
Определение 1. Рангом системы векторов называется максимальное число линейно независимых векторов (Система векторов называется линейно зависимой, если один из векторов системы можно представить в виде линейной комбинации остальных векторов системы, и линейно независимой - в противном случае) системы. 49
21 51
Системы линейных уравнений 51
Совместная, несовместная СЛАУ. 51
Определённая, неопределённая СЛАУ. 51
МАТРИЧНЫЕ УРАВНЕНИЯ 52
Найдем произведение 52
Формулы Крамера 52
22 54
1. Пусть система имеет решение. Покажем, что . 54
Алгоритм нахождения решений произвольной системы линейных уравнений (метод Гаусса) 55
Способ 2: Фундаментальную систему решений однородной системы можно получить и другим способом. Для этого одной переменной, перенесенной в правую часть, нужно присвоить значение 1, а остальным - нули. Вычислив значения переменных в левой части, получим одно решение из фундаментальной системы. Присвоив другой переменной в правой части значение 1, а остальным - нули, получим второе решение из фундаментальной системы и т.д. 58
23 58
24 59
25 60
Теорема о связи решений неоднородной и соответствующей однородной СЛАУ 60
Вид общего решения неоднородной СЛАУ 60
1
Скалярные
величины – записываются
числом (![]() ,m).
Векторные
– число и направление (
,m).
Векторные
– число и направление (![]() +направление).
Геометрический
вектор – направленный
прямолинейный отрезок, т.е. отрезок,
имеющий определенную длину и определенное
направление (если А-начало вектора, а
В-конец вектора, то обозначается символом
+направление).
Геометрический
вектор – направленный
прямолинейный отрезок, т.е. отрезок,
имеющий определенную длину и определенное
направление (если А-начало вектора, а
В-конец вектора, то обозначается символом
![]() ,
а
,
а
![]() - противоположный вектор =-
.
Вектор, длина которого =0, называется
нулевым вектором и обозначается
- противоположный вектор =-
.
Вектор, длина которого =0, называется
нулевым вектором и обозначается
![]() .
Нулевой вектор направления не имеет.
Векторы
.
Нулевой вектор направления не имеет.
Векторы
![]() и
и
![]() называются коллинеарными,
если они лежат на одной прямой или на
параллельных прямых, записывают
называются коллинеарными,
если они лежат на одной прямой или на
параллельных прямых, записывают
![]() .
Коллинеарные вектора могут быть
направлены одинаково или противоположно.
Нулевой вектор считается коллинеарным
любому вектору. Два вектора
и
называются
равными
(свободными) (
=
),
если они коллинеарны, одинаково направлены
и имеют одинаковые длины. Три вектора
в пространстве называются компланарными,
если они лежат в одной плоскости или в
параллельных плоскостях. Если среди
трех векторов хотя бы один нулевой или
два любые коллинеарны, то такие векторы
компаланарны. Пусть точка А-точка
приложения, т. В-т. Окончания вектора.
По типу приложения вектора делятся на:
1)свободные;
2)скользящие; 3)связанные.
Вектор называется свободным, если его
значение не меняется при произвольном
параллельном переносе. Свободным В.
является, например, скорость движения
материальной точки. В. называется
скользящим, если его значение не меняется
при любом параллельном переносе вдоль
линии его действия. Примером скользящего
В. может служить сила, действующая на
абсолютно твёрдое тело (две равные и
расположенные на одной прямой силы
оказывают на абсолютно твёрдое тело
одинаковое воздействие). В. называется
связанным, если фиксировано его начало.
Например, сила, приложенная к некоторой
точке упругого тела, представляет собой
связанный В. Вектор, длина которого
равна единице, называется единичным
вектором и обозначается
.
Коллинеарные вектора могут быть
направлены одинаково или противоположно.
Нулевой вектор считается коллинеарным
любому вектору. Два вектора
и
называются
равными
(свободными) (
=
),
если они коллинеарны, одинаково направлены
и имеют одинаковые длины. Три вектора
в пространстве называются компланарными,
если они лежат в одной плоскости или в
параллельных плоскостях. Если среди
трех векторов хотя бы один нулевой или
два любые коллинеарны, то такие векторы
компаланарны. Пусть точка А-точка
приложения, т. В-т. Окончания вектора.
По типу приложения вектора делятся на:
1)свободные;
2)скользящие; 3)связанные.
Вектор называется свободным, если его
значение не меняется при произвольном
параллельном переносе. Свободным В.
является, например, скорость движения
материальной точки. В. называется
скользящим, если его значение не меняется
при любом параллельном переносе вдоль
линии его действия. Примером скользящего
В. может служить сила, действующая на
абсолютно твёрдое тело (две равные и
расположенные на одной прямой силы
оказывают на абсолютно твёрдое тело
одинаковое воздействие). В. называется
связанным, если фиксировано его начало.
Например, сила, приложенная к некоторой
точке упругого тела, представляет собой
связанный В. Вектор, длина которого
равна единице, называется единичным
вектором и обозначается
![]() .
Единичный
вектор, направление
которого совпадает с направлением
,
называется ортом вектора
и обозначается
.
Единичный
вектор, направление
которого совпадает с направлением
,
называется ортом вектора
и обозначается
![]() .
Линейные
операции над векторами
– операции сложения и вычитания векторов,
а также умножение вектора на число:
.
Линейные
операции над векторами
– операции сложения и вычитания векторов,
а также умножение вектора на число:
1) Суммой векторов a и
b называется такой третий
вектор c, что при совмещенных началах
этих трех векторов, векторы a
и b служат сторонами
параллелограмма, а вектор c -- его
диагональю.
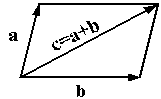
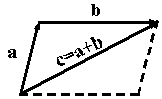 - правило треугольника
- правило треугольника
2) Разностью векторов a и b называется сумма a+(-b). Разность обозначается a-b, то есть a-b=a+(-b)
3) Произведением вектора a на
вещественное число
![]() называется
вектор b, определяемый
условием: а)
называется
вектор b, определяемый
условием: а)![]() и если
и если
![]() ,
то еще 2ум условиям: б)
коллинеарен
;
в)вектор
и
направлены одинаково, если
,
то еще 2ум условиям: б)
коллинеарен
;
в)вектор
и
направлены одинаково, если
![]() >0,
и противоположно, если
<0.
Произведение
на число
обозначается
>0,
и противоположно, если
<0.
Произведение
на число
обозначается
![]() .
.![]()
Их свойства: Для любых векторов a,b,c и любых чисел α, β:
1)a+b=b+a
(свойство коммутативности операции
сложения); 2) (a+b)+c=a+(b+c)
(свойство ассоциативности операции
сложения); 3) a+0=a;
4) a+(-a)=0; 5)
![]() (свойство ассоциативности по отношению
к числам);
(свойство ассоциативности по отношению
к числам);
6)
![]() (свойство дистрибутивности по
отношению к умножению на число); 7)
(свойство дистрибутивности по
отношению к умножению на число); 7)
![]() (свойство дистрибутивности по отношению
к умножению на вектор; 8) 1*a=a.
Очевидные свойства: 9) равенство
(свойство дистрибутивности по отношению
к умножению на вектор; 8) 1*a=a.
Очевидные свойства: 9) равенство
![]() верно
тогда и только тогда, когда или
верно
тогда и только тогда, когда или
![]() ,
или
,
или
![]() ;
10) вектор, противоположный вектору a,
равен
;
10) вектор, противоположный вектору a,
равен
![]() ,
то есть
,
то есть
![]() ;
11) для любых векторов a и b
существует такой вектор x, что
;
11) для любых векторов a и b
существует такой вектор x, что
![]()
Доказательства: Свойство 1 следует из того, что при сложении векторов по правилу параллелограмма порядок слагаемых не влияет на построение параллелограмма. Доказательство свойства 2 следует из рисунка:
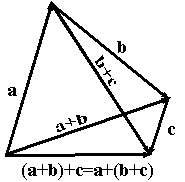
Свойства 3 и 4 очевидны при сложении векторов по правилу треугольника
Докажем свойство 5. Векторы, стоящие в
обеих частях доказываемого равенства,
имеют одинаковую длину
![]() .
Если это произведение равно нулю, то
векторы в правой и левой частях
доказываемого равенства нулевые и,
следовательно, равны друг другу. В
противном случае векторы
.
Если это произведение равно нулю, то
векторы в правой и левой частях
доказываемого равенства нулевые и,
следовательно, равны друг другу. В
противном случае векторы
![]() и
и
![]() коллинеарны
вектору а и имеют с ним одинаковое
направление, если числа
коллинеарны
вектору а и имеют с ним одинаковое
направление, если числа
![]() и
и
![]() одного
знака, и направление, противоположное
вектору а, если
и
разного знака. Следовательно,
.
одного
знака, и направление, противоположное
вектору а, если
и
разного знака. Следовательно,
.
Свойство 6 очевидно, если а=0. Если a<0 и векторы a и b неколлинеарны, то это свойство вытекает из подобия треугольников на рисунке:
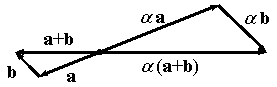
Для доказательства свойства 7 заметим,
что векторы
![]() и
и
![]() коллинеарны.
Без ограничения общности можно считать,
что
коллинеарны.
Без ограничения общности можно считать,
что
![]() (в
противном случае поменяем местами
и
(в
противном случае поменяем местами
и
![]() в
доказываемом равенстве).
в
доказываемом равенстве).
Пусть
и
одного
знака. Тогда
![]() ,
,
![]() .
.
Пусть
и
имеют
разные знаки. Тогда
![]() ,
,
![]() .
Получили, что
.
Получили, что
![]() в
обоих случаях.
в
обоих случаях.
Векторы f и g имеют одно направление.
Оно совпадает с направлением a при
![]() и
противоположно при
и
противоположно при
![]() .
Следовательно,
.
Следовательно,
![]() .
Свойство 7 доказано.
.
Свойство 7 доказано.
Свойство 8 очевидным образом вытекает из определения произведения вектора на число.
Из свойства ассоциативности (2) следует, что в сумме векторов, содержащей три и более слагаемых, можно скобки не ставить. Как найти сумму нескольких слагаемых, не используя попарных сумм, видно из рисунка:
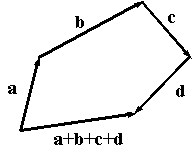
Неравенство треугольника:
Если точки А и В различны, то расстоянием между ними называется длина отрезка АВ. Если точки А и В совпадают, то расстояние между ними принимается равным нулю. Каковы бы ни были три точки, расстояние между любыми двумя из этих точек не больше суммы расстояний от них до третьей точки. Доказательство. Если две точки из трех или все три точки совпадают, то утверждение теоремы очевидно. Если все точки различны и лежат на одной прямой, то одна из них лежит между двумя другими, например В. В этом случае АВ + ВС = АС. Отсюда видно, что каждое из трех расстояний не больше суммы расстояний до двух других. Допустим, что все точки различны и не лежат на одной прямой (рис. 46). Докажем, что АВ < АС + + ВС. Опустим перпендикуляр CD на прямую АВ. По доказанному АВ < AD + BD. Так как AD < АС и BD < ВС, то АВ < АС + ВС. Теорема доказана. Заметим, что в случае, когда точки не лежат на одной прямой, в неравенстве треугольника строгое неравенство. Отсюда следует, что в любом треугольнике каждая сторона меньше суммы двух других сторон. [А] Каждая сторона треугольника меньше суммы двух других сторон.
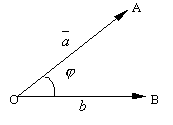
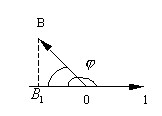
Проекция вектора на ось:
Пусть в пространстве даны два вектора
Рассмотрим ось l и отложим на ней
единичный вектор
Под углом между вектором
и
осью l понимают угол
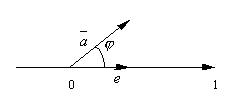
Итак, пусть l – некоторая ось и
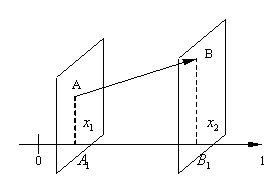
Обозначим через A1 и B1 проекции на ось lсоответственно точек A и B. Предположим, что A1 имеет координату x1, а B1 – координату x2 на оси l.
Тогда проекцией вектора
Проекцию вектора
на
ось l будем обозначать
Ясно, что если угол между вектором и осью l острый, то x2> x1, и проекция x2 – x1> 0; если этот угол тупой, то x2< x1 и проекция x2 – x1< 0. Наконец, если вектор перпендикулярен оси l, то x2= x1 и x2– x1= 0. Таким образом, проекция вектора на ось l – это длина отрезка A1B1, взятая с определённым знаком. Следовательно, проекция вектора на ось это число или скаляр. Аналогично определяется проекция одного вектора на другой. В этом случае находятся проекции концов даного вектора на ту прямую, на которой лежит 2-ой вектор. Рассмотрим некоторые основные свойства проекций. Проеция вектора на ось l равна произведению модуля вектора на косинус угла между вектором и осью:
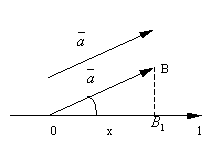
Доказательство. Ясно, что проекция
вектора не изменится при его параллельном
переносе, поэтому достаточно рассмотреть
случай, когда начало вектора совпадает
с началом отсчёта O оси l. Так
как координата проекции начала равна
нулю, то обозначим
Если угол φ острый, то из прямоугольного
Если угол φ тупой, то x< 0,
Проекция суммы двух векторов на ось
равна сумме проекций векторов на ту
же ось:
Доказательство. Пусть
Это свойство можно обобщить на случай любого числа слагаемых. Если вектор умножается на число λ, то его проекция на ось также умножается на это число:
Доказательство. Пусть угол между
вектором
и
осью
Если λ > 0, то вектор
При λ > 0
Если же λ < 0, то и имеют противоположные направления и вектор составляет с осью угол π – φ и *. Следствие. Проекция разности двух векторов на ось равна разности проекций этих векторов на ту же ось. |
|
*![]()
2
Пусть M —множество элементов произвольной природы, для которых определены операции сложения и умножения на действительное число:
паре элементов множества
![]() отвечает
элемент
отвечает
элемент
![]() ,
называемый суммой x и y;
,
называемый суммой x и y;
паре
![]() ,
,
![]() —
любое действительное число, отвечает
элемент
—
любое действительное число, отвечает
элемент
![]() ,
называемый произведением числа
и
элемента x.
,
называемый произведением числа
и
элемента x.
Будем называть множество M линейным
пространством, если для всех его
элементов определены операции сложения
и умножения на действительное число и
для любых элементов
![]() и
произвольных чисел
и
произвольных чисел
![]() справедливо:
справедливо:
1)![]() ,
сложение коммутативно; 2)
,
сложение коммутативно; 2)![]() ,
сложение ассоциативно; 3)существует
единственный нулевой элемент
,
сложение ассоциативно; 3)существует
единственный нулевой элемент
![]() такой,
что
такой,
что
![]() ;
4)для каждого элемента существует
единственный противоположный элемент
-x такой, что
;
4)для каждого элемента существует
единственный противоположный элемент
-x такой, что
![]() ,
5)
,
5)![]() ,
умножение на число ассоциативно; 6)
,
умножение на число ассоциативно; 6)![]() ;
7)
;
7)![]() ,
умножение на число дистрибутивно
относительно сложения элементов; 8)
,
умножение на число дистрибутивно
относительно сложения элементов; 8)![]() ,
умножение элемента на число дистрибутивно
относительно сложения чисел.
,
умножение элемента на число дистрибутивно
относительно сложения чисел.
Равенства 1—8 называют аксиомами линейного пространства.
Линейное пространство часто называют векторным пространством, а его элементы — векторами.
Следствия из аксиом линейного пространства:
В линейном пространстве существует единственный нулевой вектор;
В линейном пространстве у каждого вектора существует единственный противоположный вектор;
x X 0 K x = θ ;
α R α K θ = θ ;
x X −x = (−1) K x ;
Если α K x = θ , то либо α = 0 , либо x = θ .
Примерами вещественных линейных пространств могут служить:
множество столбцов
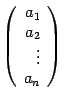 из
из
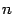 элементов,
являющихся вещественными числами;
элементов,
являющихся вещественными числами;
множество многочленов степени не выше с вещественными коэффициентами;
множество всех многочленов с вещественными коэффициентами;
множество функций непрерывных на некотором отрезке
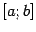 .
.
В примерах 2-4 нулевым вектором является многочлен или функция тождественно равная нулю, то есть равная нулю при всех значениях аргумента. Проверку того, что указанные множества являются линейными пространствами, предоставляем читателю.
Арифметическим
вектором называется
упорядоченная совокупность n чисел.
Обозначается
![]() ,
числа
,
числа
![]() называются
компонентами арифметического вектора.
называются
компонентами арифметического вектора.
Для арифметических векторов определены
линейные операции — сложение арифметических
векторов и умножение вектора на число:
![]() ,
,
для любых
![]() и
и
![]() и
любого числа
и
любого числа
![]()
Определение. Множество арифметических векторов, для которых определены операции сложения и умножения на число называется пространством арифметических векторов Rn.
Вектор
![]() называется
нулевым вектором, а вектор
называется
нулевым вектором, а вектор
![]() —
противоположным вектором для вектора
.
—
противоположным вектором для вектора
.
Для любых
,
,
![]() из
Rn и любых чисел ,
справедливо:
из
Rn и любых чисел ,
справедливо:
![]() ,
сложение коммутативно;
,
сложение коммутативно;
![]() ,сложение
ассоциативно;
,сложение
ассоциативно;
![]()
![]()
![]() ,
умножение на число ассоциативно;
,
умножение на число ассоциативно;
![]() ;
;
![]() ,
умножение на число дистрибутивно
относительно сложения элементов;
,
умножение на число дистрибутивно
относительно сложения элементов;
![]() ,
умножение вектора на число дистрибутивно
относительно сложения чисел.
,
умножение вектора на число дистрибутивно
относительно сложения чисел.
Примерами пространства арифметических векторов являются пространства геометрических векторов на плоскости, записанных в координатной форме.
Пространство матриц Mmxn включает в себя мн-во матриц размера mxn.Пространство Mmxn линейно т.к. для него выполняются все пункты определения линейного пространства.
Пусть L-множество всех многочленов от одной переменной, степень которых не выше заданного числа n.Сумма двух многочленов есть также многочлен степенью не выше n.
Произведение многочлена из L на число эL есть также многочлен степенью не выше n.
Легко проверить что аксиомы линейного пространства выполняются. Роль нуля играет многочлен все коэффициенты которого равны нулю.
Рассмотрим множество всех функций от одной независимой переменной а, определенных и непрерывных для 0<=a<=1.Любым функциям f(a) и g(a) из этого множества можно составить их сумму в обычном смысле слова f(a)+g(a),которая будет также определена и непрерывна для 0<=a<=1 и, следовательно, будет принадлежать рассматриваемому множеству. Числу L и функции f(a) сопоставляется функция Lf(a),которая определена и непрерывна для 0<=a<=1,если этим свойством обладает f(a) все 8 аксиом выполнены. Роль нуля играет функция тождественно равная нулю.

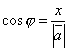 .
Откуда
.
Откуда
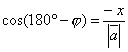 .
Т.е.
.
Т.е.
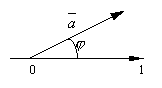 .
.