Вариант № 4
Принять решение по поводу покупки оборудования за 18 000 у. е., если в будущем оно будет генерировать доход, характеризующийся следующим потоком: 1 год – 10 000 у. е., 2 год – 5 000 у. е., 3 год – 6 000 у.е. Альтернативная доходность 8 % годовых.
1 год:
2 год:
3 год:
Общий доход за 3 года: 18308,91
18309-18000=309 у.е. – доход за три года превышает стоимость покупки оборудования, следовательно, покупка целесообразна.
Вариант № 5
Банк принимает вклады на срочный депозит на следующих условиях:
Срок 35 дней – 8% годовых
Срок 65 дней – 10,5% годовых
Срок 90 дней – 11,5% годовых
Срок 120 дней – 13,5% годовых
Срок 180 дней – 15% годовых
Рассчитать доход клиента при вкладе 50000 руб. на указанные сроки (год високосный).
Решение
=
;
;
.
;
;
.
;
;
.
;
;
.
;
;
.
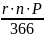
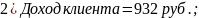
Вариант № 6
Строительство жилого дома сегодня обходится 800 млн. руб. В связи с инфляцией оно будет дорожать на 10% ежегодно. Какую сумму необходимо внести на депозит, чтобы профинансировать строительство через 5 лет, если доходность по банковским операциям 8% в год?
Решение:
1)
млн. руб.
2)
млн. руб.
Ответ: 877,064 млн. руб.
Решение 2:
FV=PV(1+r)n
FV=800(1+0,1)5=1288,4 млн. руб.
1288,4=PV(1+0,8)5
PV=
= 876,7 млн. руб.
Ответ: 876,7 млн. руб.
Вариант № 7
ООО «Маяк» решило взять кредит на сумму 10000 рублей на 6 месяцев. Банк «А» предлагает кредит с ежемесячным погашением равными долями при ставке 60% годовых. Банк «Б» предлагает такой же кредит, но с разовым погашением по окончании срока кредита, ставка за пользование кредитом 55% годовых. Определите, какой кредит выгоднее ООО «Маяк»?
Решение.
Размер разового погашения кредита (ежемесячного аннуитетного платежа) в банке «А»:
где S – сумма кредита;
r – месячная процентная ставка;
n – количество полных процентных периодов, оставшихся до возврата.
Месячная процентная ставка составит:
где r(год.)-годовая процентная ставка.
Полная сумма выплат за кредит С составит:
Стоимость кредита равна: 11820 – 10000 = 1820 руб.
Размер выплат при погашении кредита в банке «Б» составит:
,
где S – наращенная сумма;
PV – сумма выданного кредита;
r – процентная ставка;
n – срок ссуды, в месяцах.
Стоимость кредита равна: 12750 – 10000 = 2750 руб.
1820<2750
Вывод: Кредит в банке «А» выгоднее.
Вариант № 8
Господином П. были отданы 3400 рублей под 5% (простых) некоторой коммерческой фирме, а 3250 рублей он положил в банк, выплачивающий 6%. Через сколько лет обе суммы превратятся вместе с процентными деньгами в одну и туже величину? Проценты в обоих случаях простые.
Решение
Решение:
,
r – требуемый уровень доходности (%);
n – продолжительность процесса инвестирования (год).
Ответ: через 6 лет обе суммы превратятся вместе с процентными деньгами в одну и ту же величину.
Вариант № 9
Рыночная стоимость облигации 8500 руб. Эмитент гарантирует выплату 10% ежеквартального купонного дохода и погашение облигации через 3 года. Стоит ли приобретать облигацию, если ее номинал 9000 руб., а доходность по банковскому вкладу 12% годовых?
Решение
1)Будущая сумма денежного потока при покупке облигации:
FV=С(1+r)n
Где С- рыночная стоимость облигации;
n- количество лет;
r- купонная ставка.
FV=9000(1+0,1/4)3*4=12104руб.
2)Будущая сумма при размещении на депозит в банке:
FV=C(1+r)n
FV=8500(1+0,12)3=11941,89руб.
12104>11941,89
Ответ: стоит приобретать облигацию.
Вариант № 10
Создается фонд путем ежегодных взносов по 5 млн. руб. с гарантированной доходностью 10% в год. Определить величину фонда к концу 5-го года, если величина первоначального взноса 40 млн. руб.
Решение
FV=С1*((1+r)n-1)/r+C2*(1+r)n , где
FV – будущая величина фонда,
C1 – величина аннуитетных платежей за 1 период,
C2 – величина первоначального взноса,
r – ставка процента,
n – количество периодов.
FV=(5000000/0,1)*((1+0,1)5-1)+40000000*(1+0,1)5=94925500руб.
Ответ: 94 млн 925,5 тыс. руб.
Решение 2
1) Определяем будущую стоимость аннуитета постнумерандо:
FV.
=C∙
,
где C – величина годового платежа, млн. руб.
–коэффициент наращения аннуитета.
FV.
=5∙
,
2) Определяем будущую стоимость первоначального взноса:
FV= PV∙(1+r)n,
Где r – ставка дисконта, %
n- продолжительность процесса инвестиций, год
FV= 40∙(1+0,1)5 =64,42 млн. руб
2) Определяем величину фонда к концу 5-го года:
64,42+30,53=94,95 млн. руб.
Ответ: Величина фонда к концу 5-го года будет равна 94,95 млн. руб.