Все формулы

Естественным способом сравнивать денежные потоки в разные сроки в разные сроки является их приведение к одному и тому же моменту времени. Как правило, в качестве такого момента выбирают или момент начала инвестиций, или момент в будущем. Если денежный поток приводят к нулевому моменту, такой процесс называют дисконтированием. Величину денежных средств в момент инвестирования называют текущей стоимостью (PV). Если денежный поток приводят к моменту в будущем, то такой процесс называют наращением стоимости. Стоимость в будущем инвестированных сегодня денежных средств называют будущей стоимостью (FV).

Наращение:

Простые проценты (Когда доход от вклада должен периодически выплачиваться заемщиком и тут же изыматься кредитором)

R - выбранная ставка дисконта, процент (требуемый уровень доходности от инвестиций аналогичного содержания и степени риска)

N - продолжительность процесса инвестиций, лет

Сложные проценты

Сравнение формул 1 и 2 показывает, что доход при простой процентной ставке меняется по линейному закону, а при сложной процентной ставке - по закону экспоненты.

В связи с тем, что схема сложного процента подвергает кредитора большему риску, он должен получать и большее вознаграждение.

При расчетах кредитных операций более года используется сложная процентная ставка, до года - простая.

Если число лет не целое, то n может быть выражена в днях:

D-число дней, T - дней в году

Проценты могут начисляться несколько раз в году. Дополнительно указывают, сколько раз в году происходит начисление процентов (m - число начислений процентов в году).

Для простых процентов:

Для сложных процентов:

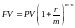
Практика 2. Если задана исходная сумма PV, годовая процентная ставка r и число начислений сложных процентов m, этому набору исходных величин в рамках одного года соответствует вполне определенное значение наращенной величины FV. Требуется найти такую годовую ставку rэффективное, которая обеспечила бы точно такое же наращение, как и исходная схема, но при однократном начислении процентов

Дисконтирование – обратная величина наращению, то есть процесс приведения будущей суммы денег к современной стоимости.

- простые проценты; - сложные проценты

Система	Число дней в месяце, d		Число дней в году	День приема(выдачи) вклада
Система	Неполный месяц	Полный месяц	Число дней в году	День приема(выдачи) вклада
Германия	Факт	30	360	-1
Англия	Факт	Факт	Факт	-1
Франция	Факт	Факт	360	-1

Формула позволяет найти только проценты:

n – срок, r – ставка, P – сумма

Если за стартовыми (первоначальными) инвестициями следует несколько равных платежей от реализации проекта, то денежный поток из периодических платежей одинаковой величины, возникающих через равные промежутки времени, называется аннуитетным.

По моменту выплаты в пределах периода между платежами ренты: