
- •1 1 . Системы сбора и обработки данных, основные определения, разновидности. Задачи, решаемые разновидностями систем.
- •1.Производство
- •1.Производство
- •1.Экспериментальное исследование объектов, процессов или явлений
- •2 2 . Классификация измерительных систем. Функции, выполняемые в измерительных системах. Характеристики измерительных систем.
- •3 3 . Точностные характеристики измерительных систем.
- •4 4 . Быстродействие измерительных систем. Квантование во времени и восстановление сигнала. Погрешности восстановления.
- •5 5 . Обобщенная структурная схема ис. Основные функциональные блоки и типовые структуры. Сравнение характеристик различных структур измерительных систем.
- •6 6 . Помехоустойчивость измерительных систем. Источники и разновидности помех.
- •7 7 . Влияние заземления, внутреннего сопротивления источника и приемника на помехоустойчивость. Методы повышения помехоустойчивости.
- •8 8 . Теплоизмерительная система «Тепло-2». Структурная схема, общая характеристика. Первичные измерительные преобразователи и каналы измерения.
- •9 9 . Алгоритмы повышения точности измерений в «Тепло-2».
- •1 10 0. Контроль – основные определения и задачи. Классификация систем контроля
- •1 11 1. Системы контроля. Структуры и разновидности каналов контроля.
- •1 13 3. Полнота контроля. Способы оценки полноты контроля.
- •1 14 4. Достоверность контроля. Ошибки контроля, природа возникновения ошибок.
- •1 15 16 5. 16. Оценка ошибки контроля 1-го и 2-го рода.
- •1 18 8. Эффективность контроля, способы оценки эффективности.
- •1 19 9. Пpедмет и задачи технической диагностики. Основные опpеделения.
- •2 20 0. Виды ошибок и неиспpавностей. Модели объектов диагностиpования.
- •2 21 1. Таблица функций неиспpавностей. Совокупности обнаpуживающих и pазличающих пpовеpок.
- •2 22 2. Синтез теста контроля по таблице функций неисправностей.
- •2 23 3. Синтез диагностического теста по таблице функций неисправностей.
- •2 24 4. Оптимизация тестов.
- •2 25 5. Хаpактеpистики систем диагностирования.
- •2 290 9. Постpоение тестов методом pазличающих функций
- •30. Постpоение тестов методом существенных путей
- •Построение тестов методом существенных путей
- •3 31 1. Модели автоматов с памятью. Особенности диагностиpования автоматов с памятью.
- •3 32 2. Пpоблемы испытаний микpопpоцессоpных систем. Методы испытаний.
- •3 33 3. Анализ логических состояний. Устpойство и пpинцип действия анализатоpов логических состояний
- •3 34 4. Устройство и принцип действия сигнатурного анализатора.
- •3 35 5. Алгоритм поиска неисправностей с помощью сигнатурного анализатора.
- •1. Системы сбора и обработки данных, основные определения, разновидности. Задачи, решаемые разновидностями систем.
- •2. Классификация измерительных систем. Функции, выполняемые в измерительных системах. Характеристики измерительных систем.
30. Постpоение тестов методом существенных путей
Метод существенных путей Для того, чтобы неисправность была обнаружена на внешнем выходе объекта, необходимо и достаточно, чтобы 1.неисправность проявилась в каком- нибудь внутреннем узле объекта и 2. существовал путь для транспортировки сигнала о неисправности с этого внутреннего узла до какого-нибудь внешнего выхода объекта
Пусть ОД содержит:
- N логических элементов - n входных
полюсов - k выходных полюсов каждый i-тый
логический элемент объекта (1 i
N): - имеет ni входов (1
m
ni ) - на каждом входе
реализуется функция yim -
на выходе реализуется функция yi
i
N): - имеет ni входов (1
m
ni ) - на каждом входе
реализуется функция yim -
на выходе реализуется функция yi
Для i-того логического элемента задан список из Si логических неисправностей. Функцию, реализуемую элементом с неисправностью s, (1 s Si ), обозначим ysi
Неисправность s проявится на выходе элемента i, если найдется набор входных функций
Yi
(0,s) = { yi1 , yi2,…,
yim , yini }
такой, что выходные функции элемента с
неисправностью и без неисправности не
совпадут ysi (Yi)
 y0i (Yi)
(1) Выразив входные функции yim
i-того элемента через входные (для
объекта) переменные x1 ,
x2 ,…, xn , можно
найти наборы входных переменных,
удовлетворяющих (1).
y0i (Yi)
(1) Выразив входные функции yim
i-того элемента через входные (для
объекта) переменные x1 ,
x2 ,…, xn , можно
найти наборы входных переменных,
удовлетворяющих (1).
Для этого можно
воспользоваться различающей функцией
для выходной функции y i элемента: D[ ysi
, y0i] Истинность
этой различающей функции и есть условие
проявления неисправности на выходе
элемента

Условие проявления неисправности на выходе элемента является необходимым, но недостаточным условием обнаружения неисправности на выходе объекта. Должно быть также выполнено и условие транспортировки неисправности.
Условием
транспортировки
 неисправности
s от выхода элемента
i до внешнего выхода
неисправности
s от выхода элемента
i до внешнего выхода
 объекта
является наличие существенного пути
между этими полюсами. Транспортировка
от полюса i до выхода
обеспечивается при истинности логической
функции от входных переменных:
объекта
является наличие существенного пути
между этими полюсами. Транспортировка
от полюса i до выхода
обеспечивается при истинности логической
функции от входных переменных:

Если в объекте
k выходов, то условие
транспортировки есть дизъюнкция
![]() Решение этого уравнения дает все наборы
входных переменных
Решение этого уравнения дает все наборы
входных переменных
Xj =[x1, x2,…, xn], при которых неисправность транспортируется на выход объекта.
Как найти ? 1. Условно отключим выход i-того элемента от входов остальных элементов логической сети, связанных с полюсом i 2. Образовавшийся полюс сопоставим с дополнительной «входной» переменной yi 3. Найдем набор входных переменных
Xj
=[x1, x2,…,
xn],
при котором изменение дополнительной
переменной yi
будет замечено на каком-либо внешнем
выходе
объекта, т.е. при котором изменение
значения yi
приводит к изменению значения выходной
функции
 .
Такие наборы являются рабочими наборами
булевой производной функции
.
Такие наборы являются рабочими наборами
булевой производной функции
 по переменной yi
.
по переменной yi
.
![]()
А булева производная функции по переменной yi и есть условие транспортировки

(Булева производная совпадает с различающей функцией, если неисправность заключается в инвертировании переменной yi )
 производная от инверсии функции равна
производной от функции
производная от инверсии функции равна
производной от функции производная по инверсии переменной
равна производной от переменной
производная по инверсии переменной
равна производной от переменной производная равна нулю, если функция
не зависит от переменной, т.е. если
производная равна нулю, если функция
не зависит от переменной, т.е. если

 производная равна единице, если функция
зависит только от переменной, по которой
берется производная
производная равна единице, если функция
зависит только от переменной, по которой
берется производнаяпроизводная от конъюнкции функций
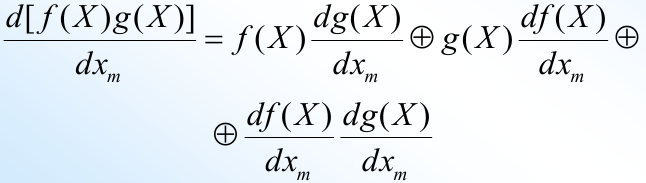
производная от дизъюнкции функций

