Критерий устойчивости Раусса-Гурвица

Математики Раусс (Англия) и Гурвиц (Швейцария) разработали этот критерий приблизительно в одно время. Отличие заключалось в алгоритме вычислений. Мы познакомимся с критерием в формулировке Гурвица.

По Гурвицу для устойчивости необходимо и достаточно, что­бы при a₀ > 0 определитель Гурвица  = _n и все его главные миноры ₁, ₂,..., _n-1 были строго положительны, т.е.

(2.9.4)

Cтруктура определителя Гурвица легко запоминается, если учесть, что по главной диагонали расположены коэффициенты а₁,…,а_n, в строчках расположены коэффициенты через один, если они исчерпаны, то свободные места заполняются нулями.

Необходимость условия устойчивости по критерию Гурвица. Необходимость заключается в том, что, если система устойчивая, то все определители Гурвица будут строго положительными, что говорит о том, что система будет устойчивой.

Достаточность условия устойчивости по критерию Гурвица. Достаточность заключается в том, что наличие всех положительных определителей Гурвица в матрице гарантирует устойчивость, что не сложно проверить на примере.

Пример 2.9.2. Исследовать на устойчивость по Гурвицу систему с единичной отрицательной обратной связью, в прямой цепи которой включены три инерционных звена и, следовательно, передаточная функция разомкнутой системы имеет вид (2.9.5)

Запишем характеристическое уравнение замкнутой системы как сумму числителя и знаменателя (2.9.5):

Следовательно,

Определитель Гурвица и его миноры имеют вид

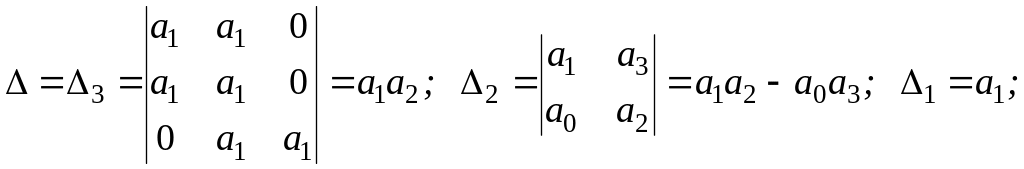(2.9.6)

с учетом a₀ > 0 из строгой положительности определителя Гурвица и миноров (2.9.6) вытекает условие Стодолы и, кроме того, условие a₁ a₂ - a₀ a₃ > 0, что после подстановки значений коэффициентов дает

(Т₁Т₂+ Т₁Т₃+Т₂Т₃)(Т₁+Т₂+Т₃)>Т₁Т₂Т₃(1+k). (2.9.7)

Отсюда видно, что при увеличении k система из устойчивой может превратиться в неустойчивую, так как неравенство (2.9.7) переста­нет выполняться.

Передаточная функция системы по ошибке равна

(2.9.8)

Согласно теореме о конечном значении оригинала установившаяся ошибка отработки единичного ступенчатого сигнала будет равна 1/(1+k). Следовательно, обнаруживается противоречие между ус­тойчивостью и точностью. Для уменьшения ошибки надо увеличивать k, но это приводит к потере устойчивости.

Принцип аргумента и критерий устойчивости Михайлова

Критерий Михайлова основан на так называемом принципе аргумента.

Рассмотрим характеристический полином замкнутой системы, который по теореме Безу можно представить в виде

D(p) = a₀pⁿ+ a₁p^n-1+…+ a_n = a₀(p - p₁)…(p - p_n).

Сделаем подстановку p = j

D(j) = a₀(j)ⁿ+ a₁(j)^n-1+…+ a_n = a₀(j - p₁)…(j - p_n) = X()+jY().

Для конкретного значения  имеет точку на комплексной плоскости, задаваемую параметрическими уравнениями

Е сли изменять  в диапазоне от - до , то будет прочерчена кривая Михайлова, т. е. годограф. Изучим поворот вектора D(j) при изменении  от - до , т. е. найдем приращение аргумента вектора (аргумент равен сумме для произведения векторов): .

При  = -  разностный вектор, начало которого в точке р_i, а конец на мнимой оси, направлен вертикально вниз. По мере роста  конец вектора скользит вдоль мнимой оси, а при  =  вектор направлен вертикально вверх. Если корень левый (рис. 2.9.19а), то  arg = +, а если корень правый, то  arg = -.

Если характеристическое уравнение имеет m правых корней (соответственно n - m левых), то .

Это и есть принцип аргумента. При выделении действительной части Х() и мнимой Y() мы отнесли к Х() все слагаемые, содержащие j в четной степени, а к Y() – в нечетной степени. Поэтому кривая Михайлова симметрична относительно действительной оси (Х() – четная, Y() – нечетная функция). В результате, если изменять  от 0 до +, то приращение аргумента будет в два раза меньше. В связи с этим окончательно принцип аргумента формулируется следующим образом 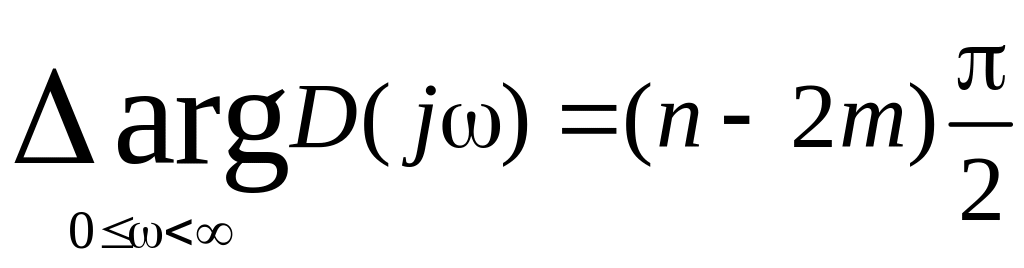. (2.9.29)

Если система устойчива, т.е. m = 0, то получаем критерий устойчивости Михайлова.

По Михайлову для устойчивости необходимо и достаточно, чтобы

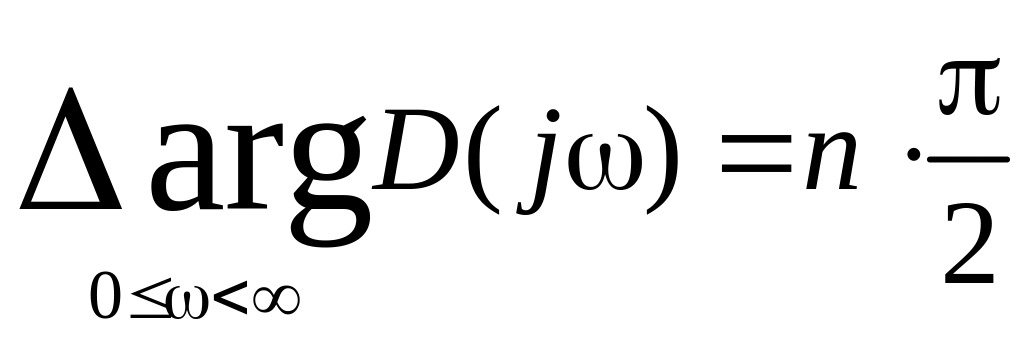, (2.9.30)

то есть кривая Михайлова должна последовательно проходить через n четвертей против часовой стрелки.

Очевидно, что для применения критерия Михайлова не требуется точного и детального построения кривой. Важно установить, каким образом она огибает начало координат и не нарушается ли последовательность прохождения n четвертей против часовой стрелки.

Необходимость условия устойчивости по критерию Михайлова. Необходимость заключается в том, что, если система устойчивая, то приращение аргумента вектора будет равным согласно формуле (2.9.30), что говорит о том, что система будет устойчивой.

Достаточность условия устойчивости по критерию Михайлова. Достаточность заключается в том, что приращение аргумента вектора гарантирует устойчивость, что не сложно проверить на примере.

Пример 2.9.6. Применить критерий Михайлова для проверки устойчи­вости системы, показанной на рис.2.9.20.

Характеристический полином замкнутой системы при k₁k₂ > 0 соответствует устойчивой системе, так условие Сто­долы выполняется, а для n = 1 оно достаточно. Можно непосред­ственно найти корень р₁ = - k₁k₂ и убедиться, что необходимое и достаточное условие устойчивости выполнено. Поэтому применение критерия Михайлова носит иллюстративный характер. Полагая p=j, получим

D(j) = X()+jY(),

где Х() = ; Y() =  . (2.9.31)

По параметрическим уравнениям (2.9.31) построен годограф Ми­хайлова на рис.2.9.21, из которого видно, что при изменении  от 0 до  вектор D(j) поворачивается против часовой стрел­ки на +/2 , т.е. система устойчива.