Методические указания

Парная регрессия представляет собой модель, где среднее значение зависимой переменной y рассматривается как функция одной независимой переменной (регрессора) x; уравнение парной регрессии имеет вид

В зависимости от характера парной регрессии различают:

– прямую регрессию (увеличение объясняющей переменной вызывает увеличение зависимой переменной);

– обратную регрессию (увеличение объясняющей переменной вызывает уменьшение зависимой переменной).

В случае парной модели для ее спецификации используется графический метод. Он заключается в построении корреляционного поля (или диаграммы рассеивания), которое позволяет произвести визуальный анализ эмпирических данных. По ширине разброса точек можно сделать вывод о степени тесноты связи.

Для определения характера парной регрессии может быть использована выборочная ковариация :

– при связь между факторами прямая;

– при связь между факторами обратная.

При определении оценок параметров нелинейных моделей парной регрессии применяют процедуру линеаризации. Она состоит в том, что с помощью преобразований переменных от каждого из уравнений переходят к рассмотрению соответствующего линейного уравнения относительно новых переменных. В таблице приведены виды регрессий и формулы оценок параметров.

Оценки параметров нелинейных моделей регрессии

Вид регрессии	Линеаризующее преобразование	Параметры уравнения регрессии
Экспоненциальная регрессия
Логарифмическая регрессия
Степенная регрессия		,
Показательная регрессия
Гиперболическая регрессия

Степень взаимосвязи результативного признака с фактором в случае нелинейной парной регрессии оценивает индекс корреляции ( ):

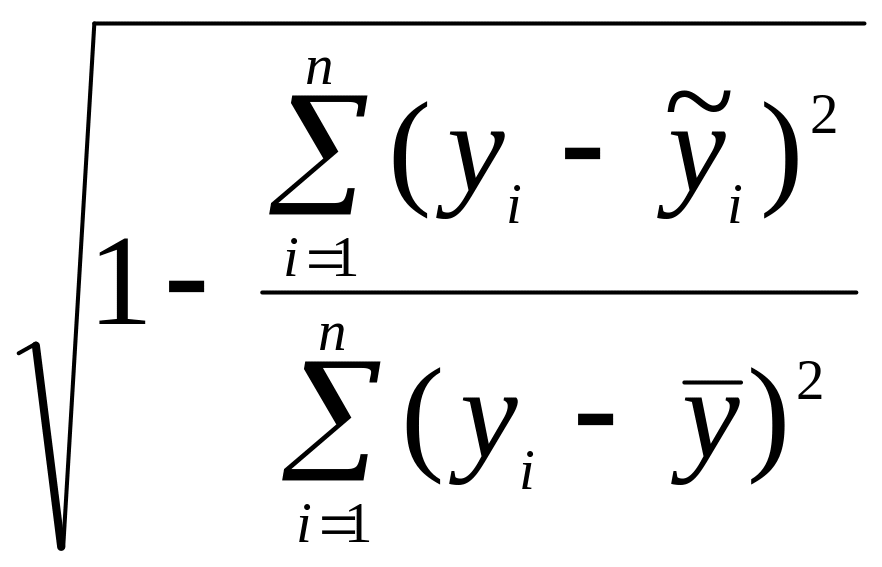
Чем ближе к единице, тем теснее связь рассматриваемых признаков.

Для анализа общего качества уравнения нелинейной парной регрессии обычно используется индекс детерминации . Он определяют долю разброса результативного признака, обусловленную изменением факторного признака. Величина показывает в процентах, какая часть изменения зависимой переменной y определяется объясняющей переменной x, а какая – другими случайными факторами.

Для оценки адекватности уравнения регрессии используется показатель средней ошибки аппроксимации:

– среднее отклонение расчетных значений от фактических, допустимый предел которого не более 8 – 12 %.

Средний коэффициент эластичности на основании вида уравнения парной регрессии позволяет определить, на сколько процентов в среднем по совокупности изменится результирующий фактор y при изменении фактора x на 1 % от своего номинального значения. Частное значение коэффициента эластичности при заданном значении независимого фактора определяется путем подстановки в уравнение значения .

Точечный прогноз результирующего признака y при заданном значении независимого фактора определяется путем подстановки в уравнение регрессии значения .