
- •1.Предмет статистики. Направления развития статистики. Организация статистики в России.
- •2.Статистическая совокупность и ее характеристика. Закон больших чисел.
- •Особенности предмета статистической науки.
- •9) Способы статистического наблюдения: непосредственное, документальное, опрос. Способы получения статистической информации:
- •Вопрос 10. Программно–методологические вопросы статистического наблюдения
- •Вопрос 12. Понятие и виды статистической сводки: простая и сложная
- •Вопрос 14
- •15. Статистические распределения и их основные характеристики. Графическое представление рядов распределения: полигон, гистограмма, кумулята.
- •17 )Графическое изображение статистических данных. Классификация видов графиков. Диаграммы сравнения. Структурные диаграммы. Диаграммы динамики. Статистические карты.
- •Классификация видов графиков.
- •18) Понятие, виды и значение статистических показателей. Функции статистических показателей.
- •19. Абсолютные величины, их основные виды.
- •20. Относительные величины
- •21.Сущность и значение средних показателей. Виды средних и методы их расчета. Свойства средней арифметической.
- •22. Структурные средние величины: мода и медиана
- •23. Вариация признака в совокупности и ее значение. Абсолютные и средние показатели вариации и способы их расчета(размах вариации, среднее линейное отклонение, дисперсия, коэффициент вариации)
- •24.Виды дисперсий в совокупности, разделенной на группы (общая дисперсия,межгрупповая, средняя из внутригрупповых) Правило сложения дисперсий. Эмпирическое корреляционное отношение.
- •25.Теоретические основы выборочного метода
- •26. Методы отбора единиц в выборочную совокупность.
- •28) Определение оптимальной численности выборки
- •29. Понятие о рядах динамики. Элементы динамического ряда. Виды рядов динамики.
- •30. Сопоставимость уровней ряда динамики.
- •Вопрос 49.Показатели использования рабочего времени. Фонды рабочего времени. Основные показатели и методы расчета производительности труда.
- •50. Уровень жизни населения. Доходы населения
- •Вопрос 53
- •Показатели движения основных фондов
26. Методы отбора единиц в выборочную совокупность.
Существует три основных способа отбора единиц совокупности при выборочном наблюдении: случайный, механический и типический.
Случайный отбор, когда обследуемые единицы отбираются из всей совокупности наугад, т.е. каждая единица имеет совершенно одинаковые шансы попасть в выборку (например, с помощью жребия, жетонов).
Механический отбор - это отбор каждой 5-ой, 10-ой, 20-ой и т.д. единицы совокупности. Например, из 600 уголовных дел о краже (генеральная совокупность), решено подвергнуть выборочному наблюдению 120 дел (объем выборки), разделив 600 на 120, получаем 5. Это значит, что отбирая механически каждое 5 дело, можно получить выборку, свободную от субъективного влияния исследователя.
Типический (типичный) отбор заключается в том, что генеральная совокупность сначала расчленяется на однородные (типичные) группы, из которых затем производится пропорциональный отбор, например, каждой пятой, восьмой, десятой и т.д. части каждой группы. Полученная таким образом выборочная совокупность представляет собой как бы уменьшенную модель генеральной совокупности с сохранением всех ее основных свойств и признаков.
4. Серийная. Отбирают не отдельные единицы, а целые группы или серии. Затем обследуют все единицы отобранных групп. Способ отбора случайный, либо механический, но бесповторным способом.
5. Многоступенчатая выборка. Типически отобранная часть сочетается с несколькими стадиями или ступенями отбора, причем на каждой ступени выбирается своя единица.
6. Многоразовая. Сохраняется одна и та же единица совокупности.
7. Комбинированная. Выборочное наблюдение сочетается со сплошным.
8. Моментное наблюдение. Фиксируются не единицы совокупности, а состояние явления.
9. Малая выборка. Число единиц до 20.
27)
Способы (виды) выборки: собственно-случайная, механическая(систематическая),типическая(стратификационная),серийная выборка.
Собственно случайная выборка формируется в строгом соответствии с научными принципами и правилами случайного отбора. Для получения собственно случайной выборки генеральная совокупность строго подразделяется на единицы отбора, и затем в случайном повторном или бесповторном порядке отбирается достаточное число единиц.
При повторном отборе При безповторном отборе
 (ср.кол-го
признака)
(ср.кол-го
признака)
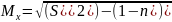 (ср.кол-го признака)
(ср.кол-го признака)
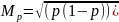 (альтер-го
признака)
(альтер-го
признака)
 (альтер-го
признака)
(альтер-го
признака)
Механическая выборка – отбор единиц выборной совокупности из генеральной совокупности(Г.С), разбитой по нейтральному признаку на равные интервалы или группы. Из каждой группы выбирается 1 единица, чтобы избежать ошибки единица находится в середине группы.
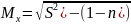

Для отбора единиц из однородной совокупности применяется типическая выборка. При условии когда единицу Г.С. можно разбить на несколько качественно однородных, однотипных групп по признакам, влияющим на изучаемые показатели.
Для средней количественного признака
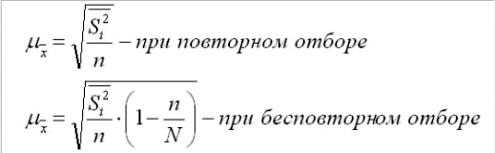
Где S-среднее из внутригрупповых дисперсий по выборочной совокупности
Для альтернативного признака:
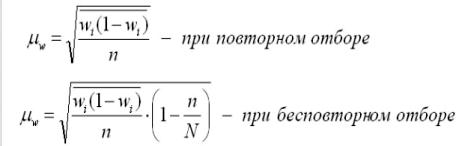
Где w(1-w) –средняя из внутригрупповых дисперсий доли (альтернативного признака) по выборочной совокупности.
Серийная выборка – предполагает случайный отбор из генеральной совокупности не отдельных единиц, а равновесных групп, с тем чтобы в таких группах подвергать наблюдению все единицы.
Для средней количественного признака
 где
r-
число отобранных серий, R-общее
число серий, дельта-квадрат – межгрупповая
дисперсия серийной выборки, рассчитанная
по формуле
где
r-
число отобранных серий, R-общее
число серий, дельта-квадрат – межгрупповая
дисперсия серийной выборки, рассчитанная
по формуле
![]() где xi
средняя
i-й
серии, х-ошибка средняя по всей выборочной
совокупности
где xi
средняя
i-й
серии, х-ошибка средняя по всей выборочной
совокупности
Для альтернативного признака
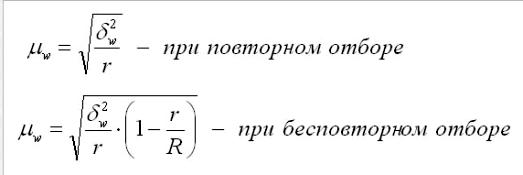 межгрупповая
дисперсия доли серийной выборки
определяется
межгрупповая
дисперсия доли серийной выборки
определяется![]() где
wi
- средняя i-й
серии, w-ошибка
средняя по всей выборочной совокупности
где
wi
- средняя i-й
серии, w-ошибка
средняя по всей выборочной совокупности
