3.7. Производственные функции

Одной из важнейших характеристик, определяющих возможности предприятия, в том числе и учебного заведения, является его производственная функция.

Под производственной функцией в дальнейшем подразумевается зависимость между количеством произведенной продукции заданного качества и средствами, затраченными на ее изготовление.

Она определяется как эндогенными, так и экзогенными факторами, управляющими производственным процессом.

К эндогенным факторам относятся: оснащенность основным оборудованием и организация производственного процесса, а также обеспеченность обучающим персоналом.

К экзогенным - потребность в выпускаемой продукции.

Поскольку речь идет о создании единой системы образования, необходимо заботиться не только о качестве подготовки специалистов, но и об экономической эффективности создаваемой системы. Поэтому мы должны ввести в математическую модель параметры, позволяющие учесть экономические факторы.

Пока рассматривается учебное заведение, подготавливающее специалистов одной профессии и квалификации.

В экономике весьма часто зависимость между стоимостью продукции и ценой затраченного обобщенного ресурса выражается зависимостью

, (3.8)

где - текущая стоимость продукции; - цена ресурса; -постоянные коэффициенты.

Применительно к учебному заведению под стоимостью продукции будем подразумевать стоимость труда, который может произвести выпускник данного учебного заведения.

График функции 3.8 представлен на рис.3.4 (кривая I) где - стоимость минимального количества продукции, выпускаемого учебным заведением в начальной стадии подготовки специалистов; - стоимость продукции на стадии, когда завершился пусковой режим и учебное заведение начинает стабильно функционировать; - стоимость продукции, когда учебное заведение работает в оптимальном режиме; - стоимость продукции в режиме максимального перегруза, когда рентабельность учебного заведения в результате нарушения технологии делается равной нулю.

Соответствующие значения цены ресурсов - отложены по оси абсцисс.

С достаточной для ориентировочных расчетов на стадии проектирования системы точностью, на рабочем режиме функционирования учебного заведения график 3.4 может быть аппроксимирован степенной функцией

, - (3.9)

на рисунке линия 2.

Примечание. При моделировании производственной функции равенством (3.9) параметры и следует выбирать так, чтобы кривая проходила через точку C (см. рис. 3.4) и наилучшее приближение имело место на участке .

Прежде чем перейти к основной задаче, связанной с определением оптимальных режимов работы, остановимся на возможности использования простейшей модели, представленной функцией (3.9). В этой функции

коэффициенту поставим в соответствие величину амортизационных расходов, характеризующих повышение качества и производительность основных средств производства (оборудование лабораторий, мастерских и т.п.), а параметру - качество учебного процесса - его целесообразность и организованность. При одном и том же основном оборудовании эффективность применения данного процесса определяется организацией всего технологического цикла. В случае рационально построенной технологии обучения увеличение количества вводимых ресурсов приводит к увеличению качества подготовки обучающихся. В то же время, если в точно согласованный технологический процесс обучения ввести излишнее количество ресурсов, произойдет уменьшение рентабельности.

Эти особенности производства четко представлены на рис.3.4. На характеристиках 1 и 2, изображенных на рисунке, участки AВ и A₁B₁ соответствуют рабочему режиму. Точка A отображает режим, когда учебное заведение работает по полному технологическому циклу, но еще не загружено оптимально. Точка C(C₁) отображает режим нормальной (оптимальной) нагрузки, когда учебное заведение дает максимальную прибавочную стоимость.

В связи с этим возникает необходимость определить, что такое прибавочная стоимость учебного заведения.

Под прибавочной стоимостью учебного заведения мы будем подразумевать разность между стоимостью продукции, которую будет способен производить выпускник учебного заведения к стоимости продукции, затраченной на его обучение.

Точка В изображает режим предельной загрузки, когда в результате введения излишних ресурсов рентабельность учебного заведения при данной технологии обучения обращается в нуль. В этом случае за счет введения дополнительных ресурсов повысить качество подготовки невозможно. Для повышения качества необходимо изменить технологию обучения.

На рис.3.4 кроме производственной функции, представленной в виде логистической функции (3.8), изображен луч 3, представляющий соотношение

,

выражающее цену затрачиваемых оборотных средств и основного оборудования в режиме, когда прибавочная стоимость равна нулю. Как видно из рисунка, в оптимальном режиме величина прибавочной стоимости определяется максимальным значением разности

. (3.10)

Примечание. При таком представлении производственной функции издержки на амортизацию основных фондов включены в член , что означает их линейную зависимость от количества переработанных ресурсов. Очень часто при квазистационарном режиме функционирования их учитывают отдельно. В ином случае производственную функцию нужно заменить на

, (3.11)

где - средняя величина амортизации при квазистационарном режиме функционирования учебного заведения.

Здесь необходимо отметить одно фундаментальное обстоятельство -производственная функция, записанная в формуле (3.9), выражает важнейший экономический закон, закон прибавочной стоимости.

Разность (3.10) отображает повышение стоимости готовой продукции за счет рациональной организации труда, в результате чего стоимость готовой продукции выше величины издержек на ее производство. В то же время стоимость не является полной рыночной оценкой произведенного продукта, в нашем случае - стоимость будущего труда выпускника учебного заведения.

Как уже отмечалось, рыночная стоимость продукции определяется не только эндогенными параметрами производящей системы. Решающим фактором, определяющим рыночную стоимость продукции, является конъюнктура. В условиях стабильной конъюнктуры рыночная стоимость (доход), который в дальнейшем обозначается буквой , должна удовлетворять условию

(3.12)

В общем случае доход отличается от средней стоимости произведенной продукции, определяемой конъюнктурой. Таким образом, готовая продукция имеет две оценки: стоимость , определяемую эффективностью производственного процесса, и доход - оценку, учитывающую реальную ситуацию на рынке труда. (Степенная функция, изображенная на рис.3.11 (кривая 2), отображает только особенности производственного процесса). Колебания, вызванные изменениями конъюнктуры при определении стоимости, пока не учитываются, так как здесь рассматривается квазистационарный режим.

В самом деле, внутренняя рентабельность учебного заведения зависит от разности между стоимостью продукции и издержками. У предприятий, где издержки равны доходу, прибавочная стоимость равна нулю. Условие равенства прибавочной стоимости О соответствует состоянию, когда производственная функция пересекается с прямой, см. рис. 3.4.

Прежде всего отметим, что включать в рабочий участок характеристики участки, расположенные правее точки B или левее точки A, не следует. Этим участкам соответствуют режимы, где прибавочная стоимость отрицательна. Поэтому в дальнейшем под производственной функцией подразумевается только отрезок AB .

Теперь рассмотрим, в каких пределах могут меняться коэффициент и показатель степени - с тем, чтобы они могли объективно отражать реалии рационально функционирующего учебного заведения. Для этого в выражении (3.9) примем =1, . Тогда степенная функция обратится в уравнение прямой

=1.

Пусть производится модернизация основного оборудования. Это означает, что параметр принимает ряд значений , таких, что . Получим пучок лучей, проходящий через начало координат. Чем больше значение , тем быстрее растет функция . Это свойство модели хорошо интерпретирует тривиальную истину: чем выше качество технологического оборудования, тем эффективнее перерабатываются ресурсы и тем больше производится продукции (см. рис. 3.5).

Рис. 3.5. Зависимость производственной функции от параметра .

Для выяснения значения параметра - положим в функции (3.9) . (Качество, а значит и стоимость основного оборудования неизменны). Тогда формула имеет вид

.

Рассмотрим три случая . Для всех трех случаев функция изображена на рис. 3.6.

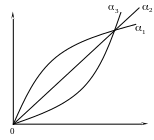
Рис. 3.6. Зависимость производственной функции от параметра .

Очевидно, что в случае, когда , на всем рабочем участке характеристики учебное заведение работает в убыток. Когда , учебное заведение не дает прибавочной стоимости, и только в случае учебное заведение ее создает.

Следовательно, останавливаясь на модели, представленной уравнением (3.9), нужно выбирать такую организацию производственного процесса, когда параметр наибольший, а параметр лежит в диапазоне и имеет минимальное значение.

В дальнейшем для описания производственного процесса -го, , учебного заведения будет использоваться модель учебного заведения, представленная производственной функцией.

.

Совокупность параметров , представляется в пространстве этих параметров, где величины и откладываются вдоль декартовых осей координат. Величина , характеризующая -е учебное заведение, называется модулем вектора производственных параметров.

И коэффициент , и показатель степени являются сложными функциями параметров векторов и многих внешних факторов. Подробно о векторах качества и технического уровня см. выше, а также в [3.1].