Оценка генеральной доли по собственно-случайной выборке. Несмещенность и состоятельность выборочной доли.
Пусть генеральная
совок-ть содержит N элементов, из к-ых М
обладает нек-ым признаком А. Следует
найти «наилучшую» оценку генеральной
доли
.
Рассмотрим в качестве такой возможной
оценки параметра р его статистический
аналог - выборочную долю
.
а) Выборка повторная.
В
ыборочную
долю можно представить как среднюю
арифметическую n альтернативных случайных
величин
,
т.е.
,
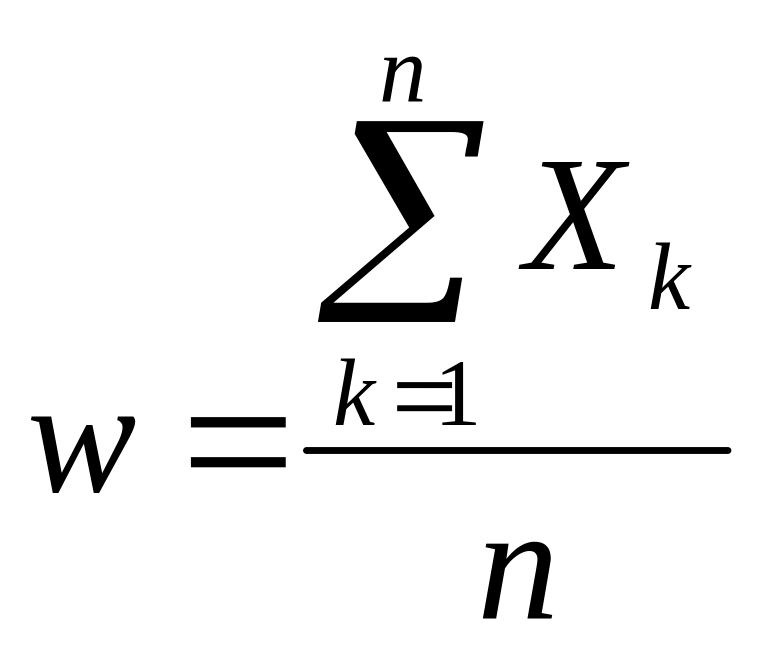где каждая СВ
(k=1,2,…,n)
выражает число появлений признака в
k-м
элементе выборки (т.е. при наличии
признака
,
при его отсутствии
)
и имеет один и тот же закон распределения:
Случайные величины независимы.
Теорема.
Выборочная доля
повторной выборки есть несмещенная и
состоятельная оценка генеральной доли
причем ее дисперсия:
,
Где q
= 1 – p.
☺ Докажем вначале несмещенность оценки w.
Матем-кое ожидание и дисперсия частости события в n независимых испытаниях, в каждом из к-рых оно может наступить с одной и той же вероятностью р, равны соответственно
,
.
Т.к. вер-ть того, что любой отобранный в выборку элемент обладает признаком А, есть генеральная доля р, то из 1 равенства вытекает, что частость или выборочная доля w есть несмещенная оценка генеральной доли р.
Осталось доказать
состоятельность
оценки
,
к-ая следует из теоремы Бернулли:
,
или
.
☻
б) Выборка бесповторная.
В случае бесповторной
выборки СВ
будут
зависимыми.
Теорема. Выборочная доля бесповторной выборки есть несмещенная и состоятельная оценка генеральной доли , причем ее дисперсия:
.
☺ Очевидно, что и для бесповторной выборки , т.е. w - несмещенная оценка для генеральной доли . Это связано с тем, что мат-кое ожидание суммы любых случайных величин равно сумме их мат-ких ожиданий (в том числе суммы зависимых случайных величин, каковой является выборочная доля w бесповторной выборки).
Найдем дисперсию выборочной доли для бесповторной выборки:
,
При выводе формулы
использовали то, что СВ Х = m
в случае бесповтoрной выборки имеет
гипергеометрическое распределение, и
ее дисперсия определяется по формуле
.
Оценка генеральной средней по собственно-случайной выборке. Несмещенность и состоятельность выборочной средней.
Пусть из генеральной совокупности объема N отобрана случайная выборка , где Xk - СВ, выражающая значение признака у k-гo элемента выборки (k=1,2, ...,n). Следует найти «наилучшую» оценку для генеральной средней.
Рассмотрим в
качестве такой возможной оценки
выборочнyю среднюю х, т.е.
.
а) Выборка повторная.
Закон распределения для каждой случайной величины (k=1,2,...,n) имеет вид:
С
лучайные
величины
независимы, т.к. независимы любые события
(k=1,2,...n;
i=1,2,...,m) и их комбинации.
Найдем числовые характеристики СВ :
,
(1)
.
(2)
т.е. мат-кое ожидание и дисперсия каждой СВ - это соот-но генеральная средняя и генеральная дисперсия.
Теорема.
Выборочная средняя
повторной выборки есть несмещенная и
состоятельная оценка генеральной
средней
причем
.
□ Докажем вначале несмещенность оценки. Найдем мат-кое ожидание выборочной средней , учитывая (2) и то, что - независимые случайные величины:
.
Осталось доказать
состоятельность оценки
,
которая следует непосредственно из
теоремы Чебышева:
или
б) Выборка бесповторная
В этом случае случайные величины будут зависимыми.
Теорема. Выборочная средняя бесповторной выборки есть несмещенная и состоятельная оценка генеральной средней , причем
.