28.Функция Лапласа и ее связь с функцией распределения нормальной случайной величины.

1) Распределение N(0;1) наз-ся станд-ным нормальным..Для стандартного распред-я плотность вер-ти равна: , а ф-я распред-я .

Ф-я Лапласа 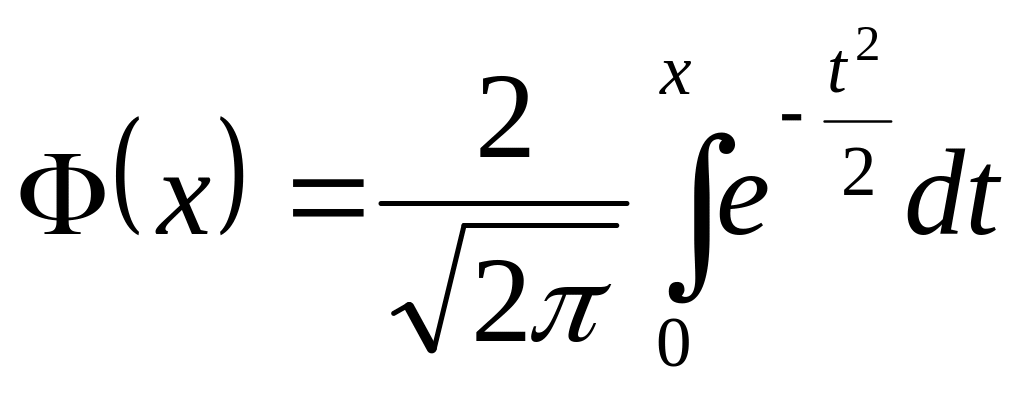и ф-я распред-я НСВ Х с параметрами связаны соотнош-м: .

2)Получим формулу д/вычисления вер-ти попадания НСВ с параметрами в задан. интервал(α;β) через стандарт-е распред-е :

3)3σ Вер-ть того, что НСВ отклоняется от своего мат.ожид-я по модулю меньше, чем ε>0, определяется формулой . Если положить , то получим .

Отсюда вытекает, что среди 10000 значений НСВ в среднем только 27 выйдут за пределы интервала . Это означает, что практически среди небольшого числа значений Х нет таких, кот. выходят за пределы указанного интервала. Правило 3-х сигм часто применяется д/грубой оценки сигма: .

29.Моменты случайных величин. Асимметрия и эксцесс.

Моментом n-го порядка Х по отн-ию к знач-ию а M_n(a)=M(X-a)ⁿ, а=0-начальный момент ύ_n

ф=Ь(Ч)-центральный μ_n

Для ДСВ: ύ_n=

Для НСВ: ύ_n=

Можно показать что справедлива формула:

μ_n=

μ₂₌ύ₂-ύ₁²

μ₃=ύ₃-3ύ₂ ύ₁+2ύ₁²

μ₄=ύ₄-4ύ₁ ύ₃+6ύ₁² ύ₂-3ύ₁⁴

На практике при изуч. распределения отличного от норм. необх. колич. оценить эти различия для этого вводятся вспомог.числ. хар-ки

ассиметрия и эксцесс.Центр.

момент 3-го порядка μ₃ характ-ет отклонение распределения СВХ от симметрии относит. мат.ожид.За меру этого отклонения берут число:

α = μ₃/σ³(х)-коэф.ассиметрии.

Ассиметрия всех распред-ий графики которых симметр. относит.прямой х=а=М(х) равна 0. Центр.момент 4-го порядка μ₄ служит для хар-ки крутости распред-ия СВ Х по сравнению с крутостью распред-ия НСВ с мат.ожид.и дисп. такими же как и у Х.За меру этой крутости берут число: χ = [ μ₄/σ⁴(х) ] -3

30.Функция распределения, плотность распределения двумерной случайной величины и их свойства. Закон распределения составляющих .Функцией распределения F(x, y) двумерной случайной величины (X, Y) называется вероятность того, что X < x, a Y < y:

                              F( х, у ) = p ( X < x, Y < y ).                                         (8.1)

                                                                                                                                    

                Рис.1Это означает, что точка (X, Y) попадет в область, заштрихованную на рис. 1, если вершина прямого угла располагается в точке (х, у).Плотностью совместного распределения вероятностей (двумер-ной плотностью вероятности) непрерывной двумерной случайной величины называ-ется смешанная частная производная 2-го порядка от функции распределения:   .                                                        (8.2)Замечание. Двумерная плотность вероятности представляет собой предел отношения вероятности попадания случайной точки в прямоугольник со сторонами Δх и Δу к площади этого прямоугольника при             Свойства двумерной плотности вероятности.1)      f(x, y) ≥ 0 (см. предыдущее замечание: вероятность попадания точки в прямоуголь-ник неотрицательна, площадь этого прямоугольника положительна, следовательно, предел их отношения неотрицателен).

2)      (cледует из определения двумерной плотности вероятно-сти). 3)      (поскольку это вероятность того, что точка попадет на плос-кость Оху, то есть достоверного события). Условной плотностью φ(х/у) распределения составляющих Х при данном значении Y = у называется                                     .                            

  Аналогично определяется условная плотность вероятности Y  при Х = х                                      .