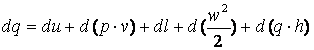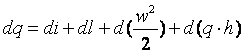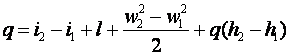10.Энтропия

Энтропи́я (от др.-греч. ἐντροπία — поворот, превращение) — в естественных науках мера неупорядоченности системы, состоящей из многих элементов. В частности, в статистической физике — мера вероятности осуществления какого-либо макроскопического состояния; в теории информации — мера неопределённости какого-либо опыта (испытания), который может иметь разные исходы, а значит, и количество информации; в исторической науке, для экспликации феномена альтернативности истории (инвариантности ивариативности исторического процесса).

Энтропия в информатике — степень неполноты, неопределённости знаний.

Энтропия — мера неупорядоченности системы.

Явление, обратное энтропии, именуется негэнтропией.

Понятие энтропии впервые было введено Клаузиусом в термодинамике в 1865 году для определения меры необратимого рассеивания энергии, меры отклонения реального процесса от идеального. Определённая как сумма приведённых теплот, она является функцией состояния и остаётся постоянной при замкнутых обратимых процессах, тогда как в необратимых — её изменение всегда положительно.

,

где   — приращение энтропии;   — минимальная теплота, подведённая к системе;   — абсолютная температура процесса.

• Термодинамическая энтропия — термодинамическая функция, характеризующая меру неупорядоченности термодинамической системы, то есть неоднородность расположения и движения её частиц.

11. 1 Закон

Первое начало термодинамики — один из трёх основных законов термодинамики, представляет собой закон сохранения энергии для термодинамических систем.

Изменение полной энергии системы в квазистатическом процессе равно количеству теплоты  , сообщённому системе, в сумме с изменением энергии, связанной с количеством вещества   при химическом потенциале  , и работы  ^[3], совершённой над системой внешними силами иполями, за вычетом работы  , совершённой самой системой против внешних сил

.

Для элементарного количества теплоты  , элементарной работы   и малого приращения   внутренней энергии первый закон термодинамики имеет вид:

.

Разделение работы на две части, одна из которых описывает работу, совершённую над системой, а вторая — работу, совершённую самой системой, подчёркивает, что эти работы могут быть совершены силами разной природы вследствие разных источников сил.

Важно заметить, что   и   являются полными дифференциалами, а   и   — нет.

Важным следствием первого закона термодинамики является утверждение о невозможности создания машины, способной совершать полезную работу без потребления энергии извне и без каких-либо изменений внутри самой машины. Такая гипотетическая машина получила название вечного двигателя (perpetuum mobile) первого рода. Многочисленные попытки создать такую машину неизменно заканчивались провалом. Любая машина может совершать положительную работу A над внешними телами только за счет получения некоторого количества теплоты Q от окружающих тел или уменьшения ΔU своей внутренней энергии.

12.

Используя понятие энтальпии, первый закон термодинамики можно записать в виде

При количественном анализе процессов часто используется математическая запись первого закона термодинамики через энтальпию:

, Дж,	(2.13)
, Дж / кг,	(2.14)
,	(2.15)
,	(2.16)
.

13. Уравнение первого закона термодинамики для движущегося рабочего тела

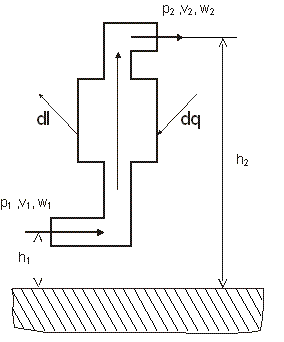
Уравнение первого закона для единицы массы стационарного потока (т. е. потока, параметры которого в любом сечении со временем не изменяются) можно вывести с помощью модели, показанной на рис. 3.2.

Рис. 3.2. К выводу уравнения первого закона термодинамики для движущегося рабочего тела

Здесь поток получает теплоту dq, совершает техническую работу dl, а также работу за счет изменения его кинетической энергии d(w²/2) и работу против силы тяжести d(g*h) вследствие изменения его высоты над уровнем моря (h=h₂-h₁). Кроме того, имеет место работа вталкивания газа p₁*v₁ и выталкиванияp₂*v₂. Их разность l_пр=p₂*v₂-p₁*v₁ называют работой проталкивания. Учитывая сказанное можно записать закон сохранения энергии для движущегося рабочего тела

(3.9)

Здесьu – внутренняя энергия рабочего тела.

Так как по определению u+p*v=i, полученное выражение можно переписать следующим образом

После интегрирования получим

(3.10)

14.

Дросселирование (от нем. drosseln — душить) — понижение давления газа или пара при протекании через сужение проходного канала трубопровода — дроссель, либо через пористую перегородку.

Дросселирование является близким к идеальному осуществлением процесса Джоуля-Томсона. Дросселирование можно рассматривать^[1] как изоэнтальпийныйквазиравновесный процесс и проводить, основываясь на выражении

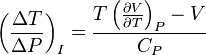
дифференциального эффекта Джоуля-Томсона, интегрирование следующим образом:

 — интегральный эффект Джоуля-Томсона.

15.