31. Плотность распределения двумерной случайной величины

 Двумерной случайной величиной называют систему из двух случайных величин  , для которой определена вероятность   совместного выполнения неравенств   и  , где x и y - любые действительные числа.     Функция двух переменных

 Двумерная случайная величина   называется дискретной, если   и   - дискретные величины.     Пусть возможные значения   и   образуют, например, конечные последовательности x₁, x₂, ..., x_n и y₁, y₂, ..., y_s. Возможные значения двумерной случайной величины   имеют вид (x_i, y_j), где i=1, 2, ..., n; j=1, 2, ..., s. Обозначим через p_ij вероятность того, что     

   Функция распределения F(х, у) имеет вид   

   где двойная сумма распространена на те i и j, для которых x_i<x и y_j<y. 

 Сумма всех вероятностей   

   Две дискретные случайные величины   и   называются независимыми, если для всех пар i, j выполняется соотношение   

Непрерывные случайные величины   и   называются независимыми, если  , где   и   - соответственно плотности распределения вероятностей случайных величин   и  . В этом случае   

   где F₁(x) и F₂(y) — соответственно функции распределения величин   и 

 Зная функцию распределения F(х,у) двумерной случайной величины  , легко найти как функцию распределения, так и плотность распределения каждой из случайных величин  и  , в отдельности.     Действительно, пусть F₁(x) - функция распределения случайной величины  . Тогда  . Так как в этом случае   может принимать любое значение, то ясно, что   

 Двумерная случайная величина   имеет плотность распределения   

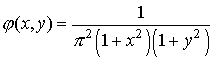
По определению двумерная случайная величина   распределена нормально, если плотность распределения системы величин   и   имеет вид   

32.Условные законы распределения

Пусть известна плотность распределения системы двух случайных величин. Используя свойства функций распределения, можно вывести формулы для нахождения плотности распределения одной величины.

Перейдем теперь к решению обратной задачи: по известным законам распределения отдельных величин, входящих в систему, найти закон распределения системы. Легко увидеть, что в общем случае эта задача неразрешима. Действительно, с одной стороны, законы распределения отдельных случайных величин, входящих в систему, характеризуют каждую из случайных величин в отдельности, но ничего не говорят о том, как они взаимосвязаны. С другой стороны, искомый закон распределения системы должен содержать все сведения о случайных величинах системы, в том числе и о характере связей между ними.

Таким образом, если случайные величины   взаимозависимы, то закон распределения системы не может быть выражен через законы распределения отдельных случайных величин, входящих в систему. Это приводит к необходимости введения условных законов распределения.

Распределение одной случайной величины, входящей в систему, найденное при условии, что другая случайная величина, входящая в систему, приняла определенное значение, называется условным законом распределения.

Условный закон распределения можно задавать как функцией распределения, так и плотностью распределения. Условная функция распределения обозначается  , условная плотность распределения —   (мы записали условные законы распределения случайной величины   при условии, что другая случайная величина   приняла определенное значение).

Плотностью распределения для случайной величины   при условии, что случайная величина   приняла определенное значение (условной плотностью распределения), назовем величину

Аналогично плотностью распределения для случайной величины   при условии, что случайная величина   приняла определенное значение, назовем величину

. Отсюда получаем  .

или с учетом формул (5.3)

Условная плотность распределения обладает всеми свойствами безусловной плотности распределения. В частности,