
- •-Параметры напряженно-деформируемого состояния (ндс) конструкции:
- •-Изображение основных схем правильного и неправильного соединения элементов кинематической цепи:
- •-Алгоритм кинематического анализа:
- •-Формы определения внутренних усилий в статически определимых системах
- •-Термины и обозначения:
- •-Разновидности статического метода определения внутренних усилий в стержнях простых ферм при узловом нагружении:
- •-Формулы для определения опорных реакций трехшарнирной арки при действии вертикальной нагрузки
-Формы определения внутренних усилий в статически определимых системах
1.аналитическая 2.графическая 3.матричная
-Статический метод определения внутренних усилий основан на использовании метода сечений и рассмотрении условий равновесия конструкции в целом или отдельных её частей.
-Кинематический метод определения внутренних усилий основан на использовании принципа возможных перемещений для несвободной механической системы.
-Дискретизация расчетной схемы конструкции предполагает ее разбиение на отдельные элементы, введение мест их соединения и выделение расчетных сечений конструкции.
-Дискретизация внешней нагрузки конструкции заключается в замене заданной нагрузки статически эквивалентной системой сосредоточенных сил, приложенных в узлах дискретной расчетной схемы.
-Матрица влияния внутреннего усилия
Матричная
форма линейных соотношений имеет вид
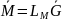 .
.
Входящая в
эту формулу матрица
 осуществляет линейное преобразование
нагрузки
осуществляет линейное преобразование
нагрузки
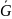 в искомый вектор балочных изгибающих
моментов
в искомый вектор балочных изгибающих
моментов
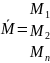 и называется матрицей влияния изгибающих
моментов
и называется матрицей влияния изгибающих
моментов
3.
-Виды подвижных нагрузок:
1.двухосная подвижная нагрузка (кары, автомобили)
2.многоосная подвижная нагрузка (одновременное движение двухосных механических экипажей, ж/д составы)
3.гусеничная нагрузка (различные виды движущихся механических экипажей на гусеничном ходу, трактор)
-Опасное положение подвижной нагрузки – положение подвижной нагрузки, при которой требуемые величины принимают экстремальные значения
-Подходы к отысканию опасных положений подвижных нагрузок:
1.первый подход основан на получении аналитических выражений, определяющих непрерывные изменения искомых величин в зависимости от положения подвижной нагрузки на конструкции. Исследуя полученные функции методами мат.анализа, можно найти их наибольшие и наименьшие значения.
2.второй подход основан на понятии линии влияния. Он справедлив только для линейно деформируемых систем, но дает для них общий метод отыскания опасных положений любых подвижных нагрузок
-Функция влияния внутреннего усилия. При движении единичной нагрузки любая величина Z (внутреннее усилие или перемещение), возникающая в конструкции, зависит только от абсциссы х и описывается некоторой функцией Z=f(х).
-Линия влияния внутреннего усилия некоторой величины Z, возникающей в определенном месте конструкции, называется график, описывающий изменение этой величины в зависимости от положения движущегося по конструкции вертикального сосредоточенного единичного груза.
-Отличия линии влияния внутреннего усилия от эпюры аналогичного внутреннего усилия:
1.эпюра некоторого внутреннего усилия описывает его изменение по длине всей конструкции, а линия влияния описывает изменение этого внутреннего усилия в одном определенном месте конструкции (опора, сечение)
2.Эпюра внутренних усилий связана с действием реальной неподвижной нагрузки, заданной в одном определенном положении, а линия влияния порождается действием искусственной подвижной нагрузки, которая может занимать различные положения на конструкции.
-Статический способ построения линий влияния внутренних усилий основан на составлении уравнений равновесия для конструкции, нагруженной в произвольном месте с абсциссой х неподвижным единичным грузом, и определении из этих уравнений внутреннего усилия как некоторой функции от х.
-Запишите функции влияния опорных реакций простой двухконсольной балки и получите с их помощью линии влияния. (УМК, стр. 60.)
-Запишите функцию влияния изгибающего момента простой двухконсольной балки в произвольном сечении пролета и получите с ее помощью линию влияния.(УМК, стр.61)
- Запишите функцию влияния изгибающего момента простой двухконсольной балки в произвольном сечении консоли и получите с ее помощью линию влияния.
-Запишите функцию влияния поперечной силы простой двухконсольной балки в произвольном сечении пролета и получите с ее помощью линии влияния.(УМК, стр. 62)
-Запишите функцию влияния поперечной силы простой двухконсольной балки в произвольном сечении консоли и получите с ее помощью линии влияния.
-Общий порядок построения линий влияния внутренних усилий кинематическим способом
1.удалить связь, линию влияния реакции которой требуется построить, и заменить удаленную связь соответствующей реакцией положительного направления. Приемами удаления связей являются отбрасывание стержня, введение в сечение шарнира или «качелей».
2.придать полученному механизму возможное отклонение, направление которого задается в соответствии с положительным направлением реакции удаленной связи.
3.выбрать специальный масштаб для отклоненного положения механизма, при котором перемещение по направлению реакции удаленной связи полагается равным 1.
-Формула для определения внутреннего усилия по линиям влияния от неподвижной сосредоточенной силы:
Пусть к
конструкции приложена сосредоточенная
сила Р1 на расстоянии а1 от
левой опоры. Ордината линии влияния под
местом приложения силы имеет некоторое
значение s1. Исходя
из смысла ординаты линии влияния и
существования прямой пропорциональной
зависимости внутреннего усилия S
от силы Р1, получим следующую
формулу для определения S
:
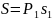
-Формула для определения внутреннего усилия по линиям влияния от неподвижной системы сосредоточенных сил:
Пусть к
конструкции приложена система
сосредоточенных сил Рi
на расстояниях аi
от левой опоры. Ординаты линии влияния
под местом приложения сил имеет некоторое
значение si
. Исходя из принципа независимости
действия сил и с учетом формулы
получим следующую формулу для определения
S :
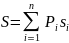
.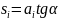 и получим
и получим
 , где
, где
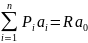 .
Отсюда следует, что усилие S
равняется:
.
Отсюда следует, что усилие S
равняется:

- Формула для определения внутреннего усилия по линиям влияния от неподвижной распределенной нагрузки постоянной интенсивности:
Пусть к
конструкции на некотором участке [а,b]
приложена распределенная нагрузка с
переменной интенсивностью g(x).
Выделим элементарный участок dx
и определим для него равнодействующую
нагрузки R=g(x)dx.
Тогда, применяя
и выполняя интегрирование на участке
[а,b], получим следующую
формулу для определения S
:
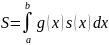 .
При постоянной интенсивности g
можно вынести за знак интеграла и тогда
формула примет вид :
.
При постоянной интенсивности g
можно вынести за знак интеграла и тогда
формула примет вид :
 .
.
- Формула для определения внутреннего усилия по линиям влияния от неподвижного внешнего момента:
Пусть к
конструкции приложен момент М1
на расстоянии а1 от левой опоры.
Представим заданный момент в виде пары
вертикальных сил с плечом dx.
Ординаты линии влияния под местами
приложения заменяющих сил M1/dx
, соответственно, имеют значения s
и s+ds. Тогда,
применяя
, получим следующую формулу для определения
S:

-Формула для определения внутреннего усилия по линиям влияния от системы неподвижных внешних моментов:
Пусть к конструкции приложена система моментов Мi на расстояниях аi от левой опоры. Тангенсы углов наклона касательных к линии влияния под местами их приложения имеют значения tgα1. Исходя из принципа независимости действия сил и с учетом получим следующую формулу для определения S:
.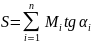
- Формула для определения max и min значений внутренних усилий по линиям влияния от временной нагрузки
-Связь линии влияния внутреннего усилия с матрицей влияния этого усилия:
С помощью линий влияния внутренних усилий можно формировать матрицы влияния этих усилий по строкам. Использование единичных эпюр внутренних усилий позволяет формировать матрицы влияния по столбцам.
4.
-Деформация конструкции – изменение формы и размера конструкции при приложении к ним внешних воздействий.
-Дифференциальные количественные характеристики деформации конструкции описывают происшедшие изменения формы и размеров конструкции в окрестности ее произвольной точки (относительной линейной деформацией ε и углом сдвига ϒ)
-Интегральные количественные характеристики деформации конструкции описывают происшедшие изменения формы и размеров конструкции в целом (линейное и угловое перемещения).
-Жесткость конструкции зависит от применяемого конструкционного материала, жесткости конструктивных элементов и способов соединения этих элементов между собой.
-Жесткость конструкционного материала характеризуется отношением жесткости поперечного сечения к длине элемента и называется его погонной жесткостью при изгибе, растяжении-сжатии или сдвиге.
-Подходы к определению перемещений:
1.один подход связан с определением малых перемещений, и он справедлив для жестких конструкций. Такие конструкции обычно относятся к линейно-деформируемым системам. Согласно этому подходу определяются перемещения, которые малы по сравнению с размерами самой конструкции.
2.второй подход позволяет определять большие перемещения, и он справедлив для гибких конструкций. Такие конструкции обычно относятся к геометрически нелинейным системам. Согласно этому подходу определяются перемещения, которые не малы по сравнению с размерами самой конструкции.
-Цели определения перемещений конструкции:
1.для оценки пригодности конструкций к нормальной эксплуатации
2.
-Если к
конструкции по направлению номер j
приложить безразмерную силу
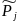 = 1, то возникающие в конструкции
перемещения по указанным выше направлениям
называют единичными перемещениями.
Такие перемещения обозначаются
= 1, то возникающие в конструкции
перемещения по указанным выше направлениям
называют единичными перемещениями.
Такие перемещения обозначаются
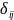 и их индексы указывают те же направления,
что и для частичных перемещений
и их индексы указывают те же направления,
что и для частичных перемещений
 . Единичные перемещения подразделяются
на собственные и побочные.
. Единичные перемещения подразделяются
на собственные и побочные.
-Законом
Гука для конструкции называется
соотношение
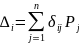 , согласно которому полное перемещение
, согласно которому полное перемещение
 является линейной функцией действующих
сил
является линейной функцией действующих
сил
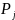 .
.
-Входящие в
 и
единичные перемещения играют роль
коэффициентов пропорциональности между
силами и перемещениями. Они позволяют
количественно оценивать способность
конструкции получать перемещения по
определенному направлению и поэтому
называются коэффициентами податливости.
и
единичные перемещения играют роль
коэффициентов пропорциональности между
силами и перемещениями. Они позволяют
количественно оценивать способность
конструкции получать перемещения по
определенному направлению и поэтому
называются коэффициентами податливости.
-Применим к каждому полному перемещению конструкции.
.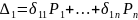
……………………………………..
.
Входящие в
полученные линейные соотношения
коэффициенты податливости
образуют квадратную матрицу, которая
называется матрицей податливости
конструкции. Тогда матричная запись
имеет вид
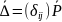 .
.
.
-Соотношения …………………………………….. , согласно которым действующие на конструкцию силы являются
.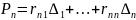
линейными
функциями её полных перемещений, являются
другой формой обобщенного закона Гука.
Входящие в эти соотношения коэффициенты
пропорциональности
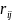 количественно характеризуют способность
конструкции сопротивляться возникновению
перемещений по определенному направлению,
называются коэффициентами жесткости
и образуют матрицу жесткости
конструкции (
).
Матричная запись имеет вид
количественно характеризуют способность
конструкции сопротивляться возникновению
перемещений по определенному направлению,
называются коэффициентами жесткости
и образуют матрицу жесткости
конструкции (
).
Матричная запись имеет вид
 .
.
-В общем случае при статическом нагружении стержневой конструкции на нее действует некоторая совокупность сосредоточенных сил, моментов и распределенных нагрузок. Если составляющие этой совокупности нагрузок изменяются пропорционально одному параметру Р, то она называется обобщенной силой.
-Под
обобщенным перемещением понимают
некоторую геометрическую величину,
связанную с деформированным состоянием
конструкции, произведение которой на
параметр обобщенной силы позволяет
вычислить действительную или возможную
работу заданной совокупности нагрузок
по одночленным формулам вида А =
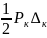 или А'= РΔ'к .
или А'= РΔ'к .
-Принцип возможных перемещений для деформируемой системы. Согласно этому принципу, если деформируемая система находится в равновесии, то сумма работ всех действующих сил, включая и внутренние силы, на возможных перемещениях системы от положения равновесия равняется нулю.
-Формула Максвелла-Мора для произвольной плоской стержневой конструкции
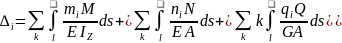
- Формула Максвелла-Мора для балок и плоских рам
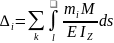
-Формула Максвелла-Мора для арок и комбинированных систем

-Формула Максвелла-Мора для ферм

-Формула для определения перемещений от действия температуры в статически определимой плоской стержневой конструкции
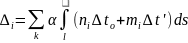
-Формула для определения перемещений от действия осадки опор в статически определимой плоской стержневой конструкции
-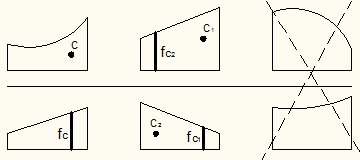 Правило
Верещагина. Определенный интеграл
от произведения двух функций, одна из
которых линейная, а вторая нелинейная,
равняется произведению площади графика
нелинейной функции на ординату графика
линейной функции, расположенную под
центром тяжести площади графика
нелинейной функции. В случае, если вторая
функция тоже является линейной, то при
пользовании формулой
Правило
Верещагина. Определенный интеграл
от произведения двух функций, одна из
которых линейная, а вторая нелинейная,
равняется произведению площади графика
нелинейной функции на ординату графика
линейной функции, расположенную под
центром тяжести площади графика
нелинейной функции. В случае, если вторая
функция тоже является линейной, то при
пользовании формулой
 безразлично, площадь графика какой
функции следует вычислять. Правило
знаков. Если график нелинейной
функции и ордината графика линейной
функции, расположены по одну сторону
оси, то результат положительный, в
противном случае он отрицательный.
безразлично, площадь графика какой
функции следует вычислять. Правило
знаков. Если график нелинейной
функции и ордината графика линейной
функции, расположены по одну сторону
оси, то результат положительный, в
противном случае он отрицательный.
- Границы применения правила Верещагина:
1. нелинейная + линейная
2. линейная + линейная
3. нелинейная
+ нелинейная (нельзя!)
-Теорема
о взаимности работ. Возможная работа
внешних сил i-того состояния
конструкции на перемещениях, вызванных
внешними силами k-того
состояния, равняется возможной работе
внешних сил k-того состояния
конструкции на перемещениях, вызванных
внешними силами i-того
состояния. ( )
)
-Теорема
о взаимности перемещений. Побочные
единичные перемещения конструкции с
различным порядком расположения
одинаковых индексов равны между собой.
( )
)
5.
-Реальная ферма представляет собой геометрически неизменяемую стержневую конструкцию с жестким соединением прямолинейных стержней в узлах.
-Расчетная схема фермы – это система, полученная при замене жестких узлов шарнирами
-При узловой нагрузки в прямолинейных стержнях фермы не возникают изгибающие моменты и поперечные силы, а продольные силы постоянны по длине каждого стержня.
-При узловой нагрузки в криволинейных стержнях фермы изгибающие моменты и поперечные силы не равны нулю, а продольные силы переменны по длине стержня.
-При внеузловой нагрузки в прямолинейных стержнях фермы изгибающие моменты и поперечные силы не равны нулю, а продольные силы переменны по длине стержня.
