- •1. Основные положения мкт. Идеальный газ.
- •Основные определения (давление, плотность количество вещества, константы и размерность)
- •2) Число молекул в вещества;
- •3) Число молекул в вещества;
- •Количество вещества можно найти по формуле
- •2. Основное уравнение мкт, температура, среднеквадратичная скорость
- •Основное уравнение молекулярно–кинетической теории записывается так:
- •Основное уравнение молекулярно–кинетической теории записывается так:
- •Основное уравнение молекулярно–кинетической теории записывается так:
- •Температура снизилась с до . Как изменилась при этом среднеквадратичная скорость молекул?
- •1) Уменьшилась в 2 раза;
- •3. Уравнение Менделеева-Клапейрона, газовые законы
- •Уравнение Менделеева–Клапейрона имеет вид
- •Уравнение Менделеева–Клапейрона имеет вид
- •Уравнение изобары имеет вид
- •4. Сложные задачи на газовые законы
- •5.Основные определения статистики Максвелла
- •6. Знание формул для статистики Максвелла, среднеквадратичная скорость
- •7.Распределение Больцмана (не везде знание формулы)
- •1) ; 2) ; 3)Обе формулы верны.
- •8. Длина свободного пробега
- •9. Термодинамика. Определения. 1-е начало. Простые вопросы.
- •10.Первое начало термодинамики для изопроцессов. Сложные формулы. Задачи.
- •11.Теплоёмкость, адиабатный процесс
- •12. Тепловые машины
- •13. Второе начало термодинамики. Энтропия
- •3. Обе формулы верны.
- •3. Обе формулы верны.
12. Тепловые машины
КПД тепловой машины находится по формуле
1)
![]() ; 2)
; 2)
![]() ; 3)
; 3)
![]() .
.
КПД тепловой машины находится по формуле
1)
![]() ; 2)
; 2)
![]() ; 3)
; 3)
![]() .
.
КПД тепловой машины находится по формуле
1)
![]() ; 2)
; 2)
![]() ; 3)
; 3)
![]() .
.
Выражение для КПД справедливо
1) только для тепловой машины, работающей по циклу Карно;
2) только для тепловой машины, работающей на идеальном газе;
3) для любой тепловой машины.
Выражение для КПД
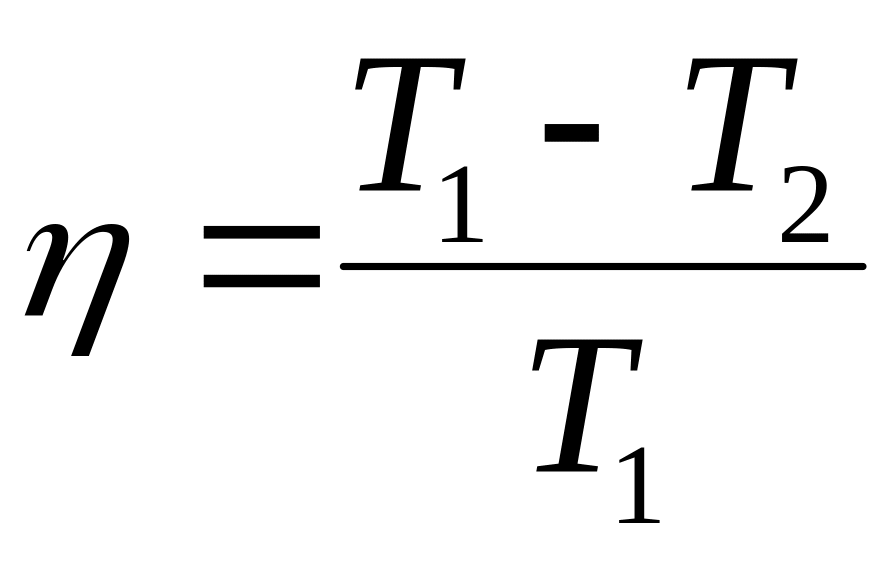 справедливо
справедливо
1) только для тепловой машины, работающей по циклу Карно;
2) только для тепловой машины, работающей на идеальном газе;
3) для любой тепловой машины.
КПД цикла Карно находится по формуле
1)
![]() ; 2)
; 2)
![]() ; 3)
.
; 3)
.
Для любой тепловой машины справедливо соотношение
1)
![]() ; 2)
; 2)
![]() ; 3)
; 3)
![]() .
.
Для идеальной тепловой машины, работающей по циклу Карно
1) выполненная работа меньше теплоты, переданной нагревателем;
2) выполненная работа больше теплоты, переданной нагревателем;
3) выполненная работа равна теплоте, переданной нагревателем.
Для любой тепловой машины
1) выполненная работа меньше теплоты, переданной нагревателем;
2) выполненная работа меньше теплоты, полученной холодильником;
3) выполненная работа меньше теплоты, переданной нагревателем и полученной холодильником.
Цикл Карно состоит из
1) двух изохор и двух адиабат;
2) двух изотерм и двух адиабат;
3) двух изобар и двух адиабат.
Тепловая машина 1/3 тепла, полученного от нагревателя, отдаёт холодильнику. Чему равен КПД такой машины?
1) 0,33; 2) 0,45; 3) 0,66.
Идеальная тепловая машина, работающая по циклу Карно1/3 тепла, полученного от нагревателя отдаёт холодильнику. Найти температуру холодильника, если температура нагревателя равна 270С.
1) 100 К; 2) 133 К; 3) 166 К.
КПД тепловой машины, получающей от нагревателя 450 Дж тепла, и отдающей холодильнику 140 Дж равен
1) 0,31; 2) 0,46; 3) 0,69.
КПД идеальной тепловой машины, имеющей температуру нагревателя 4500С, и холодильника 600С равен
1) 0,36; 2) 0,46; 3) 0,64.
Идеальная тепловая машина, работающая по циклу Карно, имеет КПД 30%. Найти температуру холодильника, если температура нагревателя равна 3000С.
1) 372 К; 2) 401 К; 3) 472 К.
Что выгоднее для повышения КПД идеальной тепловой машины
1) повысить температуру нагревателя на 200;
2) понизить температуру холодильника на 200;
3) одинаково.
КПД идеальной тепловой машины
1) равен 1;
2) определяется температурами нагревателя и холодильника;
3) определяется трением в машине.
Цикл Карно правильно показан на рисунке

Цикл Карно правильно показан на рисунке

Цикл Карно правильно показан на рисунке

13. Второе начало термодинамики. Энтропия
Обратимым называется процесс, удовлетворяющий условию
1) после прохождения процесса в окружающей среде не должно произойти никаких изменений;
2) процесс может идти в прямом и обратном направлениях;
3) необходимо выполнение обоих условий.
Второе начало термодинамики можно сформулировать так
1) невозможно построить тепловую машину, которая выполняла бы работу, большую теплоты, полученной от нагревателя;
2) невозможно построить тепловую машину, которая выполняла бы работу только за счёт охлаждения некоторого тела;
3) обе формулировки эквивалентны.
Второе начало термодинамики можно сформулировать так
1) невозможно построить тепловую машину, которая выполняла бы работу, большую теплоты, полученной от нагревателя;
2) невозможен процесс, единственным результатом которого была бы передача тепла от холодного тела к горячему;
3) обе формулировки эквивалентны.
Второе начало термодинамики можно сформулировать так
1) невозможно построить тепловую машину, которая выполняла бы работу только за счёт охлаждения некоторого тела;
2) невозможен процесс, единственным результатом которого была бы передача тепла от холодного тела к горячему;
3) обе формулировки эквивалентны.
Микросостояние системы описывается
1) набором термодинамических параметров системы;
2) набором координат и скоростей всех молекул;
3) обе формулировки эквивалентны.
Макросостояние системы описывается
1) набором термодинамических параметров системы;
2) набором координат и скоростей всех молекул;
3) обе формулировки эквивалентны.
Термодинамическая вероятность определяется
1) числом микросостояний, возможных для данного макросостояния;
2) числом микросостояний, возможных для данной температуры;
3) числом микросостояний, возможных для данной энергии системы.
Энтропия замкнутой термодинамической системы
1) не может возрастать;
2) остаётся постоянной;
3) не может убывать.
При необратимых процессах энтропия
1) возрастает;
2) убывает;
3) может возрастать и убывать.
При обратимых процессах энтропия
1) остаётся неизменной;
2) убывает;
3) может возрастать и убывать.
Для обратимых процессов справедливо
1)
![]() ; 2)
; 2)
![]() ; 3)
; 3)
![]() .
.
Для необратимых процессов справедливо
1)
![]() ; 2)
; 2)
![]() ; 3)
.
; 3)
.
При выполнении цикла Карно энтропия
1) возрастает;
2) убывает;
3) не меняется.
Т
 ермодинамическая
вероятность указанного состояния
системы, состоящей из 4 молекул, равна
ермодинамическая
вероятность указанного состояния
системы, состоящей из 4 молекул, равна
1) 2; 2) 4; 3) 6.
Т
 ермодинамическая
вероятность указанного состояния
системы, состоящей из 4 молекул, равна
ермодинамическая
вероятность указанного состояния
системы, состоящей из 4 молекул, равна
1) 2; 2) 4; 3) 6.
Энтропия с термодинамической вероятностью связана соотношением
1)
![]() ; 2)
; 2)
![]() ; 3)
; 3)
![]() .
.
Для обратимого процесса справедливо соотношение
1)
![]() ; 2)
; 2)
![]() ; 3)
; 3)
![]() .
.
Для необратимого процесса справедливо соотношение
1)
![]() ; 2)
; 3)
.
; 2)
; 3)
.
Изменение энтропии при превращении 1 кг воды в пар равно
1)
![]() ; 2)
; 2)
![]() ; 3)
; 3)
![]() .
.
Справка: удельная теплота парообразования воды 2.3·106 Дж/кг.
При
 ,
энтропия стремится к
,
энтропия стремится к
1) 0; 2) 1; 3)
![]() .
.
Колебания и волны.
Колебаниями называются
движения или процессы, обладающие той или иной степенью повторяемости во времени;
движения или процессы, при которых система через равные промежутки времени возвращается в исходное состояние;
движения или процессы, обладающие той или иной степенью повторяемости в пространстве.
Колебания называются периодическими, если
движения или процессы обладают той или иной степенью повторяемости во времени;
движения или процессы, при которых система через равные промежутки времени возвращается в исходное состояние;
движения или процессы обладают той или иной степенью повторяемости в пространстве.
Периодом колебаний называется
время, в течение которого смещение от положения равновесия дважды достигает одного и того же значения;
время, в течение которого система совершает одно полное колебание;
время, в течение которого смещение достигает амплитудного значения.
Периодические колебания в общем случае описываются уравнением

Гармоническими называются колебания, в которых зависимость смещения от времени описывается уравнением:

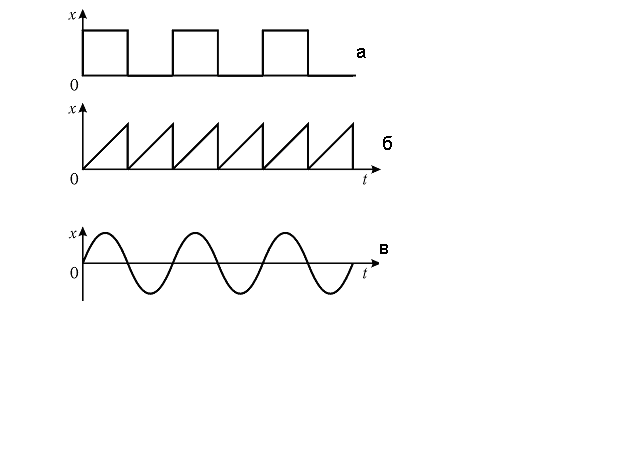
6. На рисунке показаны три типа периодических колебаний. Укажите, какое из них является гармоническим.
|
|
Амплитуда колебаний – это
путь, пройденный материальной точкой от положения равновесия до максимального отклонения;
максимальное по модулю отклонение от положения равновесия;
оба ответа правильные.
Циклическая частота колебаний численно равна
числу колебаний за единицу времени;
числу колебаний за время, равное периоду колебаний;
числу колебаний, совершаемых за
 секунд.
секунд.
8. Линейная частота колебаний численно равна
числу колебаний за единицу времени;
числу колебаний за время, равное периоду колебаний;
числу колебаний, совершаемых за секунд.
Герц – частота такого колебательного движения, в котором
за 1 с совершается одно полное колебание;
за с совершается одно полное колебание;
за время, равное периоду колебаний, совершается одно полное колебание.
Период колебаний – это
время, за которое совершается одно полное колебание;
время, за которое смещение достигает максимального значения;
время, за которое материальная точка переходит из состояния равновесия в состояние с максимальным смещением.
Между периодом колебаний и линейной частотой существует связь
![]()
Фаза
это – аргумент тригонометрической функции, который показывает, какая часть колебания выполнена к данному моменту времени, если полному колебанию сопоставит значение ;
показывает смещение от положения равновесия в начальный момент времени;
это – аргумент тригонометрической функции, который показывает, какая часть колебания выполнена к данному моменту времени, если полному колебанию сопоставит значение
 .
.
Начальная фаза
это – аргумент тригонометрической функции, который показывает, какая часть колебания выполнена к данному моменту времени, если полному колебанию сопоставит значение ;
показывает смещение от положения равновесия в начальный момент времени;
это – аргумент тригонометрической функции, который показывает, какая часть колебания выполнена к данному моменту времени, если полному колебанию сопоставит значение .
Дифференциальное уравнение гармонических колебаний имеет вид:

Дифференциальное уравнение затухающих колебаний имеет вид:
15. Дифференциальное уравнение вынужденных колебаний имеет вид:
Квазиупругой сила
всегда направлена к положению равновесия, а её значение пропорционально смещению от положения равновесия:
это один из видов потенциальных сил:
оба утверждения верны.
Гармоническое колебание совершается по закону косинуса с частотой ω0, начальной фазой φ0 и амплитудой А. При этом скорость изменяется по закону:

Гармоническое колебание совершается по закону косинуса с частотой ω0, начальной фазой φ0 и амплитудой А. При этом ускорение изменяется по закону:
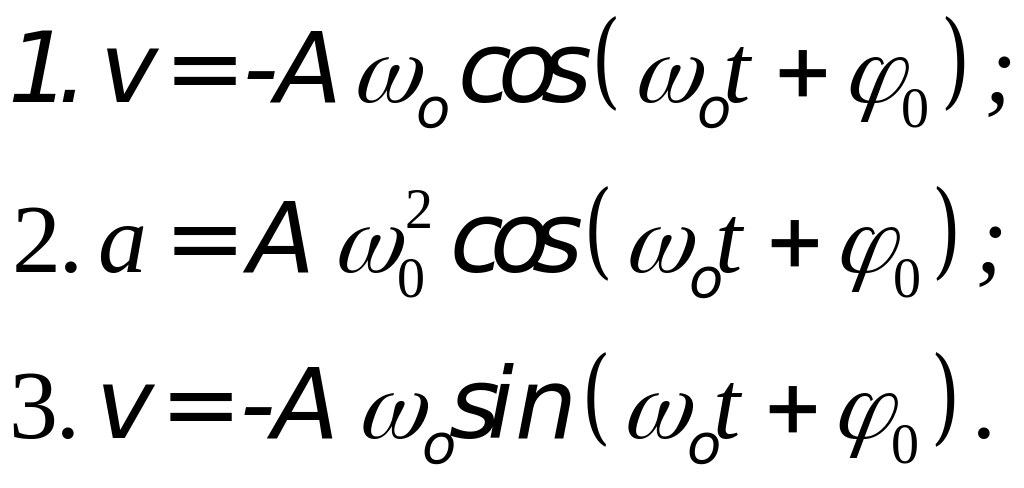
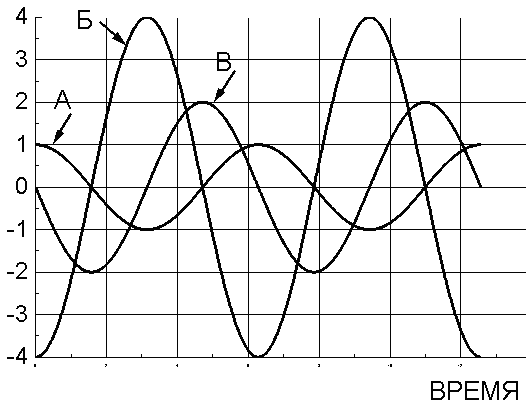
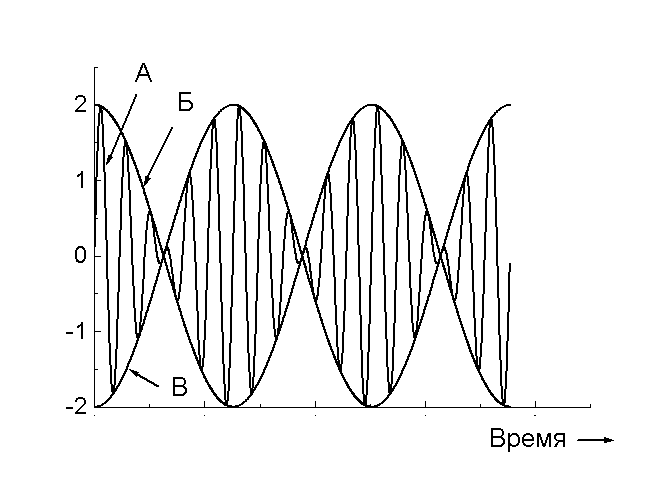
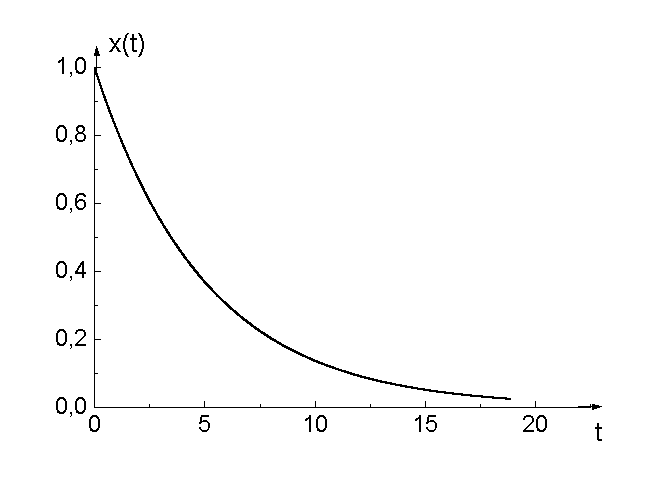
Гармоническое колебание совершается по закону косинуса с частотой ω0=1рад/с, начальной фазой φ0=0 и амплитудой А=1. Укажите график зависимости скорости от времени.
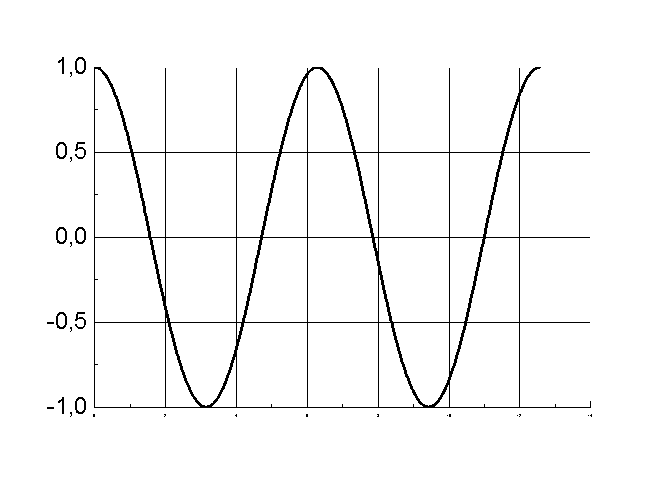
А
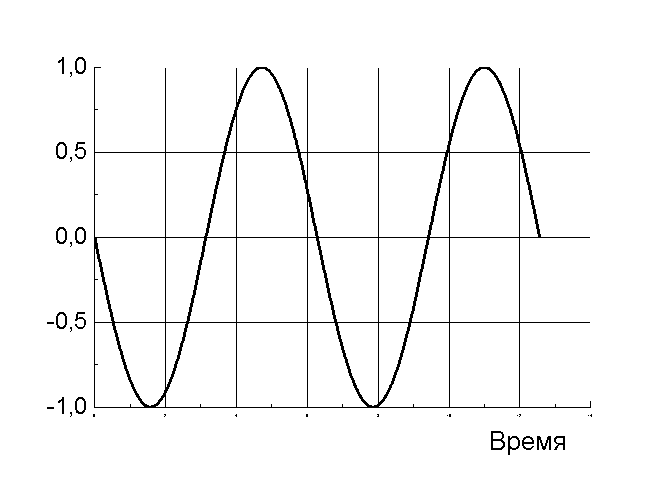
Б
В

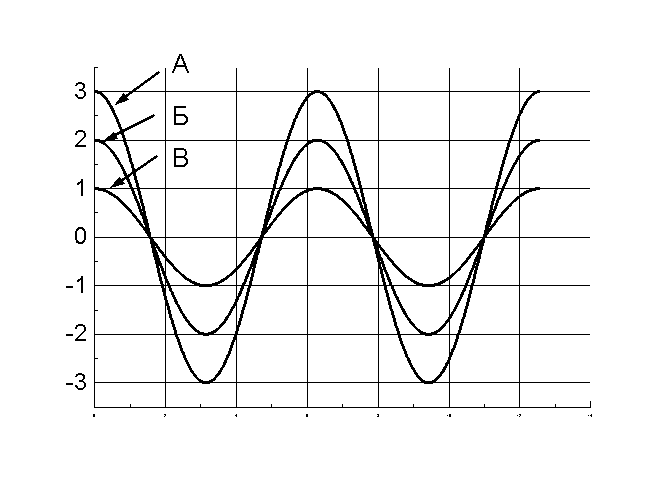
Гармоническое колебание совершается по закону косинуса с частотой ω0=1рад/с, начальной фазой φ0=0 и амплитудой А=1. Укажите график зависимости ускорения от времени.
А |
Б |
В |
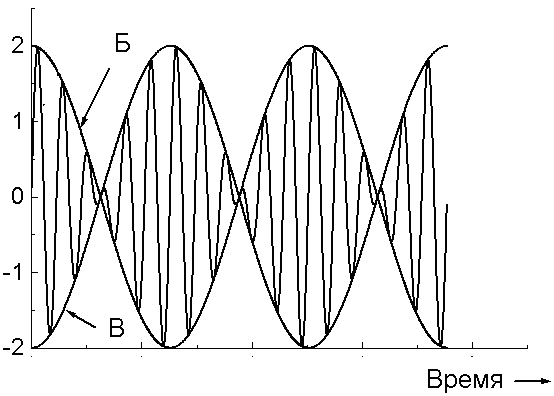
Гармоническое колебание совершается по закону косинуса с частотой ω0=1рад/с, начальной фазой φ0=0 и амплитудой А=1. Укажите график зависимости смещения от времени.
А |
Б |
В |
.
21. Гармоническое колебание совершается по закону косинуса с частотой ω0=2рад/с, начальной фазой φ0=0 и амплитудой А=1. Укажите график зависимости скорости от времени
1. А 2. Б. 3. В
|
|
22. Гармоническое колебание совершается по закону косинуса с частотой ω0=2рад/с, начальной фазой φ0=0 и амплитудой А=1. Укажите график зависимости смещения от времени.
1. А 2. Б . 3. В
|
|
23. Гармоническое колебание совершается по закону косинуса с частотой ω0=2рад/с, начальной фазой φ0=0 и амплитудой А=1. Укажите график зависимости ускорения от времени.
1. А 2. Б. 3. В
|
|
Свободные гармонические колебания совершаются
Под действием квазиупругой силы;
Под действием внешней периодически действующей силы;
Оба утверждения верны.
Между циклической частотой свободных гармонических колебаний и квазиупругой постоянной существует связь:
![]()
Период свободных гармонических колебаний пружинного маятника связан с квазиупругой постоянной соотношением:

Физическим маятником называется
Тело, совершающее колебания в поле тяжести Земли вокруг горизонтальной оси, не проходящей через центр тяжести;
Тело, совершающее колебания под действием внешней периодически действующей силы;
Материальная точка, подвешення не невесомой нерастяжимой нити и совершающая колебания в поле тяжести Земли.
Математическим маятником называется
Тело, совершающее колебания в поле тяжести Земли вокруг горизонтальной оси, не проходящей через центр тяжести;
Тело, совершающее колебания под действием внешней периодически действующей силы;
Материальная точка, подвешення не невесомой нерастяжимой нити и совершающая колебания в поле тяжести Земли.
При отклонении физического маятника на угол φ на него действует момент силы
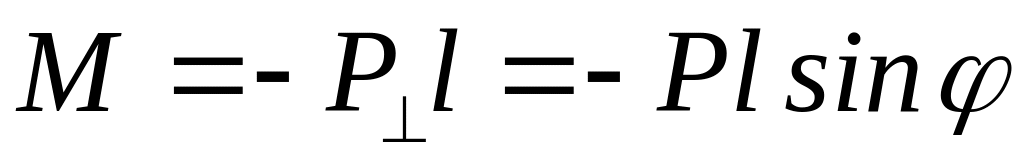 ,
где
,
гдеl – длина маятника;
l – плечо силы тяжести;
l – расстояние от центра тяжести до оси вращения.
Период колебаний физического маятника определяется формулой:

Период колебаний математического маятника определяется формулой:
Дифференциальное уравнение колебаний физического маятника имеет вид:

Гармоническое колебание совершается по закону
 .
Тогда потенциальная энергия такого
колебания имеет вид:
.
Тогда потенциальная энергия такого
колебания имеет вид:
![]()
Гармоническое колебание совершается по закону
 .
Тогда потенциальная энергия такого
колебания имеет вид:
.
Тогда потенциальная энергия такого
колебания имеет вид:
![]()
35. Гармоническое колебание совершается по закону . Тогда кинетическая энергия такого колебания имеет вид:
![]()
36. Гармоническое колебание совершается по закону . Тогда кинетическая энергия такого колебания имеет вид:
![]() 37.
Полная энергия гармонического колебания
имеет вид:
37.
Полная энергия гармонического колебания
имеет вид:
![]()
:
38. Гармоническое колебание совершается по закону. . Тогда кинетическая энергия такого колебания имеет вид, изображённый на графике: 1. А;
2.Б;
3.В
|
|
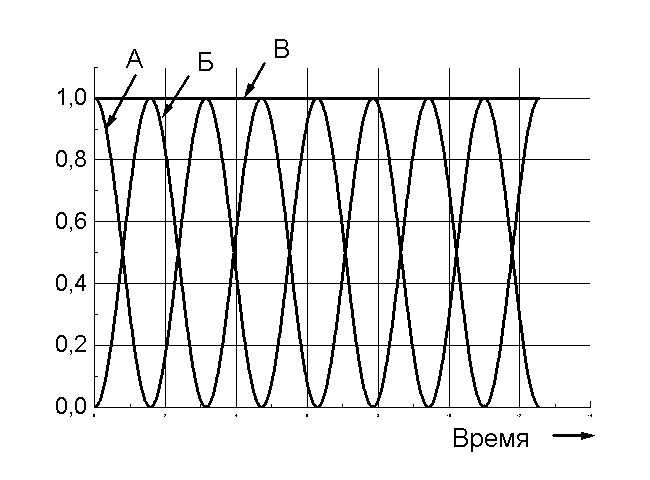
39. Гармоническое колебание совершается по закону. . Тогда потенциальная энергия такого колебания имеет вид, изображённый на графике: 1. А;
2.Б;
3.В
|
|
39. Гармоническое колебание совершается по закону. . Тогда полная механическая энергия такого колебания имеет вид, изображённый на графике: 1. А;
2.Б;
3.В
|
|
40. Гармоническое колебание совершается по закону. . Тогда кинетическая энергия такого колебания имеет вид, изображённый на графике: 1. А;
2.Б;
3.В
|
|
.
41. Гармоническое колебание совершается по закону. . Тогда потенциальная энергия такого колебания имеет вид, изображённый на графике: 1. А;
2.Б;
3.В
|
|
42. При сложении двух скалярных гармонических колебаний одинаковой частоты результирующая амплитуда колебаний находится по формуле:

43. Складываются два гармонических колебания с одинаковой частотой и одинаковой фазой. При этом результирующая амплитуда колебаний находится по формуле:
![]()
44. Складываются два гармонических колебания с одинаковой частотой и противоположной фазой. При этом результирующая амплитуда колебаний находится по формуле:
45. Складываются два гармонических колебания с одинаковой частотой и противоположной фазой. При этом результирующее смещение имеет вид, изображённый на графике:
|
|
46. Складываются два гармонических колебания с одинаковой частотой и одинаковой фазой. При этом результирующее смещение имеет вид, изображённый на графике:
1. А;
2. Б;
3. В. |
|
47. Необходимыми условиями для возникновения биений являются:
1. Амплитуды одинаковы; частоты одинаковы; начальные фазы одинаковы;
2.Амплитуды близкие по значению; частоты одинаковы; начальные фазы одинаковы;
3.Амплитуды одинаковы; частоты близкие по значению; начальные фазы одинаковы.
48. Период биений определяется формулой:
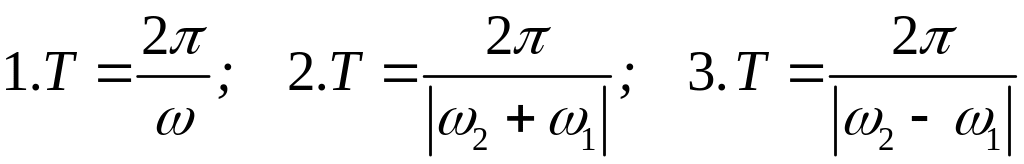
49. Укажите кривую зависимости смещения от времени в процессе биений
1. Б;
2. А;
3. В.
|
|
50. Укажите кривую зависимости амплитуды от времени в процессе биений
1. Б;
2. В;
3. Оба ответа верны.
|
|
51. Складываются два взаимно перпендикулярных гармонических колебания с одинаковой частотой. При этом результирующее движение описывается уравнением:

52. При сложении двух взаимно перпендикулярных гармонических колебаний с одинаковой частотой результирующее движение описывается уравнением:

При этом смещение x изменяется в пределах:
1. От 0 до А1; 2. от – А1 до + А1; 3. от – ( А1+А2)/2 до +( А1+А2)/2.
53. При сложении двух взаимно перпендикулярных гармонических колебаний с одинаковой частотой результирующее движение описывается уравнением:
При этом смещение у изменяется в пределах:
1. От 0 до А2; 2. от – А2 до + А2; 3. от – ( А1+А2)/2 до +( А1+А2)/2.
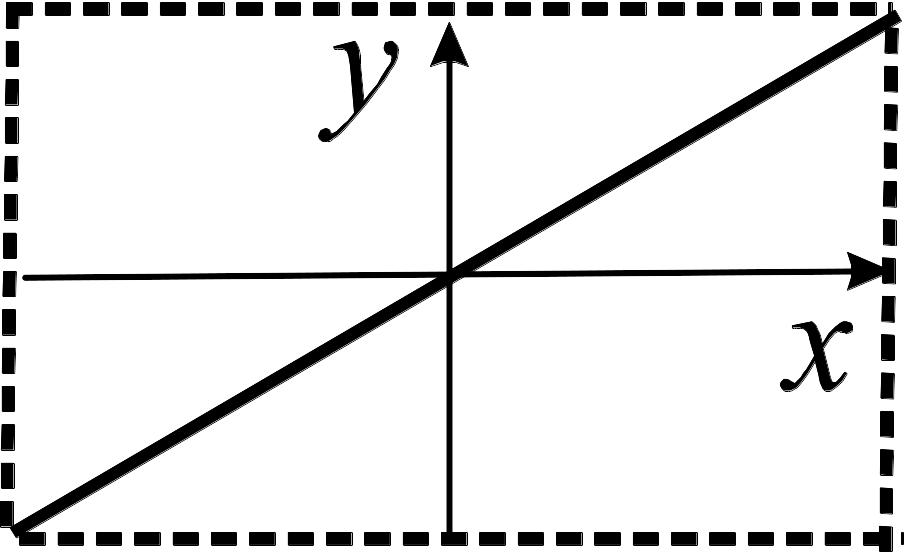
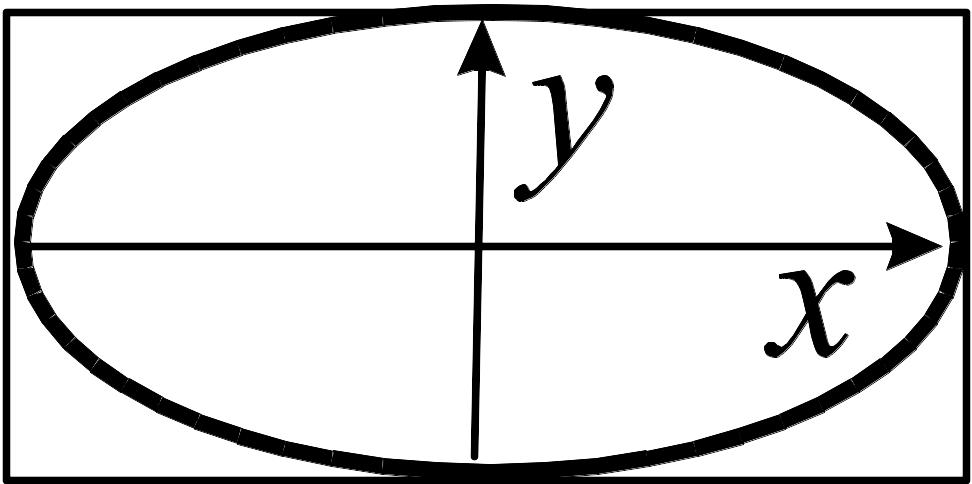
54. Укажите условия, при которых получается фигура Лиссажу, показанная на рисунке: 1. Частоты складываемых колебаний равны; начальные фазы совпадают. 2. Частоты складываемых колебаний равны; начальные фазы противоположны. 3. Частоты складываемых колебаний равны; начальные фазы отличаются на π/2. |
|
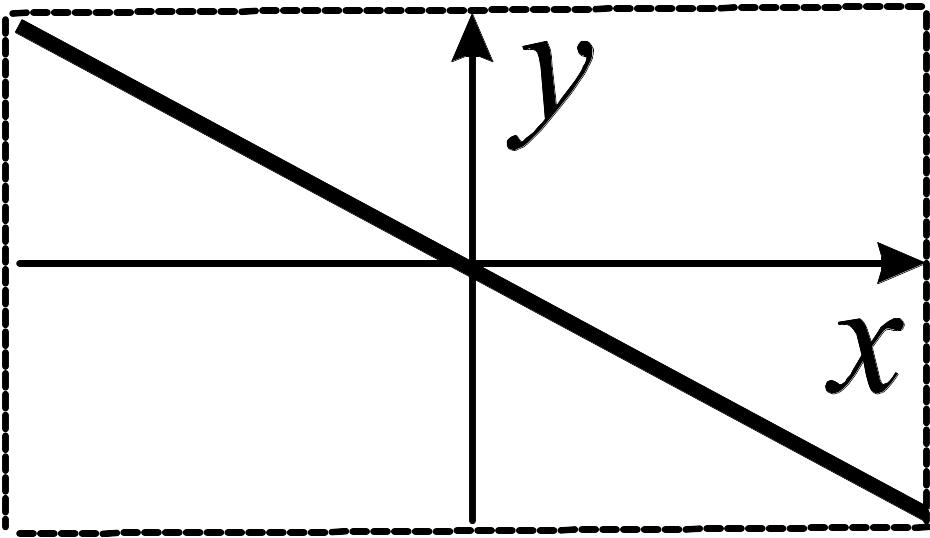
55. Укажите условия, при которых получается фигура Лиссажу, показанная на рисунке: 1. Частоты складываемых колебаний равны; начальные фазы совпадают. 2. Частоты складываемых колебаний равны; начальные фазы противоположны. 3. Частоты складываемых колебаний равны; начальные фазы отличаются на π/2. |
|
56. Укажите условия, при которых получается фигура Лиссажу, показанная на рисунке: 1. Частоты складываемых колебаний равны; начальные фазы совпадают. 2. Частоты складываемых колебаний равны; начальные фазы противоположны. 3. Частоты складываемых колебаний равны; начальные фазы отличаются на π/2. |
|
57. Складываются два взаимно перпендикулярных
колебания
![]() .
При этом фигура Лиссажу будет иметь вид
.
При этом фигура Лиссажу будет иметь вид
1. прямой, проходящей через первый и третий квадранты;
2. прямой, проходящей через второй и четвёртый квадранты;
3. окружности.
58. Складываются два взаимно перпендикулярных
колебания
![]() .
При этом фигура Лиссажу будет иметь вид
.
При этом фигура Лиссажу будет иметь вид
1. прямой, проходящей через первый и третий квадранты;
2. прямой, проходящей через второй и четвёртый квадранты;
3. окружности.
59. Складываются два взаимно перпендикулярных
колебания
![]() .
При этом фигура Лиссажу будет иметь вид
.
При этом фигура Лиссажу будет иметь вид
1. прямой, проходящей через первый и третий квадранты;
2. прямой, проходящей через второй и четвёртый квадранты;
3. окружности.
60. Складываются два взаимно перпендикулярных
колебания
![]() .
При этом фигура Лиссажу будет иметь вид
.
При этом фигура Лиссажу будет иметь вид
1. прямой, проходящей через первый и третий квадранты;
2. прямой, проходящей через второй и четвёртый квадранты;
3. эллипса.
61. Складываются два взаимно перпендикулярных
колебания
![]() .
При этом фигура Лиссажу будет иметь вид
.
При этом фигура Лиссажу будет иметь вид
1. прямой, проходящей через первый и третий квадранты;
2. прямой, проходящей через второй и четвёртый квадранты;
3. эллипса.
62. Складываются два взаимно перпендикулярных
колебания
![]() .
При этом фигура Лиссажу будет иметь вид
.
При этом фигура Лиссажу будет иметь вид
1. прямой, проходящей через первый и третий квадранты;
2. прямой, проходящей через второй и четвёртый квадранты;
3. эллипса.
63. Затухающие колебания совершаются под действием
1. силы сопротивления
![]()
2. квазиупругой силы
![]()
3.совместного действия квазиупругой
силы и силы сопротивления![]()
64. Затухающие колебания совершаются по
закону
![]() ,
где
,
где

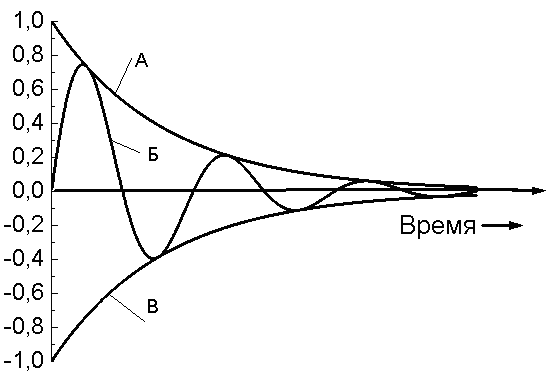
65. На рисунке приведен график затухающих колебаний. Укажите, какая из кривых соответствует смещению, амплитуде:
Смещение Амплитуда 1. Б А
2. А Б
3. В А |
|
66. Амплитуда затухающих колебаний изменяется по закону:
![]()
67. Логарифмический декремент затухания равен
1. частоте затухающих колебаний;
2. периоду затухающих колебаний;
3. логарифму отношению амплитуд, взятых через промежуток времени, равному периоду колебаний.
68. Логарифмический коэффициент затухания связан с периодом колебаний Т и коэффициентом затухания β соотношением:
![]()
69. На рисунке показана зависимость амплитуды колебаний от времени для трёх затухающих колебаний с различными коэффициентами затухания β1, β2, β3. Укажите правильное соотношение между этими значениями.
|
|
70. На рисунке показана зависимость амплитуды колебаний от времени для трёх затухающих колебаний с различными значениями логарифмического декремента затухания λ1, λ 2, λ 3. Укажите правильное соотношение между этими значениями.
|
|
71. На рисунке показан график зависимости смещения от времени для системы, совершающей затухающие колебания. Это 1. случай апериодического движения, когда сила сопротивления превышает квазиупругую силу.
2. случай апериодического движения,
когда
3. случай апериодического движения,
когда
|
|
72. Добротность системы определяет потери механической энергии на преодоление сил сопротивления за время, равное периоду колебаний. При этом
1. Чем выше добротность, тем меньше потери;
2. Чем выше добротность, тем больше потери.
3. Оба ответа неправильны.
73. Добротность системы можно определить по формуле:
1. ,
где
,
где
![]() – потери механической энергии на
преодоление сил сопротивления за время,
равное периоду колебаний
– потери механической энергии на
преодоление сил сопротивления за время,
равное периоду колебаний
2.
![]() ,
где λ – логарифмический декремент
затухания.
,
где λ – логарифмический декремент
затухания.