5.Основные определения статистики Максвелла

1. Распределение Максвелла – это распределение частиц по

1) потенциальным энергиям;

2) скоростям;

3) полной механической энергии.

2. Функция распределения Максвелла определяет

1) абсолютное число частиц, имеющих скорости в интервале от до ;

2) абсолютное число частиц, имеющих энергии в интервале от до ;

3) относительное число частиц, имеющих скорости в интервале от до .

3. Функция распределения Максвелла определяет

1) абсолютное число частиц, имеющих скорости в интервале от до ;

2) относительное число частиц, имеющих скорости в интервале от до ;

3) относительное число частиц, имеющих скорости в единичном интервале.

4. Функция распределения Максвелла определяет

1) абсолютное число частиц, имеющих скорость ;

2) относительное число частиц, имеющих скорость ;

3) относительное число частиц, имеющих скорость в интервале от до .

5. Функция распределения Максвелла определяет

1) абсолютное число частиц, имеющих скорости в интервале от до ;

2) число частиц в единичном объёме, имеющих скорости в интервале от до ;

3) относительное число частиц, имеющих скорости в интервале от до .

6. Функция распределения Максвелла определяется выражением

1) ; 2) ; 3) .

7. При данной температуре наибольшее число молекул имеют скорость вблизи

1) средней скорости;

2) среднеквадратичной скорости;

3) наиболее вероятной скорости.

8. Наиболее вероятная скорость молекул это

1) среднее значение всех скоростей молекул;

2) среднее значение модулей всех скоростей молекул;

3) скорость, близкую к которой имеет максимальное количество молекул.

9. Среднеквадратичная скорость это

1) квадрат от средней скорости молекул;

2) корень квадратный от среднего квадрата скоростей молекул;

3) наиболее вероятная скорость в квадрате.

10. Средняя скорость молекул это

1) скорость, которую имеют большинство молекул;

2) среднее значение модулей скоростей всех молекул;

3) оба утверждения верны.

11. Среднеквадратичная скорость молекул газа при данном давлении зависит от

1) температуры;

2) объёма;

3) оба утверждения верны.

12. В данном объёме при данной температуре Т скорости молекул

1) одинаковы;

2) лежат в интервале ;

3) могут быть любыми.

13. Среднеквадратичная скорость молекул кислорода на уровне моря была 500 м/с. Какой стала среднеквадратичная скорость на высоте 5 км? (Считать температуру постоянной).

1) 372 м/с 2) 500 м/с; 3) 813 м/с.

14. График функции распределения Максвелла изображён на рисунке

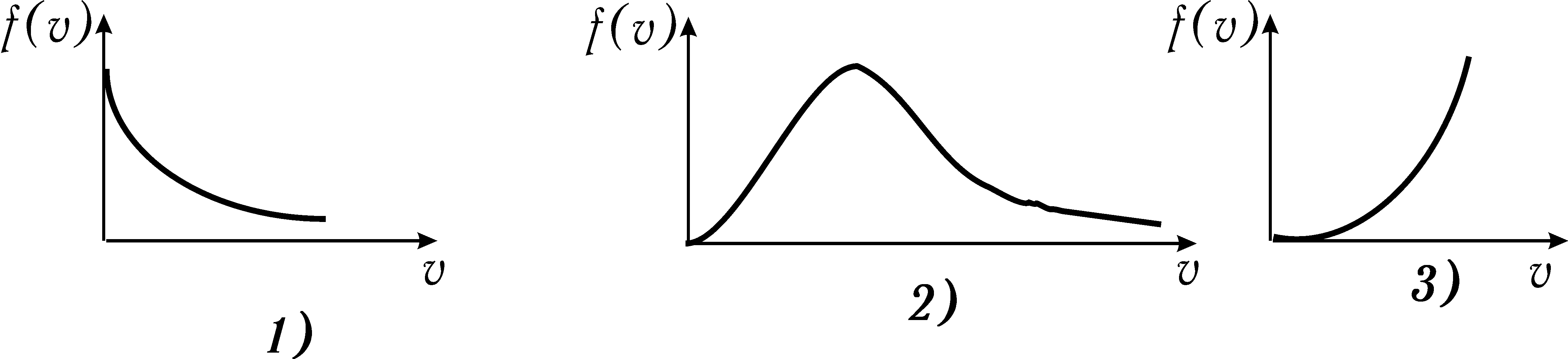
15. Функция распределения Максвелла для двух температур указана правильно на рисунке

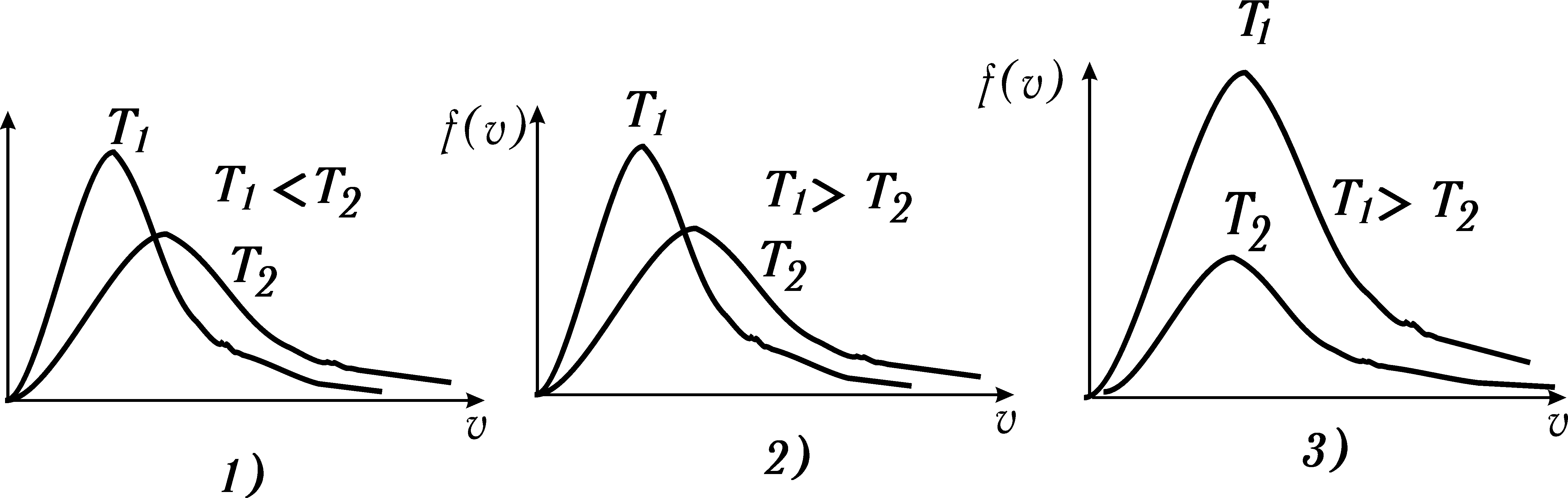
16. Н 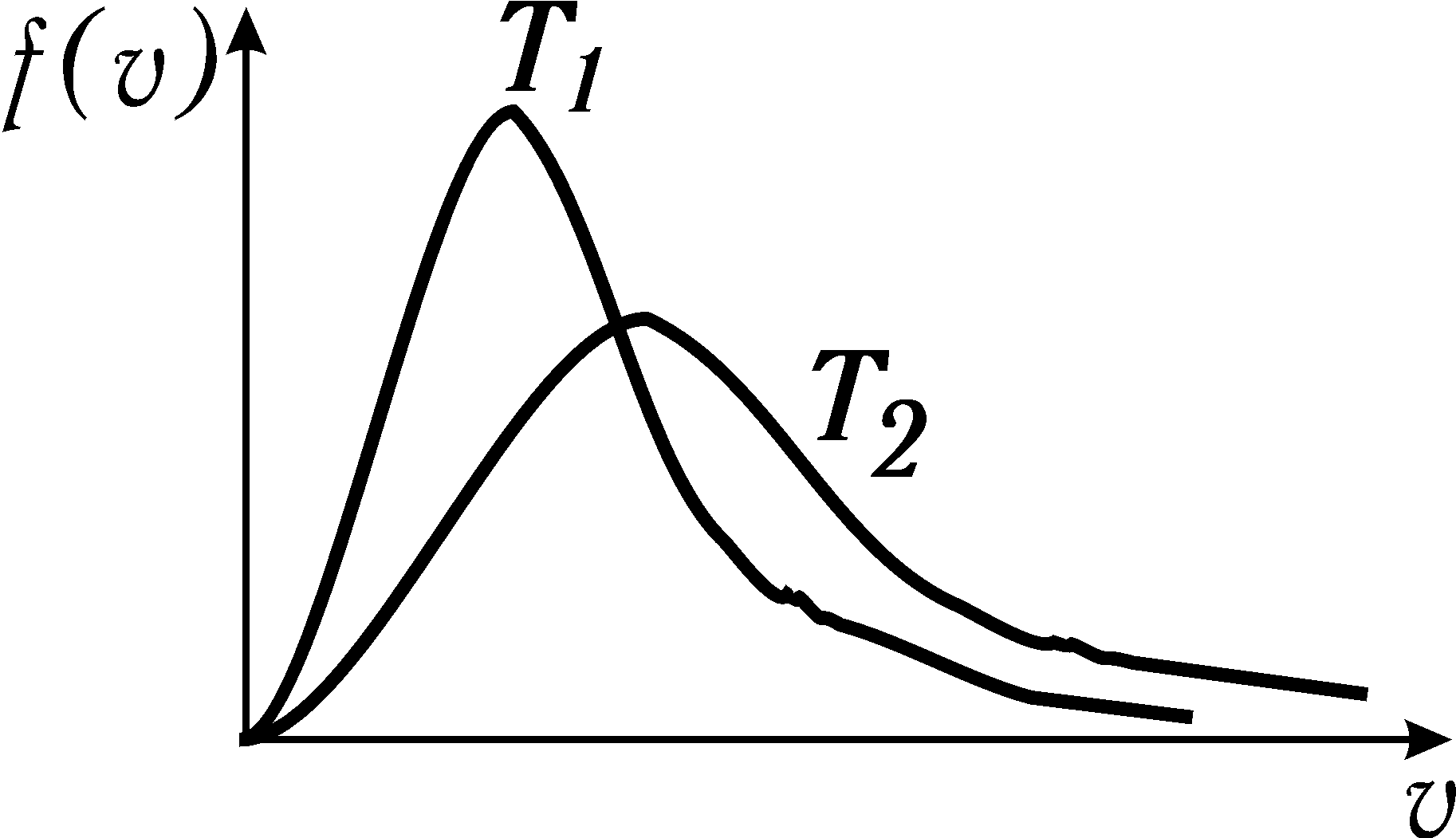а рисунке показаны кривые распределения Максвелла при двух температурах. Как соотносятся температуры?

а) ;

б) ;

в) .

17. Площадь заштрихованной фигуры на графике определяет

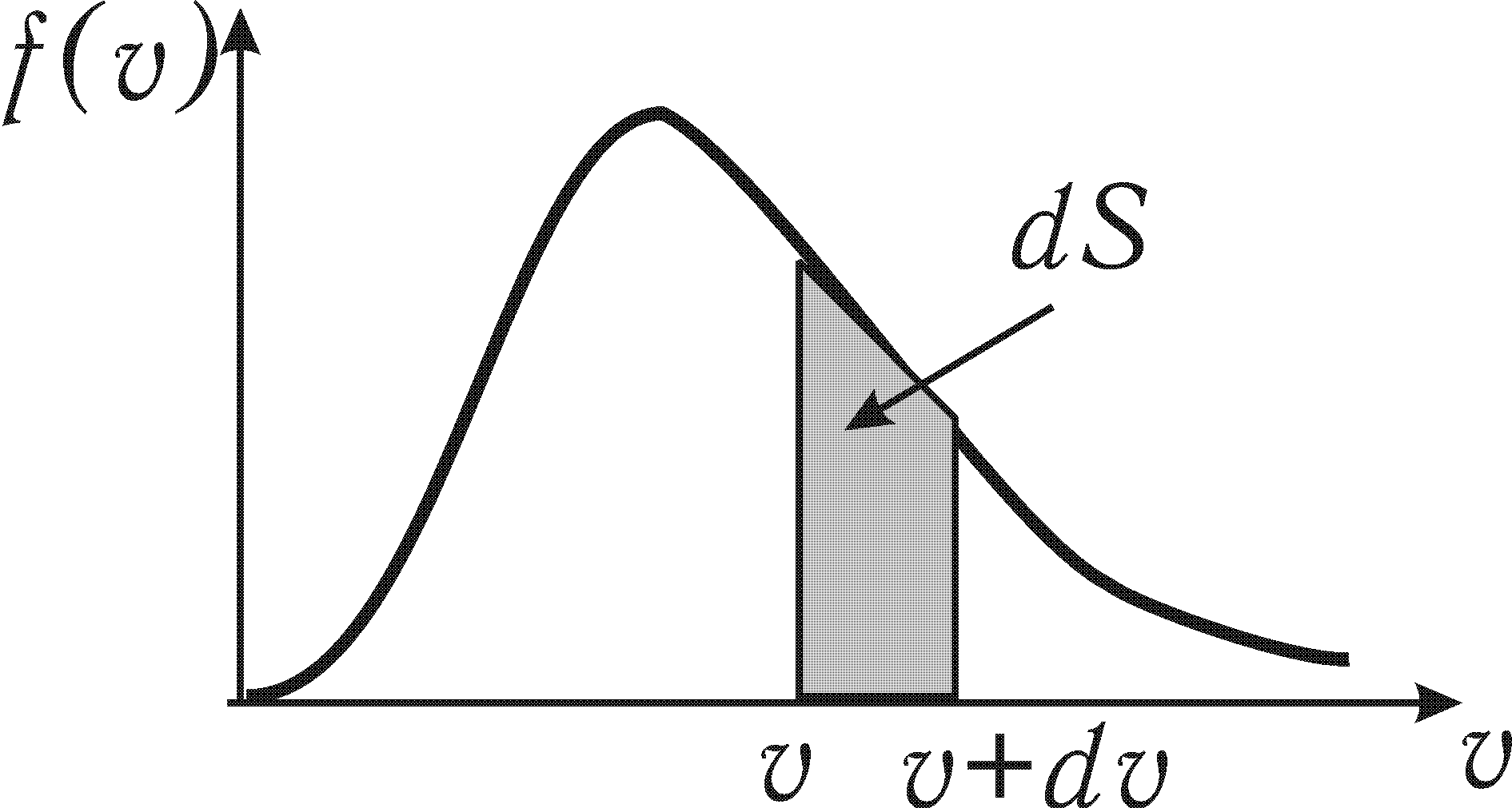
1) абсолютное число частиц, имеющих скорости в интервале от до ;

2) число частиц в единичном объёме, имеющих скорости в интервале от до ;

3) относительное число частиц, имеющих скорости в интервале от до .

18. Условие нормирования функции распределения Максвелла выглядит как

1) ; 2) ; 3) .

19. Площадь под кривой от функции распределения Максвелла равна

1) единице;

2) числу молекул газа;

3) числу молекул в единице объёма газа.

20. При увеличении температуры площадь под кривой функции распределения Максвелла

1) увеличивается;

2) уменьшается;

3) остаётся постоянной.

21. Наиболее вероятная скорость находится из выражения

1) ; 2) ; 3) .

22. Средняя скорость молекул газа находится из выражения

1) ; 2) ; 3) .