3. Обе формулы верны.

93. Громкость звука определяется

1. интенсивностью (силой) звука;

2. частотой;

3. формой звуковых колебаний.

94. Высота звука определяется

1. интенсивностью (силой) звука;

2. частотой;

3. формой звуковых колебаний.

95. Тембр звука определяется

1. интенсивностью (силой) звука;

2. частотой;

3. формой звуковых колебаний.

96. На рисунке показан случай движения приёмника навстречу источника звука. При этом приёмник регистрирует частоту:
1. ; 2. ; 3.

97. На рисунке показан случай, когда приёмник удаляется от источника звука. При этом приёмник регистрирует частоту:
1. ; 2. ; 3.

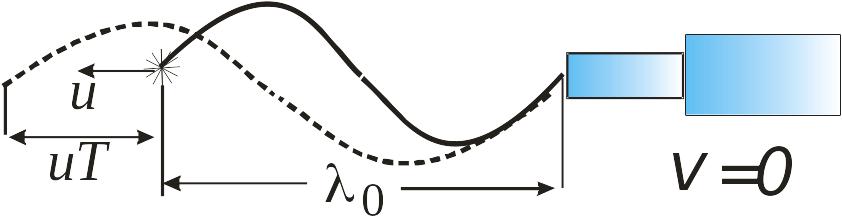
98. На рисунке показан случай, когда источник звука приближается к приёмнику. При этом приёмник регистрирует частоту:
1. ; 2. ; 3.

99. На рисунке показан случай, когда источник звука удаляется от приёмника. При этом приёмник регистрирует частоту:
1. ; 2. ; 3.

Задачи

100. Амплитуда вынужденных колебаний зависит от частоты внешней периодически действующей силы ω по формуле:

Исходя из этой формулы, покажите, что резонансная частота определяется выражением:

.

101. Гармоническое колебание совершается по закону . Чему равна скорость в момент времени t=0?

1). ; 2). 3/2; 3). 2.

102. Гармоническое колебание совершается по закону . Чему равна скорость в момент времени t=0?

1). ; 2). – ; 3). 2.

103. Гармоническое колебание совершается по закону . Чему равно ускорение в момент времени t=0?

1). ; 2). 3/2; 3). .

104. Гармоническое колебание совершается по закону . Чему равен период колебаний?

1). ; 2). ; 3). 2.

105. Гармоническое колебание совершается по закону . Чему равен период колебаний?

1). ; 2). ; 3). 1.

106. Пружинный маятник массой m=100 г совершает гармонические колебания с частотой ω₀ = 30 рад/с. Чему равна жёсткость пружины?

1. 90 Н/м; 2. 30 Н/м; 3. 45 Н/м.

107. На пружине жёсткостью к= 1 кН/м укреплён груз массой m= 1 кг. Чему равен период колебаний такого пружинного маятника?

1. 6.28 с; 2. 1 с; 3. 3.14 с.

108. Определить возвращающую силу F в момент времени t=1/8 c точки массой m=20 г, совершающей гармонические колебания согласно уравнению , где А=15 см, ω=4 с^-1.

1. -1.43 Н; 2. 1.43 Н; 3. 0.

109. Определить потенциальную энергию W­p в момент времени t=1/8 c точки массой m=20 г, совершающей гармонические колебания согласно уравнению , где А=15 см, ω=4 с^-1.

1. 0.214 Дж; 2. 0.107 Дж. 3.0.

110. Определить кинетическую энергию W_к в момент времени t=1/8 c точки массой m=20 г, совершающей гармонические колебания согласно уравнению , где А=15 см, ω=4 с^-1.

1. 0.214 Дж; 2. 0.107 Дж. 3.0.

111. Определить полную энергию точки массой m=20 г, совершающей гармонические колебания согласно уравнению , где А=20 см, ω=4 с^-1.

1. 3.14·10 ^-2 Дж; 2. 6.31·10² Дж; 3. 5.14·10² Дж;

112. Определить максимальную скорость материальной точки, совершающей гармонические колебания согласно уравнению , где А= 2 см, ω= 3 с^-1.

1. 6·10 ^-2 м/с; 2. 3·10 ^-2 м/с; 3. 1.5·10 ^-2 м/с.

113. Определить максимальное по модулю ускорение материальной точки, совершающей гармонические колебания согласно уравнению , где А= 2 см, ω= 3 с^-1.

1. 0.18 м/с²; 2. 0.36 м/с²; 3. 0.72 м/с² .

114. Материальная точка совершает гармонические колебания согласно уравнению , где ω=2 с^-1. В какой момент времени смещение равно половине амплитуды?

1. 0.13 с. 2. 0.52 с. 3. 0.26 с.

115. Материальная точка совершает гармонические колебания согласно уравнению , где ω=2 с^-1. В какой момент времени смещение равно значения амплитуды?

1. 0.13 с. 2. 0.52 с. 3. 0.26 с.

116. На пружине жёсткостью к= 4 кН/м укреплён груз массой m= 1 кг. Напишите уравнение колебаний такого пружинного маятника, если амплитуда колебаний А= 2 см.

1). x=0.02 cos2t; 2) x=0.02 cos4t; 3) x=0.02 cost.

117. Материальная точка совершает гармонические колебания согласно уравнению , где ω=2 с^-1. В какой момент времени смещение равно значения амплитуды?

1. 0.13 с. 2. 0.52 с. 3. 0.39 с.

118. Материальная точка совершает гармонические колебания с периодом Т=4 с. В некоторый момент времени смещение максимально. Через какой промежуток времени Δt скорость достигнет максимального значения?

1) 1 c; 2) 2 c; 3) 4 с.

119. Материальная точка совершает гармонические колебания с периодом Т=4 с. В некоторый момент времени скорость максимальна. Через какой промежуток времени Δt ускорение достигнет максимального значения?

1) 1 c; 2) 2 c; 3) 4 с.

120. Материальная точка совершает гармонические колебания с периодом Т=4 с. В некоторый момент времени ускорение максимально. Через какой промежуток времени Δt скорость достигнет максимального значения?

1) 1 c; 2) 2 c; 3) 4 с.

121. Материальная точка совершает гармонические колебания с амплитудой А. При каких значениях смещения х скорость максимальна?

1) х = 0; 2) х = А; 3) х = А/2.

122. Материальная точка совершает гармонические колебания с амплитудой А. При каких значениях смещения х ускорение максимально?

1) х = 0; 2) х = А; 3) х = А/2.

123. Материальная точка совершает гармонические колебания с амплитудой А. При каких значениях смещения х ускорение и скорость одновременно достигают максимального значения?

1) х = 0; 2) х = А; 3) Такое состояние не реализуется.

124. Материальная точка совершает гармонические колебания с периодом Т=4 с.. В некоторый момент времени кинетическая энергия максимальна. Через какой промежуток времени потенциальная энергия достигнет максимального значения?

1) 2 c; 2) 1 c; 3) 4 с.

125. Найти максимальную кинетическую энергию материальной точки массой m=2 г, совершающей гармонические колебания с амплитудой А= 4 см и частотой .

1) 0.04 мДж; 2) 3.16 мДж; 3) 1.58 мДж.

126. Точка совершает гармонические колебания. В некоторый момент времени смещение точки x=5 см и модуль ускорения │a│= 80 см/с². Найти циклическую частоту колебаний ω.

1) 4 с^-1; 2) 16 с^-1; 3) 8 с^-1.

127. Точка совершает гармонические колебания c частотой ω = 10 с^-1. В некоторый момент времени смещение точки x=4 см и модуль скорости │v│= 30 см/с². Найти амплитуду колебаний. Указание: воспользуйтесь тождеством .

1) 3 см; 2) 5 см; 3) 4 см.

128. Материальная точка массой m= 100 г совершает гармонические колебания, уравнение которых имеет вид x=A·sinωt, где А=5 см, ω =2с^-1. В какой момент времени (ближайший к началу отсчёта) возвращающая сила F= –10^-2 Н?

1) π/3; 2) π/6; 3) π/12.

129. Два гармонических колебания, направленных вдоль одной прямой, имеющих одинаковые амплитуды и периоды, складываются в одно колебание той же амплитуды. Найти разность фаз складываемых колебаний.

1) 60⁰; 2) 90⁰; 3) 120⁰.

130. Точка совершает одновременно два гармонических колебания, происходящих во взаимно перпендикулярным направлениям и выражаемых уравнениями: и , где А₁= 4 см, ω₁ = π с^-1; А₂= 8 см, ω₂=π с^-1, τ=1 с. Найти уравнение траектории.

1. .

131. Точка совершает одновременно два гармонических колебания, происходящих вдоль одной прямой и выражаемых уравнениями: и , где А₁= 4 см, А₂ = 8 см, ω = π с^-1, τ = 1 с. Найти результирующую амплитуду колебаний.

1) 6 см; 2) 4 см; 3) см.

132. Точка совершает одновременно два гармонических колебания, происходящих вдоль одной прямой и выражаемых уравнениями: и , где А₁= 4 см, А₂=3 см, ω=π с^-1, τ=0.5 с. Найти результирующую амплитуду колебаний

1) 1 см; 2) 7 см; 3) 5 см.

133. Точка совершает одновременно два гармонических колебания, происходящих вдоль одной прямой и выражаемых уравнениями: и , где А₁= 4 см, А₂=3 см, ω=π с^-1, τ =1/3 с. Найти результирующую амплитуду колебаний

1) 31 см; 2) 7 см; 3) 1 см.

134. Точка совершает одновременно два гармонических колебания, происходящих вдоль одной прямой и выражаемых уравнениями: и , где А₁= 4 см, А₂=3 см, ω=π с^-1, τ =1/6 с. Найти результирующую амплитуду колебаний

1) 5 см; 2) 5.9 см; 3) 7 см.

135. Точка совершает одновременно два гармонических колебания, происходящих во взаимно перпендикулярным направлениям и выражаемых уравнениями: и , где А₁= 4 см, ω₁ = π с^-1; А₂= 8 см, ω₂=π с^-1, τ=0. Найти уравнение траектории.

1) ; 2) ; 3) .

136. Точка совершает одновременно два гармонических колебания, происходящих во взаимно перпендикулярным направлениям и выражаемых уравнениями: и , где А₁= 4 см, ω₁ = π с^-1; А₂= 8 см, ω₂=π с^-1, τ = 0.5 с. Найти уравнение траектории.

1) .

137. Точка совершает одновременно два гармонических колебания, происходящих во взаимно перпендикулярным направлениям и выражаемых уравнениями: . Найти траекторию движения точки.

.

138. Найти линейную частоту колебаний груза массой 400 г, подвешенного к пружине жёсткостью 160 Н/м.

1) 3.2 Гц; 2) 20 Гц; 3) 400 Гц.

139. Найти массу груза, который на пружине с жёсткостью 250 Н/м делает 20 колебаний за 16 с.

1) 3 кг; 2) 4 кг; 3) 5 кг.

140. Во сколько раз изменится частота колебаний автомобиля на рессорах после принятия груза, равного массе порожнего автомобиля?

1) увеличится в раза; 2) не изменится; 3) уменьшится в раза.

141. Шарик, подвешенный на тонкой нерастяжимой нити, совершал колебания с периодом Т. Во сколько раз изменится период колебаний, если отрезать ¾ длины нити и подвесить на оставшуюся часть тот же шарик.

1) увеличится в 2 раза; 2) не изменится; 3) уменьшится в 2 раза.

142. Груз массой 1 кг, подвешенный к пружине с жёсткостью 100Н/м, совершает колебания с амплитудой 10 см. Написать уравнение движения груза.

1)

143. Чему равно ускорение свободного падения, если математический маятник длиной 80 см совершил за 3 мин 100 колебаний?

1) 9.81 м/с²; 2) 9 .74 м/с²; 3) 9.78 м/с².

144. Как относятся длины математических маятников, если за одно и то же время один из них совершает 10, а второй 30 колебаний?

1) 3:1; 2) 1:3; 3) 9:1.

145. За одно и то же время один математический маятник делает 50 колебаний, а второй 30. Найти их длины, если один из них на 32 см короче другого.

1) l₁=50 cм, l₂ =18 cм; 2) l₁=60 cм, l₂ =28 cм; 3 l₁=40 cм, l₂ =8 cм.

146. Груз совершает колебания на пружине жёсткостью k = 250 Н/м. Амплитуда колебаний A = 15 см. Найти полную механическую энергию колебаний.

1) 1.4 Дж; 2) 2.8 Дж; 3) 4.2 Дж.

147. Во сколько раз изменилась полная механическая энергия математического маятника при уменьшении длины в 3 раза и увеличении амплитуды в 2 раза?

1) увеличилась в 12 раз; 2) уменьшилась в 12 раз; увеличилась в 6 раз.

148.Груз, подвешенный на пружине с жёсткостью k = 1кН/м, колеблется с амплитудой A=2 см. Найти кинетическую W_k и потенциальную W_p энергию при фазе π/3 рад. Указание: для однозначности ответа выразите уравнение движения через косинус.

1) W_k=50 мДж , W_p=150 мДж ;

2) W_k=150 мДж , W_p=50 мДж ;

3) W_k=120мДж , W_p=80 мДж ;

149. Пружинный маятник вывели из положения равновесия и отпустили. Через какое время (в долях периода) кинетическая энергия колеблющегося тела будет равна потенциальной энергии пружины?

1) Т/2; 2) Т/4; 3) Т/8.

150. Частица массой m = 0.01 кг совершает гармонические колебания с периодом Т = 2 с. Полная энергия колеблющейся частицы W=0.1 мДж. Определить амплитуду А колебаний.

1) 45 мм; 2) 54 мм; 3) 24 мм.

151. Материальная точка участвует одновременно в двух взаимно перпендикулярных гармонических колебаниях, уравнения которых: , где А₁=1 см, ω₁=π с^-1; А₂=2 см, ω₁=π/2 с^-1. Найти уравнение траектории точки.

1) 2) 3)

152. Определить частоту гармонических колебаний диска радиусом R=20 см около горизонтальной оси, проходящей через середину радиуса диска перпендикулярно его плоскости. Справка: собственный момент диска .

1) 0.76 Гц; 2) 0.98 Гц; 3) 0.67 Гц.

153. Определить частоту гармонических колебаний диска радиусом R =20 см около горизонтальной оси, проходящей через обод диска перпендикулярно его плоскости. Справка: собственный момент диска .

1) 0.51 Гц; 2) 0.61 Гц; 3) 0.71 Гц;

154. Определить частоту гармонических колебаний стержня длиной l=20 см около горизонтальной оси, отстоящей от середины стержня на расстоянии l/4 и расположенной перпендикулярно его плоскости. Справка: собственный момент стержня .

1) 1.46 Гц; 2) 3.86 Гц; 3) 2.26 Гц.

155. Определить частоту гармонических колебаний стержня длиной l=20 см около горизонтальной оси, проходящей через конец стержня перпендикулярно его плоскости. Справка: собственный момент стержня .

1) 1.56 Гц; 2) 1.46 Гц; 3) 1.36 Гц.

156. Определить частоту гармонических колебаний шара радиусом R=20 см около горизонтальной оси, отстоящей от центра шара на расстоянии 2R. Справка: собственный момент шара .

1) 0.92 Гц; 2) 0.62 Гц; 3) 0.32 Гц.

157. Через время, равное периоду колебаний Т = 2 с, амплитуда затухающих колебаний уменьшилась в 2 раза. Определить логарифмический декремент затухания λ и коэффициент затухания β.

1) λ= 0.301, β=0.15 с^-1; 2) λ= 0.693, β=0.346 с^-1; 3) λ= 1, β=0.5 с^-1.

158. Амплитуда затухающих колебаний убывает по закону . Частота колебаний =2 Гц. Определить логарифмический декремент затухания λ.

1) 0.25; 2) 0.5; 3) 0.75.

159. Амплитуда затухающих колебаний убывает по закону . Частота колебаний =2 Гц. Определить логарифмический декремент затухания λ и добротность Q.

1) λ =0.5, Q=6.28; 2) λ =0.25, Q=12.56 ; 3) λ =0.75, Q=4.19.

160. Затухающие колебания описываются уравнением , где β=2 с^-1, ω=12 с^-1. Определить логарифмический декремент затухания λ и добротность Q.

1) λ =0.5, Q=6.28; 2) λ =1.05, Q=3; 3) λ =0.75, Q=4.19.

161. Затухающие колебания описываются уравнением , где β=2 с^-1, ω=10 с^-1. Определить логарифмический декремент затухания λ и добротность Q.

1) λ =0.5, Q=6.28; 2) λ =0.17, Q=18.5; 3) λ =1.26, Q=2.5.

162. В некоторый момент времени полная механическая энергия системы, совершающей затухающие колебания, была W₁= 2 мДж. Через время, равное периоду колебаний, энергия системы стала равной W₂= 1.95 мДж. Определить добротность системы Q и логарифмический коэффициент затухания λ.

1) Q =40 , λ =7.85· 10^-2 ; 2) Q =50 , λ = 6.28· 10^-2; 3) Q =80 , λ =3.92 · 10^-2 .

163. Внутри системы массой m=1 кг, совершающей затухающие колебания, действуют квазиупругая сила и сила сопротивления , где . Напишите дифференциальное уравнение затухающих колебаний.

1)

2)

3)

164. Внутри системы массой m=2 кг, совершающей затухающие колебания, действуют квазиупругая сила и сила сопротивления , где . Напишите дифференциальное уравнение затухающих колебаний.

1)

2)

3)

165. Внутри системы массой m=0.2 кг, совершающей затухающие колебания, действуют квазиупругая сила и сила сопротивления , где . Напишите дифференциальное уравнение затухающих колебаний.

1)

2)

3)

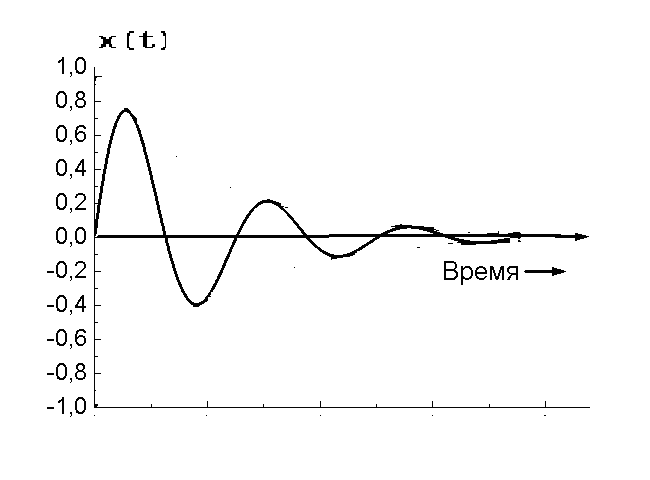
166. Какой вид будет иметь решение дифференциального уравнения затухающих колебаний

1) а; 2) б; 3) в.

а	б	в

167. Какой вид будет иметь решение дифференциального уравнения затухающих колебаний

1) а; 2) б; 3) в.

а	б	в

168. Определить максимальное ускорение материальной точки, совершающей гармонические колебания с амплитудой А=15 см, если наибольшая скорость точки

!) 60 см/с²; 2) 30 см/с²; 3) 120 см/с².

169. Определить циклическую частоту гармонических колебаний, если максимальное ускорение , а максимальная скорость

1) ω=4 с^-1; 2) ω=2 с^-1; 3) ω=6 с^-1.

170. Найти максимальную кинетическую энергию материальной точки массой m=2г, совершающей гармонические колебания с амплитудой А= 4 см и частотой =5 Гц.

1) 2,28 мДж; 2) 3,28 мДж; 3) 1,58 мДж.

171. Найти максимальную потенциальную энергию материальной точки массой m=2г, совершающей гармонические колебания с амплитудой А= 4 см и частотой ω=50 Гц.

1) 0,4 мДж; 2) 1,4 мДж; 3) 2,4 мДж.

172. Складываются два колебания одинакового направления и одинакового периода: . Найти амплитуду А_р результирующего колебания.

1) 6 см; 2) см; 3) см.

173. Складываются два колебания одинакового направления и одинакового периода: . Найти амплитуду А_р результирующего колебания.

1) 6 см; 2) см; 3) 0.

174. Складываются два колебания одинакового направления и одинакового периода: . Найти амплитуду А_р результирующего колебания

1) 0; 2) см; 3) 6 см;

175. Две точки находятся на прямой, вдоль которой распространяются волны со скоростью v=10 м/с. Период колебаний Т=0.2 с, расстояние между точками Δx=1 м. Найти разность фаз колебаний в этих точках.

1) Δφ= ; 2) Δφ= ; 3) Δφ= .

176. Определить скорость v распространения волн в упругой среде, если разность фаз Δφ колебаний двух точек, отстоящих друг от друга на Δx=15 см, равна /2. Частота колебаний .

1) 28 м/с; 2) 51 м/с; 3) 61 м/с.

177. Поперечная волна распространяется вдоль упругого шнура со скоростью v=15 м/с. Период колебаний точек шнура Т=1.2 с. Определить разность фаз Δφ колебаний двух точек, отстоящих от источника волн на расстояниях x₁=20 м и x₂ = =30 м.

1) 1.11; 2) 200⁰; 3) Оба ответа верны.

178. Система массой m совершает вынужденные колебания под действием внешней периодически действующей силы . Внутри системы действуют казиупругая сила и сила сопротивления . Составить дифференциальное уравнение вынужденных колебаний, если m=20 г, F₀=2H, k=100 Н/м, r= 80 Н·с/м.

1) :

2) :

3) .

179. Система массой m совершает вынужденные колебания под действием внешней периодически действующей силы . Внутри системы действуют казиупругая сила и сила сопротивления . Составить дифференциальное уравнение вынужденных колебаний, если m=10 г, F₀=2H, k=100 Н/м, r= 80 Н·с/м.

1) :

2) :

3) .

180. Система массой m совершает вынужденные колебания под действием внешней периодически действующей силы . Внутри системы действуют казиупругая сила и сила сопротивления . Составить дифференциальное уравнение вынужденных колебаний, если m=15 г, F₀=2H, k=100 Н/м, r= 70 Н·с/м.

1) :

2) :

3) .

181. Система массой m совершает вынужденные колебания под действием внешней периодически действующей силы . Внутри системы действуют казиупругая сила и сила сопротивления . Найти резонансную частоту, если k=100 Н/м, r= 0.8 Н·с/м, m=10 г. Справка: резонансная частота рассчитывается по формуле .

1) 82 с^-1; 2) 72 с^-1; 3) 62 с^-1.

181. Система массой m совершает вынужденные колебания под действием внешней периодически действующей силы . Внутри системы действуют казиупругая сила и сила сопротивления . Найти резонансную частоту, если k=100 Н/м, r= 0.9 Н·с/м, m=10 г. Справка: резонансная частота рассчитывается по формуле .

1) 72.6 с^-1; 2) 82.6 с^-1; 3) 62.6 с^-1.

182. Система массой m совершает вынужденные колебания под действием внешней периодически действующей силы . Внутри системы действуют казиупругая сила и сила сопротивления . Найти резонансную частоту, если k=100 Н/м, r= 0.7 Н·с/м, m=10 г. Справка: резонансная частота рассчитывается по формуле .

1) 49.6 с^-1; 2) 39.6 с^-1; 3) 49.5 с^-1.

183. Система массой m совершает вынужденные колебания под действием внешней периодически действующей силы . Внутри системы действуют казиупругая сила и сила сопротивления . Будет ли наблюдаться резонанс, если k=100 Н/м, r= 0.7 Н·с/м, m=10 г.

1) да; 2) нет; 3) будет, если k=0.

184. Система массой m совершает вынужденные колебания под действием внешней периодически действующей силы . Внутри системы действуют казиупругая сила и сила сопротивления . Будет ли наблюдаться резонанс, если k=100 Н/м, r= 7 Н·с/м, m=10 г.

1) да; 2) нет; 3) будет, если k=0.

185. В общем случае изменение частоты звуковых волн в эффекте Доплера определяется формулой: . Какую частоту зарегистрирует неподвижный приемник, если источник приближается к нему со скоростью 50 м/с? Скорость звука в воздухе принять равной 340 м/с.

186. В общем случае изменение частоты звуковых волн в эффекте Доплера определяется формулой: . Какую частоту зарегистрирует неподвижный приемник, если источник удаляется от него со скоростью 50 м/с? Скорость звука в воздухе принять равной 340 м/с.

187. В общем случае изменение частоты звуковых волн в эффекте Доплера определяется формулой: . Какую частоту зарегистрирует приемник, если он приближается к источнику со скоростью 50 м/с? Скорость звука в воздухе принять равной 340 м/с.

188. В общем случае изменение частоты звуковых волн в эффекте Доплера определяется формулой: . Какую частоту зарегистрирует приемник, если он удаляется от источника со скоростью 50 м/с? Скорость звука в воздухе принять равной 340 м/с.

189. Система массой m совершает вынужденные колебания под действием внешней периодически действующей силы . Внутри системы действуют казиупругая сила и сила сопротивления , где k=100 Н/м, r= 0.7 Н·с/м., m=10 г, = 50 с^-1. Чему равна начальная фаза вынужденных колебаний? Справка: начальная фаза вынужденных колебаний находится по формуле .

190. Система массой m совершает вынужденные колебания под действием внешней периодически действующей силы . Внутри системы действуют казиупругая сила и сила сопротивления , где k=100 Н/м, r= 0.6 Н·с/м., m=10 г, = 50 с^-1. Чему равна начальная фаза вынужденных колебаний? Справка: начальная фаза вынужденных колебаний находится по формуле .

191. Электропоезд проходит мимо неподвижного приёмника и даёт гудок, частота которого 300 Гц. Принимая скорость звука равной 340 м/с, определите скачок частоты, воспринимаемой приёмником.

1) 34.5 Гц; 2) 44.5 Гц; 3) 54.5 Гц.

192. Две точки находятся от источника колебаний на расстояниях x₁=4 м и x₁=7 м . Период колебаний Т=20 мс и скорость распространения волны равна 300 м/с. Определите разность фаз колебаний этих точек.

1) ; 2) ; 3) .